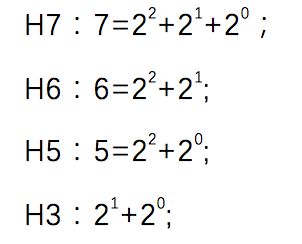海明码的计算方式

      海明码利用奇偶性来检错和纠错的校验方法。海明码的构成方法是在数据位之间的确定位置上插入k个校验位，通过扩大码距来实现检错和纠错。

      设数据位是n位，校验位是k位，则n和k必须满足以下关系： 

      海明码的编码规则如下：

      设有k个校验位Pk,Pk-1,...,P1,n个数据位为Dn-1,Dn-2,...,D1,D0,对应的海明码为Hn+k,Hn+k-1,...,H1,H0,那么：

     （1）P1在海明码的位置，即Hj=Pi,且,数据位则依程序从低到高占据海明码中剩下的位置。

     （2）海明码中任意一位都是由若干个校验码来检验的，其对应关系如下：被校验的海明位的下标等于所有参与校验该位的检验位的下标之和，而校验位由自身校验。

第一种方式：

     对于8位的数据位来说，进行海明码校验需要4个校验位（）。令数据位为D7,D6,D5,D4,D3,D2,D1,D0,校验位为P4,P3,P2,P1,形成的海明码为H12,H11,...,H2,H1,其编码过程如下：

     （1）确定D与P的位置，如下所列：

交错的海明码

H12

H11

H10

H8

H8

H7

H6

H5

H4

H3

H2

H1

位数

D7

D6

D5

D4

D3

D2

D1

D0

信息位

P4

P3

P2

P1

校验位

    （2）确定校验关系，如下表所示：

海明码的校验关系表

海明码	海明码的下标	校验位组	说明（偶校验）
H1(P1)	1	P1	P1校验：P1,D0,D1,D3,D4,D6,即P1=D0^D1^D3^D4^D6
H2(P2)	2	P2	P2校验：P2,D0,D2,D3,D5,D6,即P2=D0^D2^D3^D5^D6
H3(D0)	3=1+2	P1,P2
H4(P3)	4	P3	P3校验：P3,D1D2,D3,D7，即P3=D1^D2^D3^D7
H5(D1)	5=1+4	P1,P3
H6(D2)	6=2+4	P2,P3
H7(D3)	7=1+2+4	P1,P2,P3
H8(P4)	8	P4	P4校验：P4,D4,D5,D6,D7,即P4=D4^D5^D6^D7
H9(D4)	9=1+8	P1,P4
H10(D5)	10=2+8	P2,P4
H11(D6)	11=1+2+8	P1,P2,P4
H12(D7)	12=4+8	P3,P4

     若采用奇校验，则将各校验位的偶校验值取反即可。

   （3）检验错误。对使用海明编码的数据进行差错检测很简单，进行一下计算：

      G1=P1^D0^D1^D3^D4^D6;

      G2=P2^D0^D2^D3^D5^D6;

      G3=P3^D1^D2^D3^D7;

      G4=P4^D4^D5^D6^D7;

      若采用偶校验，则G4G3G2G1全为0时表示接收到的数据无错误（奇校验应全部为1）当G1G2G3G4不全部为0时说明发生了错误，而且G4G3G2G1的十进制值指出了发生错误的位置。例如G4G3G2G1=1010,说明H10(D5)出错了，将其取反即可纠正错误。

第二种方式：

      以实例进行解析，1011的海明码是多少。

      根据上面的公式可以计算，确定校验位位3位，即,其公式表格如下：

H7	H6	H5	H4	H3	H2	H1	位数
D3	D2	D1		D0			信息位
			P3		P2	P1	校验位

H7	H6	H5	H4	H3	H2	H1	位数
1	0	1		1			信息位
			P3		P2	P1	校验位

      说明：P的位置是根据2的n次幂的位置来计算的（P1的位置为，所以位置是H1；P2的位置所以位置是H2；以此类推）。

进行运算：

       说明：因为P1等是根据2的n次幂计算的，所以P1等于所有包含的D值，P2就是等于所有包含的D值，得到如下结果。

P1=D0^D1^D3=1^1^1=1;

P2=D0^D2^D3=1^1^0=0

P3=D1^D2^D3=1^0^1=0

进行校验错误，可以得出P1=1 , P2=0, P3=0。

上述两种方式都可以计算获得海明码，但是第二种方式相对计算快一些。

例题：数据为01101001的海明码，采用4个校验位求其偶校验方式的海明码。

结果：

H12	H11	H10	H9	H8	H7	H6	H5	H4	H3	H2	H1
0	1	1	0		1	0	0		1
				0				1		0	1

以上就是经过一番学习获得收获！