李航统计学习方法之朴素贝叶斯法（含python及tensorflow实现）

朴素贝叶斯法数学表达式

       朴素贝叶斯是一个生成模型。有一个强假设：条件独立性。我们先看下朴素贝叶斯法的思想，然后看下条件独立性具体数学表达式是什么样的。

       条件独立性数学表达式为：

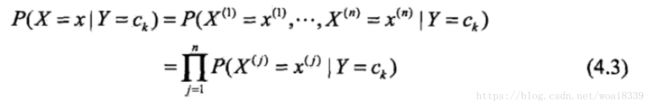
       我们都知道贝叶斯法计算后验概率是依据先验概率和贝叶斯公式得来的，我们有：$$P(Y=y_k|X=x)=\frac{P(X=x|Y=y_k)\ast P(Y=y_k)}{{\sum }_{k}P(X=x|Y=y_k)\ast P(Y=y_k)}(4.4)$$将式(4.3)带入(4.4)中有：
$$P(Y=y_k|X=x)=\frac{P(Y=y_k){\prod }_{j}P(X^{(j)}=x^{(j)}|Y=y_k)}{{\sum }_{k}P(Y=y_k){\prod }_{j}P(X^{(j)}=x^{(j)}|Y=y_k)},k=1,2,...,K(4.5)$$
式(4.5)即为朴素贝叶斯基本公式。朴素贝叶斯分类器可以表示为：
$$y=f(x)=argma{x}_{y_k}\frac{P(Y=y_k){\prod }_{j}P(X^{(j)}=x^{(j)}|Y=y_k)}{{\sum }_{k}P(Y=y_k){\prod }_{j}P(X^{(j)}=x^{(j)}|Y=y_k)},k=1,2,...,K(4.6)$$       注意(4.6)对所有$c_k$都相同，则可以简化为：$$y=f(x)=argma{x}_{y_k}P(Y=y_k)\prod _{j}P(X^{(j)}=x^{(j)}|Y=y_k),k=1,2,...,K(4.7)$$       这里可能会产生一个疑问，为什么是$argmax$化呢，一般我们通常都是最小化风险函数，这个$argmax$和风险函数又有什么关系呢？后验最大化概率的含义又是什么呢？别急，且听慢慢道来。

后验概率最大化的含义

贝叶斯法参数估计

极大似然估计

       我们从贝叶斯目标函数来看，$y=argma{x}_{y_k}{\sum }_{y_k}P(Y=y_k)\ast {\prod }_{j}P(X^{(j)}=x^{(j)}|Y=y_k)$，那么我们需要估计的有两个参数，分别是$P(Y=y_k)$和$P(X^{(j)}=x^{(j)}|Y=y_k)$。
       其中，$P(Y=y_k)$的极大似然概率估计为$$P(Y=y_k)=\frac{{\sum }_{i=1}^{N}I(y_i=y_k)}{N},k=1,2,...,K(4.8)$$
       假设第$j$个特征$x^{(j)}$可能的取值集合为$(a_{j1},a_{j2},...,a_{j{S}_j})$，条件概率$P(X^{(j)}=a_{jl}|Y=y_k)$的极大似然估计是：$$P(X^{(j)}=a_{jl}|Y=y_k)=\frac{{\sum }_{i=1}^{N}I(X_i^{(j)}=a_{jl},Y_i=y_k)}{{\sum }_{i=1}^{N}I(y_i=y_k)}$$$$j=1,2,...,n;l=1,2,...,S_j;k=1,2,...,K$$$式中，x_i^{(j)}是第i个样本第j个特征；a_{jl}是第j个特征可能取的第l个数值；I是指示函数。$

朴素贝叶斯算法思路

       算法思路如下截图所示：

例题代码实现

       我们用李航例题来实现该算法。例题如下：

按算法思路：
1）先计算label概率$P(Y=1)$和$P(Y=-1)$
2）在$Y=1$和$Y=-1$的条件下，分别计算各个特征值的概率
3）计算$P(Y=1)P(X=2|Y=1)P(X=S|Y=1)$和$P(Y=-1)P(X=2|Y=-1)P(X=S|Y=-1)$的概率，取大者。
python代码如下：

import numpy as np

"""
@:param features : 输入的特征，array类型
@:param label : 输入features对应的label，array类型
@:param input: 给定的一组特征，判断属于哪一个类别
"""
def naive_bayes_classifiers(features, label, input_data):
    #计算各个label的概率
    label_category = list(set(label))
    label_number = len(label_category)
    label_prob = {}
    for i in range(0, label_number):
        label_prob[label_category[i]] = len(label[label==label_category[i]])/len(label)
    # print(label_prob) #{1: 0.6, -1: 0.4}

    #2、计算label条件下每一类特征中不同特征取值的条件概率

    len_features = len(features)
    features_set = {}
    #2.1、计算每一类特征里有哪些取值
    for i in range(0,len_features):
        features_set[i] = list(set(features[i]))
    #print(features_set) #{0: ['2', '3', '1'], 1: ['L', 'S', 'M']},表明有两类特征
    #2.2、计算不同label(-1/1)情况下每类特征不同取值的概率P，key为feature+label,
    #比如，01-1表示在Y=-1的情况下第一类特征且取值为1的条件概率P(X0=1|Y=-1)
    #011表示在Y=1的情况下第一类特征且取值为1的条件概率P(X0=1|Y=1)
    features_label_prob = {}
    prob_nums = len(features_set[0])*len(features)*label_number
    # print(prob_nums) # 计算一共多少种条件概率的组合
    for i in range(0, len(features)):
        for j in range(0, len(features_set[i])):
            for k in range(0, label_number):
                label_select = label[label==label_category[k]]
                denominator = len(label_select)
                # print(denominator)
                label_index = np.where(label==label_category[k])
                object_feature = np.array(features[i])[label_index]
                # print(object_feature)
                numberator_value = object_feature[object_feature==features_set[i][j]]
                numberator = len(numberator_value)
                features_label_prob_key = str(i)+str(features_set[i][j])+str(label_category[k])
                features_label_prob[features_label_prob_key] = numberator/denominator
                # print(features_label_prob_key) # 比对key，分子numberator, 分母denominator 没有问题
                # print(numberator)
                # print(denominator)
    # print(features_label_prob)

    #3、计算给定input_data的类别概率
    calc_label_prob = {}
    multi = 1
    for i in range(0, label_number):
        calc_label_prob[label_category[i]] = label_prob[label_category[i]]
        # print(calc_label_prob[label_category[i]])
        for j in range(0, len(input_data)):
            key = str(j)+str(input_data[j])+str(label_category[i])
            # print(key)
            # print(features_label_prob[key])
            multi = multi * features_label_prob[key]
        calc_label_prob[label_category[i]] = calc_label_prob[label_category[i]]*multi
        multi = 1

    # print(calc_label_prob) #{1: 0.02222222222222222, -1: 0.06666666666666667}

    #返回概率最大的label
    output_label = max(calc_label_prob,key=calc_label_prob.get)
    # print(output_label)
    return output_label
if __name__ == '__main__':
    features = [[1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3],
                ['S', 'M', 'M', 'S', 'S', 'S', 'M', 'M', 'L', 'L', 'L', 'M', 'M', 'L', 'L']]
    features = np.array(features)
    label = [-1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1]
    label = np.array(label)
    input_data = np.array([2, 'S'])
    output_label = naive_bayes_classifiers(features, label, input_data)
    print("the output label of input_data is:{}".format(output_label))

贝叶斯估计

相当于加了一个平滑变量。如果考虑贝叶斯估计的话，那么代码又是什么样呢？饿死我了，让我先吃个午饭。。。。
##############我是华丽丽的午饭分割线############

Ref[2-5为markdown写作语法Ref]：
1、李航统计学习方法
2、https://blog.csdn.net/soindy/article/details/50426362
3、https://blog.csdn.net/ly890700/article/details/73131657
4、https://blog.csdn.net/bat67/article/details/72858409
5、https://blog.csdn.net/tearsky253/article/details/78968221