【数据结构与算法】从0-1小白学习之路(入门篇)
1、算法知识入门篇:
数学基础:
对数:幂的逆运算,如果a^x =N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数。(N>0)
幂:2^n,n叫做2的幂次方,如果为2和3分别叫2次方,和立方。
时间复杂度:
若存在函数f(n),使得当n趋近于无穷大时候,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))称为O(f(n)),O为算法的渐进时间复杂度,简称为时间复杂度。由于经常使用大O表示,所以也被称为大O表示法。
n 表示数据规模的大小;f(n) 表示每行代码执行的次数总和因为这是一个公式,所以用 f(n) 来表示。公式中的 O,表示代码的执行时间T(n)与f(n)表达式成正比。
时间复杂度推导原则:
- 如果运行时间是常数量级,则用常数1表示O(1)
- 只保留时间函数中的最高阶项
- 如果最高阶项存在,则省去最高阶项前面的系数
当n取值足够大的时候,O(1)< O(logn) 空间复杂度: 时间与空间的取舍 小结: 2、数据结构基础入门篇 数组 链表 双端链表 块状链表: 块状链表通过使用可变的顺序表的长度和特殊的插入、删除方式,可以达到 块状链表 块状链表是把一个数组中的元素,分成多个数组,每个数组当成一个节点,普通的链表的节点是单个元素,而块状链表的节点是一个数组。它的查询和修改时间复杂度都是O(sqrt(n)) 数组 VS 链表 补充说明: 链表知识点补充: 理解指针或引用的含义: 栈 假设以数组实现,则栈的特性是先进后出LIFO,操作有2个入栈和出栈。时间复杂度为O(1) 思考1:为什么函数调用要用“栈”来保存临时变量呢?用其他数据结构不行吗? 思考2:内存中的堆栈和数据结构堆栈 补充: 队列 队列的应用 双端队列 优先队列 散列表(哈希表)时间复杂度O(1) 警告: 死链生成的前提因素: 伪代码 由于在执行transfer中,虽然new Table是局部变量,但是原先table的Entry链表是共享的。产生问题的根源是Entry的next被并发修改。导致的结果: 1、对象丢失 == JDK8修复办法==: 并发赋值被覆盖。在JDK7源码中createEntry方法中,新添加的元素直接放到slot槽上,是新添加的元素在下次提取时候可以更快的被访问到。如果两个线程同时执行到赋值的时候,一个线程的赋值就会被另外一个赋值覆盖掉。 已遍历区间和迁移,新增元素丢失,被垃圾回收。因为transfer方法在数据非常大的时候非常消耗资源。当前线程迁移过程中,其他线程新增的元素可能落在已经遍历过的哈希槽上。在遍历完成后,table数组引用指向了newTabel,这时候新增的元素就会丢失,被垃圾回收。在迁移过程中,有并发时候,next被提前置成null 新表被覆盖。resize方法完成,执行了table=new Table,则后续元素可以在新表上插入操作。但是多个线程同时resize,以及每个线程都new Entry[new Capacity]。这是线程内部局部数组对象,线程之间不可见。迁移完成之后,resize线程赋值给table共享变量,从而覆盖其他线程的操作。 解决方法:ConcurrentHashMap,Collections.synchronizedMap(),加锁. table-----存储所有节点数据的数组 table的长度64,数据存储结构分为2种,链表和红黑树 JDK8中正是借助baseCount和CounterCells两个属性,并配合多次使用CAS方法,JDK8中的ConcurrentHashMap避免了锁的使用。 3、中级数据结构入门篇 树 树的高度或深度概念: 二叉树 满二叉树 完全二叉树 二叉树的物理存储结构实现 二叉树的应用 对一个节点分布相对均衡的二叉查找树,如果节点总数为n,那么搜索节点的时间复杂度就是O(logn)和树的深度一样。依靠比较大小来逐步查找,类似二分查找算法。 平衡二叉树 AVL树 B-树:多路搜索树,每个结点存储M/2到M个关键字,非叶子结点存储指向关键 B+树:在B-树基础上,为叶子结点增加链表指针,所有关键字都在叶子结点 B*树:在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率 资料补充:B/B+树: 用在磁盘文件组织 数据索引和数据库索引。 红黑树 小结: 红黑树与AVL树区别: Trie树(字典树): 用在统计和排序大量字符串,如自动机 树堆 二叉堆 二叉树的遍历 排序二叉树 查询操作: 优先队列
对一个算法在运行过程中临时占用存储空间大小的量度,同样使用大O表示法。
程序占用空间大小的计算公式记作S(n)=O(f(n))其中n为问题的规模,f(n)为算法所占存储空间的函数。
与时间复杂度计算一样,常量空间为O(1),线性空间比如一维数组,空间复杂度为O(n),二维空间,空间复杂度为O(n^2).递归空间空间复杂度O(n)。
二者不可兼得,根据需要来选择
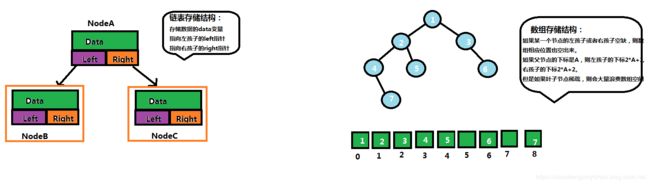
数据结构包含基本数据结构、数组、链表,散列表,栈,队列、双向队列。也包含高级数据结构树、图。
有限个相同类型的变量所组成的有序集合,数组中的每个变量被称为元素,数组是最简单和最常用的数据结构。
数组的特点是:内存中有序排列,这样优点很明显方便查找,但是不方便插入和删除。可以思考下军队站队,如果中间丢掉一个人,后面其他人是需要整体移动,但是由于站好队伍之后,每个人都是按报号排列这样每个人都代表了个数字,查找的时候很方便。
数组的寻址公式(计算出该元素存储的内存地址):
a[i]_address = base_address + i * data_type_size
其中data_type_size表示数组中每个元素的大小。我们举的例子里数组中存储的是int类型数据,所以data_type_size为4个字节。面试的时候容易出错的点:数组和链表的区别:链表适合插入、删除时间复杂度O(1),数组适合随机访问,根据下标随机访问的时间复杂度为O(1).
容器能否完全替代数组?
ArrayList 最大的优势就是可以将很多数组操作的细节封装起来。比如前面提到的数组插入、删除数据时需要搬移其他数据等.另外,它还有一个优势,就是支持动态扩容(扩容1.5倍)。由于扩容的内存申请和数据迁移比较耗时,所以最好是一开始就确定数据大小入参。

为什么大多数编程语言中,数组要从 0 开始编号,而不是从 1?

二维数组内存寻址:
对于 m * n 的数组,a [ i ][ j ] (i < m,j < n)的地址为:
address = base_address + ( i * n + j) * type_size
单向链表,双向链表
链表是一种在物理上非连续,非顺序的数据结构,由若干个节点所组成。
单向链表的每个节点包含两部分,一部分是存放数据的data,一个是存放指向下个节点的指针next
链表的第一个节点被称为头节点,最后一个节点被称为尾节点。



双向链表除了拥有头结点和尾节点,还拥有指向前置节点的prev指针节点。
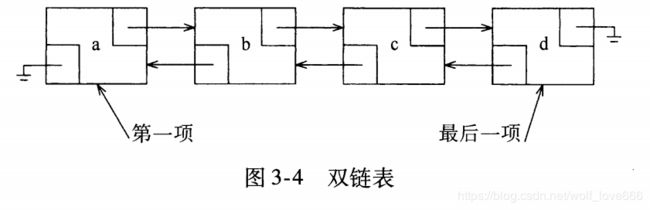
单链表和双链表性能特点:
和单链表相比,存储相同的数据,需要消耗更多的存储空间。
插入、删除操作比单链表效率更高O(1)级别。
对于一个有序链表,双向链表的按值查询效率要比单链表高一些,无序链表时间复杂度都是O(n)
双向循环链表(双向,循环链表的结合)
首节点的前驱指针指向尾节点,尾节点的后继指针指向首节点。双端链表与单链表十分相似,不同的是它新增一个对尾结点的引用。双端链表不是双向链表。
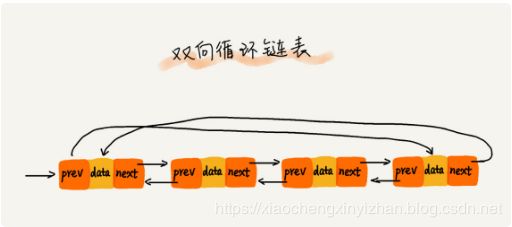
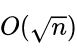 的复杂度。块状链表另一个特点是相对于普通链表来说节省内存,因为不用保存指向每一个数据节点的指针。
的复杂度。块状链表另一个特点是相对于普通链表来说节省内存,因为不用保存指向每一个数据节点的指针。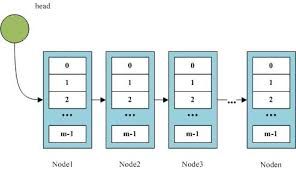
类别
查找
更新
插入
删除
数组
O(1)
O(1)
O(n)
O(n)
链表
O(n)
O(1)
O(n)
O(n)
数组:插入、删除的时间复杂度是O(n),随机访问的时间复杂度是O(1)。
链表:插入、删除的时间复杂度是O(1),随机访问的时间复杂度是O(n)。
数组缺点:
1)若申请内存空间很大,比如100M,但若内存空间没有100M的连续空间时,则会申请失败,尽管内存可用空间超过100M。
2)大小固定,若存储空间不足,需进行扩容,一旦扩容就要进行数据复制,而这时非常费时的。
链表缺点:
1)内存空间消耗更大,因为需要额外的空间存储指针信息。
2)对链表进行频繁的插入和删除操作,会导致频繁的内存申请和释放,容易造成内存碎片,如果是Java语言,还可能会造成频繁的GC(自动垃圾回收器)操作。
如何选择:
数组简单易用,在实现上使用连续的内存空间,可以借助CPU的缓冲机制预读数组中的数据,所以访问效率更高,而链表在内存中并不是连续存储,所以对CPU缓存不友好,没办法预读。
如果代码对内存的使用非常苛刻,那数组就更适合
引申:CPU缓存机制指的是什么?为什么就数组更好了?
CPU在从内存读取数据的时候,会先把读取到的数据加载到CPU的缓存中。而CPU每次从内存读取数据并不是只读取那个特定要访问的地址,而是读取一个数据块并保存到CPU缓存中,然后下次访问内存数据的时候就会先从CPU缓存开始查找,如果找到就不需要再从内存中取。这样就实现了比内存访问速度更快的机制,也就是CPU缓存存在的意义:为了弥补内存访问速度过慢与CPU执行速度快之间的差异而引入。
对于数组来说,存储空间是连续的,所以在加载某个下标的时候可以把以后的几个下标元素也加载到CPU缓存这样执行速度会快于存储空间不连续的链表存储。
将某个变量(对象)赋值给指针(引用),实际上就是就是将这个变量(对象)的地址赋值给指针(引用)。
指针中存储了这个变量的内存地址,指向了这个变量,通过指针就能找到这个变量
示例:
p—>next = q; 表示p节点的后继指针存储了q节点的内存地址。
p—>next = p—>next—>next; 表示p节点的后继指针存储了p节点的下下个节点的内存地址。
由于插入和删除操作都是由指针控制则警惕指针丢失和内存泄漏(单链表)
在插入和删除结点时,要注意先持有后面的结点再操作,否者一旦后面结点的前继指针被断开,就无法再访问,导致内存泄漏。
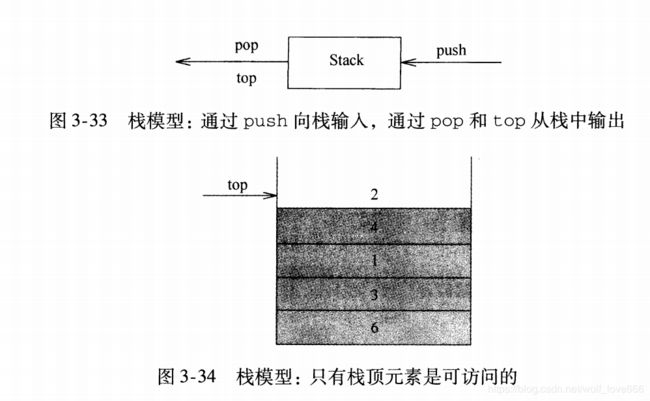
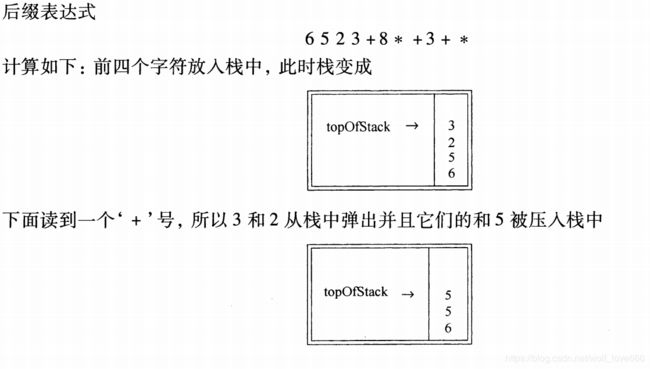
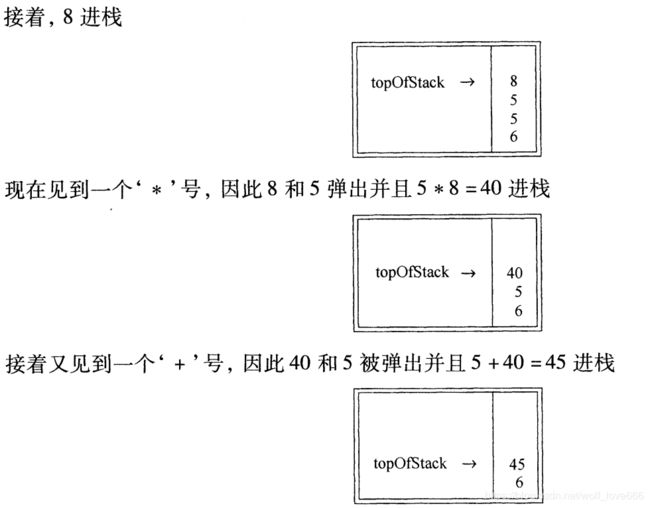
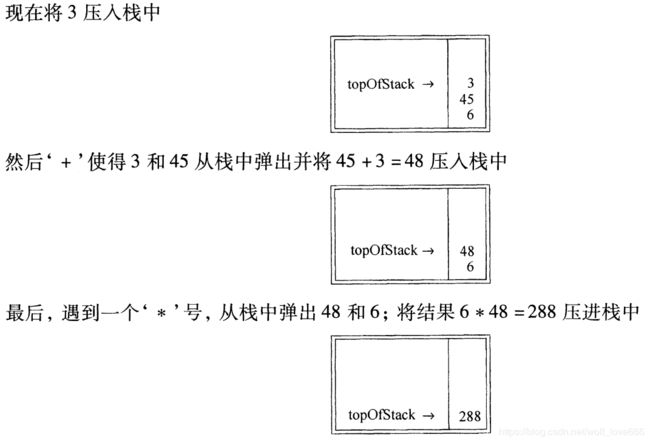

栈的应用:
代码区:存储方法体的二进制代码。高级调度(作业调度)、中级调度(内存调度)、低级调度(进程调度)控制代码区执行代码的切换。
静态数据区:存储全局变量、静态变量、常量,常量包括final修饰的常量和String常量。系统自动分配和回收。
栈区:存储运行方法的形参、局部变量、返回值。由系统自动分配和回收。
堆区:new一个对象的引用或地址存储在栈区,指向该对象存储在堆区中的真实数据。
调试递归:
特性是先进先出,队列的出口端叫做队头,出口端叫做队尾,也包含2个操作,入队和出队。

非常广泛,特别是一些具有某些额外特性的队列,比如循环队列、阻塞队列、并发队列。它们在很多偏底层的系统、框架、中间件的开发中,起着关键性的作用。比如高性能队列 Disruptor、Linux 环形缓存,都用到了循环并发队列;Java concurrent 并发包利用 ArrayBlockingQueue 来实现公平锁等。
关于如何实现无锁并发队列
可以使用 cas + 数组的方式实现。
队列的其他应用
分布式消息队列,如 kafka 也是一种队列。
双端队列综合了栈和队列的优点,对双端队列来说,从队头可以入队和出队,也可以从队尾入队和出队。
基于二叉堆实现,对比谁的优先级高,优先级高的出队。
哈希函数:在Java及大多数面向对象的语言中,每一个对象都有属于自己的hashcode,这个hashcode是区分不同对象的重要标识。无论自身的类型是什么,它们的hashcode都是一个整型变量。
直接定址法:取关键字或关键字的某个线性函数值为散列地址。即h(key) = key,或h(key) = a * key +b,其中a和b为常数。
数字分析法
平方取值法:取关键字平方后的中间几位为散列地址。
折叠法:将关键字分割成位数相同的几部分,然后取这几部分的叠加和作为散列地址。
除留余数法:取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址,即 h(key) = key MOD p ; p<=m;
随机数法:选择个随机函数,取关键字的随机函数值为它的散列地址。h(key) = random(key)
超时价格牌,字典,电话通讯录,网址映射到IP(DNS解析)
当一定长度的数组,哈希函数得到的结果值可能是相同的,这种情况就叫做哈希冲突。
基本思路:判断当前是否有值,如果有值向下移动,依次排除。
在Java中,ThreadLocal所使用的就是开放寻址法。
java中hashMap现在使用的形式,数组的对象是链表。(JDK8+还包括红黑树)
JDK中的散列表实现HashMap的影响因素有两个,一个是Capacity,HashMap的当前长度默认16,一个是LoadFactor,HashMap的负载因子,默认值0.75f。当数组中的元素达到12,则会自动扩容为2倍大小,首先创建一个新的空数据组(长度是原来2倍),遍历原Entry数组,重新hash到新的数组中。
HashMap散列表死链问题(put后扩容,transfer方法是罪魁祸首),JDK8已经修复
原先没有死链的同一个slot上节点遍历一定能够按顺序走完
table数组是各线程都可以共享修改的对象
put/get/transfer三种操作在运行到拥有死链的slot上,CPU使用率都会飙升while(null !=e){
Entry
2、两个对象互链
3、对象自己互链
由于从头节点就开始操作数据迁移,线程A和线程B并发操作导致的同时修改了指针next的指向变量。所以JDK8采用对原先链表的头尾节点引用,保证有序性。
slot------哈希槽。即table【i】这个位置
bucket--------哈希桶。table[i]上所有元素形成的表或树的结合
当某个槽内的元素增加到超过8个且table的容量大于或等于64,由链表转为红黑树。当某个槽内元素个数减少到6个,红黑树重新转回链表。链表转红黑树的过程,就是把给定顺序的元素构成一颗红黑树的过程。需要注意当table容量小于64时候,只会扩容,不会把链表转为红黑树。
转换过程:
用同步块锁住当前槽的首元素,防止其他进程对当前槽进行增删改操作,转换完成后利用CAS替换原有链表。因为TreeNode节点也存储类next引用,所以红黑树转链表的操作就变得简单。只要从TreeBin的first元素开始遍历所有的节点,并把节点从TreeNode类型转化为Node类型。当构造好新的链表,会同样利用CAS替换原有红黑树。

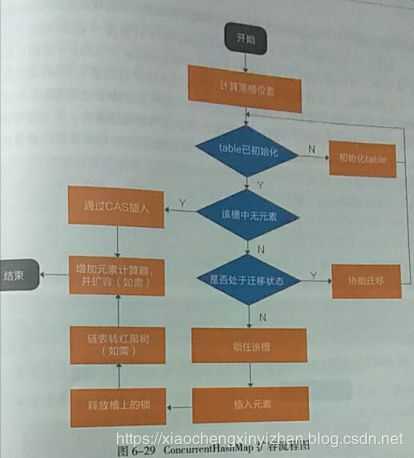
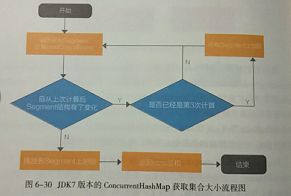
当并发量较小时候,优先使用CAS的方式直接更新baseCount。
当更新baseCount冲突,则会认为进入到比较激励的竞争状态,通过启动counterCells减少竞争。
如果更新counterCells上的某个位置上出现了多次失败,则会通过扩容counterCells的方式减少冲突
当counterCells处在扩容期间内,会尝试更新baseCount值。
而对于元素总数的统计,逻辑就非常简单了。只需要让baseCount加上各种counterCells内的数据,就可以得到哈希内的元素总数,整个过程完全不需要借助锁。
树和图是非线性数据结构,一本书的目录,家谱,企业职级关系都可以用树表示。
树的定义:
树是n(n>=0)个节点的有限集,当n=0时候,称为空树,在任意一个非空树中,有如下特点:
1、有且仅有一个特定的称为根的节点。
2、当n>1时候,其余节点可分为m(m>0)个互不相交的有限集,每一个集合本身又是一个树,并称为根的子树。
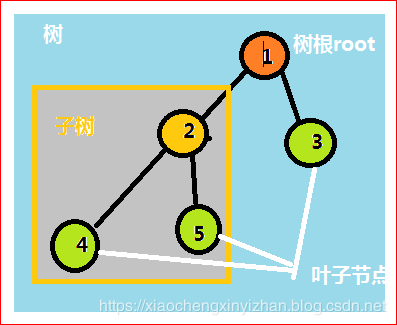
树结构的特点:
树的最大层级数,根据上图我们可以得知我们这个树的高度是3,路径是1-2-4
1叫做树根也叫做根节点,2叫做1的孩子节点,2叫做3的兄弟节点。
二叉树是树的一种特殊形式,二叉的意思是这种树的每个节点最多有2个孩子节点。(可以是没有,也可以是1个孩子节点)
我们上面的那个图就符合二叉树
二叉树的节点的2和3分别叫做左孩子和右孩子。
一个二叉树的所有非叶子节点都存在左右孩子,并且所有叶子节点都在同一层级上,那么这个树就是满二叉树。

如上图所示,我们添加了2个叶子节点6和7这个状态的树我们称为满二叉树。
对一个有n个节点的二叉树,按层级顺序编号,则所有节点的编号从1到n,如果这个树所有节点和同样深度的满二叉树的编号从1到n的节点位置相同,则这个二叉树为完全二叉树。
完全二叉树是满二叉树的特殊一种形态:最后一个节点的之前所有的叶子节点都齐全则符合。

查找操作和维持相对顺序
限制条件:
二叉树的前提下:
引入的问题如果全部为小,或者为大。则变为非平衡状态的二叉树。
以树之名,行链表之实。那么以树的复杂结构实现简单的链表功能,则有点大材小用。
而是否为平衡二叉树,取决于高度差。
平衡二叉树的性质:
1、树的左右高度差不能超过1.==
2、任何往下递归的左子树与右子树必须符合第一条性质
3、没有任何节点的空树或只有根节点的树也是平衡二叉树。
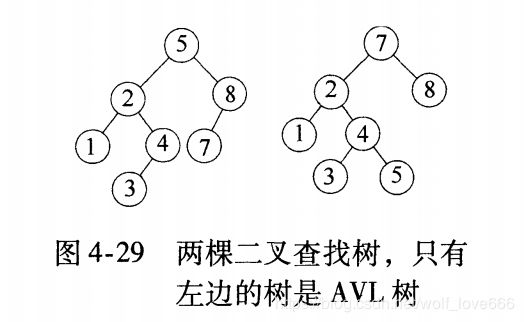
AVL树: 最早的平衡二叉树之一。应用相对其他数据结构比较少。windows对进程地址空间的管理用到了AVL树。
定义:每个节点的左子树和右子树高度最多差1的二叉树,空树的高度定义为-1
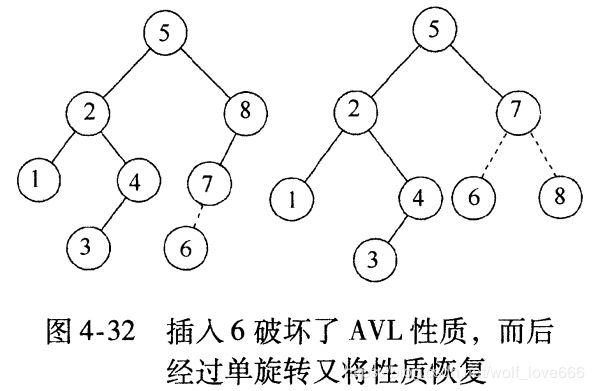
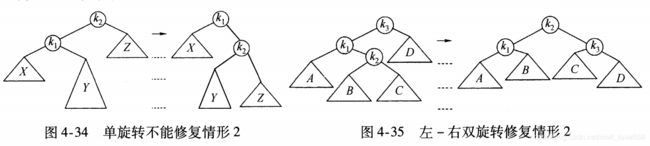
AVL树: 平衡二叉查找树,增加和删除节点后通过树形旋转重新达到平衡。右旋是以某个节点为中心,将它沉入当前右子节点的位置,而让当前的左子节点的位置作为新树的根节点,也称为顺时针旋转。
,同理左旋是以某个节点为中心,将它沉入当前左子节点的位置,而让当前右子节点作为新树的根节点,也称为逆时针旋转。
单旋转
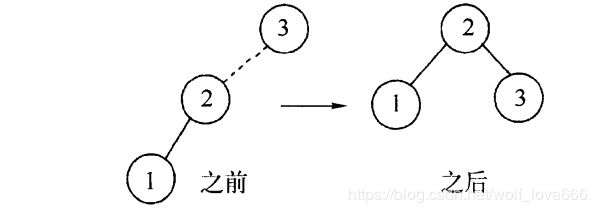
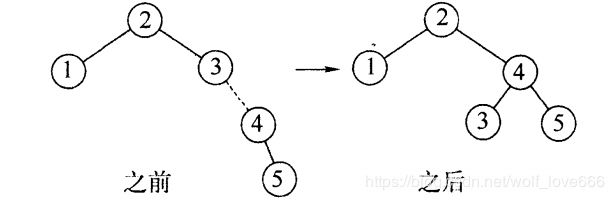
双旋转
B树
B树的非叶子节点存储实际记录的指针, B树:二叉树,每个结点只存储一个关键字,等于则命中,小于走左结点,大于走右结点;
字范围的子结点; 所有关键字在整颗树中出现,且只出现一次,非叶子结点可以命中;
中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中;B+树的叶子节点存储实际记录的指针,B+树的叶子节点通过指针连起来了, 适合扫描区间和顺序查找
从1/2提高到2/3;
平衡二叉树,广泛用在C++的STL中。如map和set都是用红黑树实现的。


红黑树被称为二叉B树、本质还是二叉查找树。
特征:每个节点上增加一个属性来表示节点的颜色,可以是红色也可以是黑色。
红黑树在AVL树的约束条件下,觉得太苛刻了。于是他放宽了下要求:保证从根节点到叶尾的最长路径不超过最短路径的2倍。所以最坏的运行时间是O(log^n)
但是他为了保证自己的特殊:还引入了其他5个特性。
1、节点只能是红色或者黑色
2、根节点必须是黑色
3、所有NIL节点都是黑色(NIL,nothing in leaf即叶子节点不存在的两个虚拟节点,默认是黑色的)
4、一条路径上不能出现两个红色节点
5、在任何递归子树内,根节点到叶子节点的所有路径上包含相同数目的黑色节点。
总结:有红必有黑,红红不相连。红黑树的任何旋转在3次之内均可完成。
先从复杂度分析说起,任意节点的黑深度是指当前节点到NIL途径的黑色节点个数。
在相同节点数的情况下,红黑树的高度可能更高,平均查找次数会高于相同情况下的AVL树。
插入,两者都可以最多两次旋转内恢复平衡。
删除、由于红黑树只追求大致平衡,所以至多三次。而AVL树至多需要O(logn)次旋转。
所以插入和删除选择红黑树,而查找的话选择AVL树。
二叉堆本质是一种完全二叉树,分为两种类型1、最大堆,2、最小堆
最大堆的任何一个父节点的值都大于或者等于它左右孩子的节点值
最小堆的任何一个父节点的值,都小于或者等于它左右孩子的节点的值
二叉堆的根节点叫做堆顶,最大堆的堆顶是整个堆中的最大元素,最小堆的堆顶是整个堆中的最小元素。
先序遍历(前序遍历)根节点-》左子树-》右子树
中序遍历:左子树-》根节点-》右子树
后序遍历:左子树-》右子树-》根节点
前序遍历
若树为空,则空操作返回。否则,先访问根节点,然后前序遍历左子树,再前序遍历右子树。(W)型 (中 左 右)
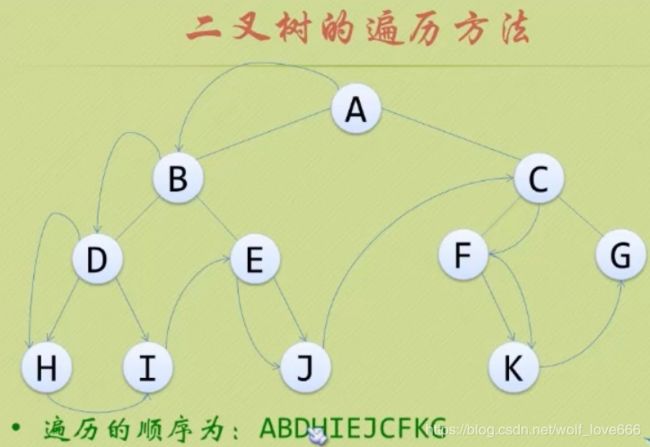
中序遍历
若树为空,则空操作返回。否则,从根节点开始(注意并不是先访问根节点),中序遍历根节点的左子树,然后是访问根节点,最后中序遍历根节点的右子树。(M)型,(左 中 右)
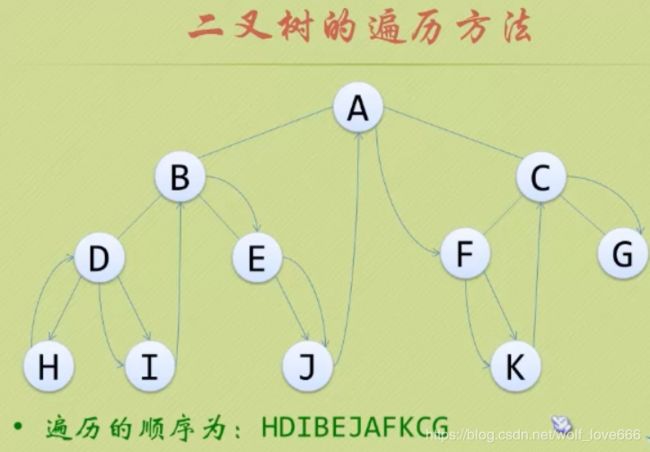
后续遍历
若树为空,则空操作返回。否则,从左到右先叶子后节点的方式遍历访问左右子树,最后访问根节点。(左右中)逆时针型 (左 右 中)

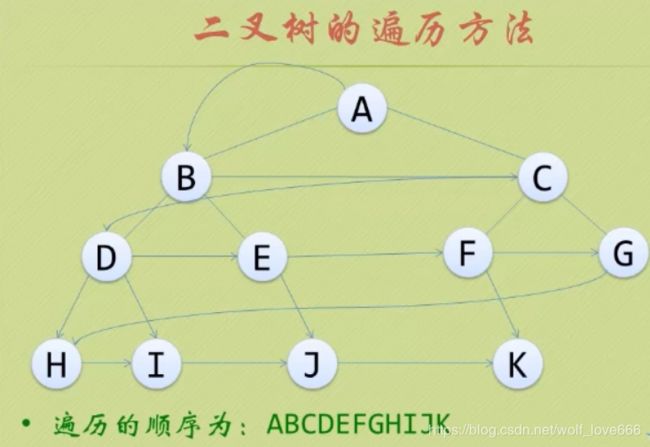
层序遍历
若树为空,则空操作返回。否则,从树的第一层,也就是根节点开始访问,从上到下逐层遍历,在同一层中,按从左到右的顺序结点逐个访问
首先如果普通二叉树每个节点满足:左子树所有节点值小于它的根节点值,且右子树所有节点值大于它的根节点值,则这样的二叉树就是排序二叉树。
插入操作:
首先要从根节点开始往下找到自己要插入的位置(即新节点的父节点);具体流程是:新节点与
当前节点比较,如果相同则表示已经存在且不能再重复插入;如果小于当前节点,则到左子树中 寻找,如果左子树为空则当前节点为要找的父节点,新节点插入到当前节点的左子树即可;如果大于当前节点,则到右子树中寻找,如果右子树为空则当前节点为要找的父节点,新节点插入到当前节点的右子树即可。
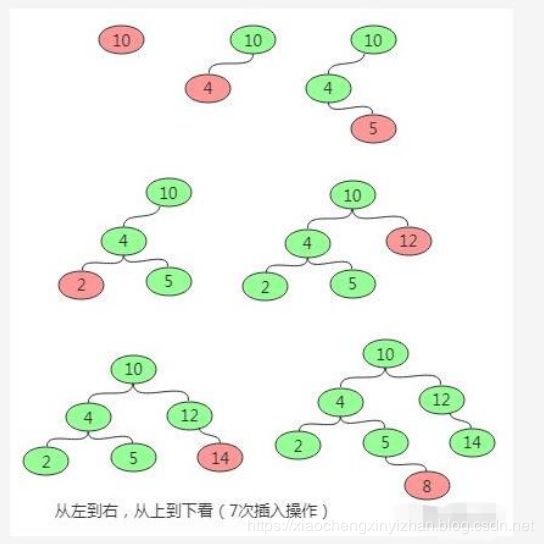
删除操作:
删除操作主要分为三种情况,即要删除的节点无子节点,要删除的节点只有一个子节点,要删除
的节点有两个子节点。

查找操作的主要流程为:先和根节点比较,如果相同就返回,如果小于根节点则到左子树中递归查找,如果大于根节点则到右子树中递归查找。因此在排序二叉树中可以很容易获取最大(最右最深子节点)和最小(最左最深子节点)值。
链表(递归)和栈(非递归)
广度优先遍历:栈实现。