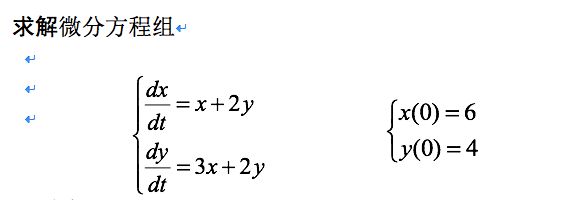C++实现经典四阶龙格库塔法解一阶微分方程

算法原理
用在几个不同点的数值加权平均来代替的值，而使截断误差的阶数尽可能高。我们用四个不同点上的函数值的线性组合，将精度提高到四阶就可以得到四阶龙格-库塔公式。四阶龙格-库塔方法(RK4)可模拟N=4的泰勒方法的精度。这种算法可以描述为，自初始点开始进行计算。

求解微分方程组

//#include 
//#include 
using namespace std;
void RK4(double(*f)(double t, double x, double y), double(*g)(double t, double x, double y), double initial[3], double resu[3], double h)
//定义函数
{
	double f1, f2, f3, f4, g1, g2, g3, g4, t0, x0, y0, x1, y1;
	t0 = initial[0]; x0 = initial[1]; y0 = initial[2];
	f1 = f(t0, x0, y0);                      g1 = g(t0, x0, y0);
	f2 = f(t0 + h / 2, x0 + h*f1 / 2, y0 + h*g1 / 2);   g2 = g(t0 + h / 2, x0 + h*f1 / 2, y0 + h*g1 / 2);
	f3 = f(t0 + h / 2, x0 + h*f2 / 2, y0 + h*g2 / 2);   g3 = g(t0 + h / 2, x0 + h*f2 / 2, y0 + h*g2 / 2);
	f4 = f(t0 + h, x0 + h*f3, y0 + h*g3);         g4 = g(t0 + h, x0 + h*f3, y0 + h*g3);
	x1 = x0 + h*(f1 + 2 * f2 + 2 * f3 + f4) / 6;         y1 = y0 + h*(g1 + 2 * g2 + 2 * g3 + g4) / 6;
	resu[0] = t0 + h; resu[1] = x1; resu[2] = y1;
}
int main()
{
	double f(double t, double x, double y);   //函数申明
	double g(double t, double x, double y);   //函数申明
	double initial[3], resu[3];
	double a, b, H;
	double step;
	int i;
	cout << "输入所求微分方程组的初值t0,x0,y0:";
	cin >> initial[0] >> initial[1] >> initial[2];
	cout << "输入所求微分方程组的微分区间[a,b]:";
	cin >> a >> b;
	cout << "输入所求微分方程组所分解子区间的个数step:";
	cin >> step;
	cout << setiosflags(ios::right) << setiosflags(ios::fixed) << setprecision(10);
	H = (b - a) / step;
	cout << initial[0] << setw(18) << initial[1] << setw(18) << initial[2] << endl;
	for (i = 0; i < step; i++)
	{
		RK4(f, g, initial, resu, H);
		cout << resu[0] << setw(20) << resu[1] << setw(20) << resu[2] << endl;
		initial[0] = resu[0]; initial[1] = resu[1]; initial[2] = resu[2];
	}
	system("pause");
	return(0);
}
//定义微分方程组
double f(double t, double x, double y)    
{
	double dx;
	dx = x + 2 * y;
	return(dx);
}
double g(double t, double x, double y)
{
	double dy;
	dy = 3 * x + 2 * y;
	return(dy);
}