Brian2学习笔记三 Introduction to Brian part 3 :Simulations

1. 前言

推荐几个CSDN上不错的类似教程：
1、链接: https://blog.csdn.net/u013751642/article/details/80947005.
2、链接: https://blog.csdn.net/lemonade_117/article/details/81156087.
3、链接: https://blog.csdn.net/xiaoqu001/article/details/80422546#_Tutorial_84.

本文是根据Brian2官网提供的英文教程进行翻译整理总结的。
Brian2的官方安装教程链接：
链接: https://brian2.readthedocs.io/en/stable/introduction/install.html.
官方文档链接及Jupyter notebook学习资料：
链接: https://brian2.readthedocs.io/en/stable/resources/tutorials/3-intro-to-brian-simulations.html.
（注意：本文所有代码运行环境为Anaconda 的 Spyder（python 3.7）, 注意运行代码首先要通过如下代码来导入 Brian2的包）

因为前段时间一直在改论文，还有中间各种事情，导致这篇学习笔记一直推到了现在，还是要尽快学完的，话不多说，接下来就进入正文部分。

2、正文

如果你还没有读过第一部分神经元和第二部分突触那就先去读吧，然后再来看这篇学习内容。

这一部分的教程是关于在研究问题中出现的稍微复杂的任务，而不是我们目前看到的简单的示例。所以这里包含了输入传感器数据， 模拟实验环境等等。

1、多次运行（Multiple runs）

首先，从一个非常常见的任务开始 : 使用某个参数的变化来进行多次模拟运行。让我们从一些非常简单的任务开始，一个由泊松脉冲神经元驱动的IF神经元的放电速率如何随着神经元膜的时间常数的变化而变化?

from brian2 import* 
# remember, this is here for running separate simulations in the same notebook
start_scope() 
# Parameters
num_inputs = 100
input_rate = 10*Hz
weight = 0.1
# Range of time constants
tau_range = linspace(1, 10, 30)*ms
# Use this list to store output rates
output_rates = []
# Iterate over range of time constants
for tau in tau_range:
    # Construct the network each time
    P = PoissonGroup(num_inputs, rates=input_rate)
    eqs = '''
    dv/dt = -v/tau : 1
    '''
    G = NeuronGroup(1, eqs, threshold='v>1', reset='v=0', method='exact')
    S = Synapses(P, G, on_pre='v += weight')
    S.connect()
    M = SpikeMonitor(G)
    # Run it and store the output firing rate in the list
    run(1*second)
    output_rates.append(M.num_spikes/second)
# And plot it
plot(tau_range/ms, output_rates)
xlabel(r'$\tau$ (ms)')
ylabel('Firing rate (sp/s)')

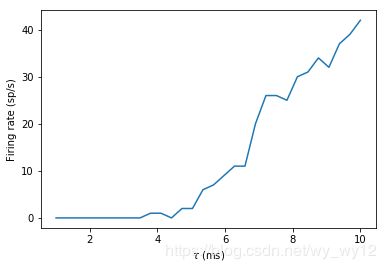
如果你在运行上述代码，你会发现运行速度有点慢。这是因为对于每个循环，都需要重新创建对象。我们可以通过只建立一次网络来改善这一点。我们在循环之前先存储网络状态的副本，并在每次迭代开始时恢复它。

from brian2 import* 
start_scope() 
# Parameters
num_inputs = 100
input_rate = 10*Hz
weight = 0.1
# Range of time constants
tau_range = linspace(1, 10, 30)*ms  #  30 points between 1 and 10
# Use this list to store output rates
output_rates = []
# Construct the network just once
P = PoissonGroup(num_inputs, rates=input_rate)
eqs = '''
dv/dt = -v/tau : 1
'''
G = NeuronGroup(1, eqs, threshold='v>1', reset='v=0', method='exact')
S = Synapses(P, G, on_pre='v += weight')
S.connect()
M = SpikeMonitor(G)  
# Store the current state of the network
store()  
for tau in tau_range:
   # Restore the original state of the network
    restore()
    # Run it with the new value of tau
    run(1*second)
    output_rates.append(M.num_spikes/second)
# And plot it
plot(tau_range/ms, output_rates)
xlabel(r'$\tau$ (ms)')
ylabel('Firing rate (sp/s)')

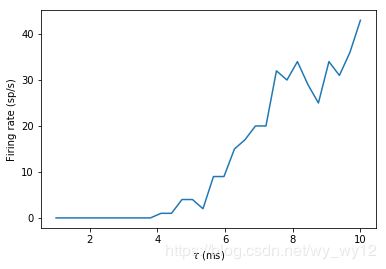
这是一个非常简单的使用存储（store）和恢复（restore）的例子，但是可以在更复杂的情况下使用它。比如，您可能希望运行一个长时间的训练，然后进行多次的测试运行。最简单的方法就是只需在长时间的训练结束之后放置一个存储，并在每次测试运行之前进行恢复。

可以看出输出曲线非常的嘈杂，并不像我们期望的那样单调递增。实际上，这些噪声来自于我们每次重新运行泊松神经元组。如果我们只想看到时间常数的影响，我们可以确保神经元的每次峰值都是相同的(尽管请注意，实际上您应该多次运行并取平均值)。为了方便，我们只运行一次泊松神经元组，然后记录它的峰值，最后再创建一个新的SpikeGeneratorGroup，来记录每次输出的峰值。

from brian2 import *
start_scope() 
num_inputs = 100
input_rate = 10*Hz
weight = 0.1
tau_range = linspace(1, 10, 30)*ms
output_rates = []
# Construct the Poisson spikes just once
P = PoissonGroup(num_inputs, rates=input_rate)
MP = SpikeMonitor(P)
# We use a Network object because later on we don't
# want to include these objects
net = Network(P, MP)
net.run(1*second)
# And keep a copy of those spikes
spikes_i = MP.i
spikes_t = MP.t
# Now construct the network that we run each time
# SpikeGeneratorGroup gets the spikes that we created before
SGG = SpikeGeneratorGroup(num_inputs, spikes_i, spikes_t)
eqs = '''
dv/dt = -v/tau : 1
'''
G = NeuronGroup(1, eqs, threshold='v>1', reset='v=0', method='exact')
S = Synapses(SGG, G, on_pre='v += weight')
S.connect()
M = SpikeMonitor(G)
# Store the current state of the network
net = Network(SGG, G, S, M)
net.store()
for tau in tau_range:
    # Restore the original state of the network
    net.restore()
    # Run it with the new value of tau
    net.run(1*second)
    output_rates.append(M.num_spikes/second)
plot(tau_range/ms, output_rates)
xlabel(r'$\tau$ (ms)')
ylabel('Firing rate (sp/s)')

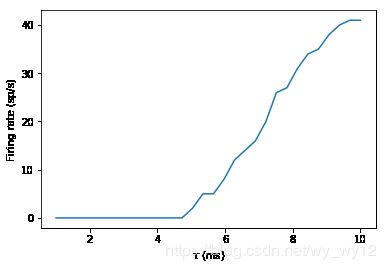
从上面的结果中可以看出，现在的噪声比之更小，是单并且单调递增的。因为每次输入的脉冲都是一样的，这意味着我们看到的是时间常数的作用，而不是随机的脉冲。

请注意，在上面的代码中，我们创建了Network对象。因为在循环中，如果我们只是调用run，它会尝试模拟所有的对象，包括泊松神经元P，但是我们只想运行一次。所以我们使用Network来明确指定我们想要包含的对象。

到目前为止，我们用到的技术只是概念上最简单的多次进行的方法，但它们并不总是最有效的。由于上面的模型中只有一个输出神经元，所以我们可以简单的复制输出神经元并将时间常数设为这个神经元组的一个参数

from brian2 import *
start_scope() 
num_inputs = 100
input_rate = 10*Hz
weight = 0.1
tau_range = linspace(1, 10, 30)*ms
num_tau = len(tau_range)
P = PoissonGroup(num_inputs, rates=input_rate)
# We make tau a parameter of the group
eqs = '''
dv/dt = -v/tau : 1
tau : second
'''
# And we have num_tau output neurons, each with a different tau
G = NeuronGroup(num_tau, eqs, threshold='v>1', reset='v=0', method='exact')
G.tau = tau_range
S = Synapses(P, G, on_pre='v += weight')
S.connect()
M = SpikeMonitor(G)
# Now we can just run once with no loop
run(1*second)
output_rates = M.count/second # firing rate is count/duration
plot(tau_range/ms, output_rates)
xlabel(r'$\tau$ (ms)')
ylabel('Firing rate (sp/s)')

可以看出，这次程序运行的速度快了很多。虽然在概念上更加复杂了，但是如果可以实现的话，它会更加高效。
接下来，我们看一下interspike之间的间隔时间的均值和标准差与时间常数之间的关系。

from brian2 import *
start_scope()
num_inputs = 100
input_rate = 10*Hz
weight = 0.1
tau_range = linspace(1, 10, 30)*ms
num_tau = len(tau_range)
P = PoissonGroup(num_inputs, rates=input_rate)
# We make tau a parameter of the group
eqs = '''
dv/dt = -v/tau : 1
tau : second
'''
# And we have num_tau output neurons, each with a different tau
G = NeuronGroup(num_tau, eqs, threshold='v>1', reset='v=0', method='exact')
G.tau = tau_range
S = Synapses(P, G, on_pre='v += weight')
S.connect()
M = SpikeMonitor(G)
# Now we can just run once with no loop
run(1*second)
output_rates = M.count/second # firing rate is count/duration
 
trains = M.spike_trains()
isi_mu = full(num_tau, nan)*second
isi_std = full(num_tau, nan)*second
for idx in range(num_tau):
    train = diff(trains[idx])
    if len(train)>1:
        isi_mu[idx] = mean(train)
        isi_std[idx] = std(train)
errorbar(tau_range/ms, isi_mu/ms, yerr=isi_std/ms)
xlabel(r'$\tau$ (ms)')
ylabel('Interspike interval (ms)')

注意到这里我们使用SpikeMonitor中的spike_trains()键，这是一个字典，其中键是神经元的索引，值是该神经元的尖峰时间数组。它用于指示对应神经元的spike times组成的数组中的值。

2、在运行期间改变一些内容（Changing things during a run）

想象一个实验，你将电流注入神经元，并每隔10毫秒随机改变幅度会发生什么？ 让我们看看我们是否可以使用Hodgkin-Huxley型神经元对其进行建模。

from brian2 import *
start_scope()
# Parameters
area = 20000*umetre**2
Cm = 1*ufarad*cm**-2 * area
gl = 5e-5*siemens*cm**-2 * area
El = -65*mV
EK = -90*mV
ENa = 50*mV
g_na = 100*msiemens*cm**-2 * area
g_kd = 30*msiemens*cm**-2 * area
VT = -63*mV
# The model
eqs_HH = '''
dv/dt = (gl*(El-v) - g_na*(m*m*m)*h*(v-ENa) - g_kd*(n*n*n*n)*(v-EK) + I)/Cm : volt
dm/dt = 0.32*(mV**-1)*(13.*mV-v+VT)/
    (exp((13.*mV-v+VT)/(4.*mV))-1.)/ms*(1-m)-0.28*(mV**-1)*(v-VT-40.*mV)/
    (exp((v-VT-40.*mV)/(5.*mV))-1.)/ms*m : 1
dn/dt = 0.032*(mV**-1)*(15.*mV-v+VT)/
    (exp((15.*mV-v+VT)/(5.*mV))-1.)/ms*(1.-n)-.5*exp((10.*mV-v+VT)/(40.*mV))/ms*n : 1
dh/dt = 0.128*exp((17.*mV-v+VT)/(18.*mV))/ms*(1.-h)-4./(1+exp((40.*mV-v+VT)/(5.*mV)))/ms*h : 1
I : amp
'''
group = NeuronGroup(1, eqs_HH,
                    threshold='v > -40*mV',
                    refractory='v > -40*mV',
                    method='exponential_euler')
group.v = El
statemon = StateMonitor(group, 'v', record=True)
spikemon = SpikeMonitor(group, variables='v')
figure(figsize=(9, 4))
for l in range(5):
    group.I = rand()*50*nA
    run(10*ms)
    axvline(l*10, ls='--', c='k')
axhline(El/mV, ls='-', c='lightgray', lw=3)
plot(statemon.t/ms, statemon.v[0]/mV, '-b')
plot(spikemon.t/ms, spikemon.v/mV, 'ob')
xlabel('Time (ms)')
ylabel('v (mV)')

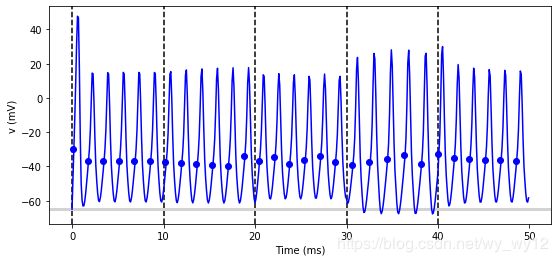
在上面的代码中，我们使用多次循环来实现这个任务。 这虽然没有问题，但并不是最有效的方法，因为每次调用run我们都要做很多初始化工作，这会降低整体的运算速度。 即使是对于Brian这种高效的独立模式，也并没有太大的效果。 接下来我们介绍另一种方法：

from brian2 import *
start_scope()
# Parameters
area = 20000*umetre**2
Cm = 1*ufarad*cm**-2 * area
gl = 5e-5*siemens*cm**-2 * area
El = -65*mV
EK = -90*mV
ENa = 50*mV
g_na = 100*msiemens*cm**-2 * area
g_kd = 30*msiemens*cm**-2 * area
VT = -63*mV
# The model
eqs_HH = '''
dv/dt = (gl*(El-v) - g_na*(m*m*m)*h*(v-ENa) - g_kd*(n*n*n*n)*(v-EK) + I)/Cm : volt
dm/dt = 0.32*(mV**-1)*(13.*mV-v+VT)/
    (exp((13.*mV-v+VT)/(4.*mV))-1.)/ms*(1-m)-0.28*(mV**-1)*(v-VT-40.*mV)/
    (exp((v-VT-40.*mV)/(5.*mV))-1.)/ms*m : 1
dn/dt = 0.032*(mV**-1)*(15.*mV-v+VT)/
    (exp((15.*mV-v+VT)/(5.*mV))-1.)/ms*(1.-n)-.5*exp((10.*mV-v+VT)/(40.*mV))/ms*n : 1
dh/dt = 0.128*exp((17.*mV-v+VT)/(18.*mV))/ms*(1.-h)-4./(1+exp((40.*mV-v+VT)/(5.*mV)))/ms*h : 1
I : amp
'''
group = NeuronGroup(1, eqs_HH,
                    threshold='v > -40*mV',
                    refractory='v > -40*mV',
                    method='exponential_euler')
group.v = El
statemon = StateMonitor(group, 'v', record=True)
spikemon = SpikeMonitor(group, variables='v')
# we replace the loop with a run_regularly
group.run_regularly('I = rand()*50*nA', dt=10*ms)
run(50*ms)
figure(figsize=(9, 4))
# we keep the loop just to draw the vertical lines
for l in range(5):
    axvline(l*10, ls='--', c='k')
axhline(El/mV, ls='-', c='lightgray', lw=3)
plot(statemon.t/ms, statemon.v[0]/mV, '-b')
plot(spikemon.t/ms, spikemon.v/mV, 'ob')
xlabel('Time (ms)')
ylabel('v (mV)')

我们已经用run_regularly替换了之前具有多个run的调用的循环。 这使得指定的代码块每dt = 10 * ms运行一次。 run_regularly允许您运行特定于单个NeuronGroup的代码，但有时可能需要更灵活的方式。 为此，您可以使用network_operation来运行任意Python代码（但不适用于standalone模式）。

from brian2 import *
start_scope()
# Parameters
area = 20000*umetre**2
Cm = 1*ufarad*cm**-2 * area
gl = 5e-5*siemens*cm**-2 * area
El = -65*mV
EK = -90*mV
ENa = 50*mV
g_na = 100*msiemens*cm**-2 * area
g_kd = 30*msiemens*cm**-2 * area
VT = -63*mV
# The model
eqs_HH = '''
dv/dt = (gl*(El-v) - g_na*(m*m*m)*h*(v-ENa) - g_kd*(n*n*n*n)*(v-EK) + I)/Cm : volt
dm/dt = 0.32*(mV**-1)*(13.*mV-v+VT)/
    (exp((13.*mV-v+VT)/(4.*mV))-1.)/ms*(1-m)-0.28*(mV**-1)*(v-VT-40.*mV)/
    (exp((v-VT-40.*mV)/(5.*mV))-1.)/ms*m : 1
dn/dt = 0.032*(mV**-1)*(15.*mV-v+VT)/
    (exp((15.*mV-v+VT)/(5.*mV))-1.)/ms*(1.-n)-.5*exp((10.*mV-v+VT)/(40.*mV))/ms*n : 1
dh/dt = 0.128*exp((17.*mV-v+VT)/(18.*mV))/ms*(1.-h)-4./(1+exp((40.*mV-v+VT)/(5.*mV)))/ms*h : 1
I : amp
'''
group = NeuronGroup(1, eqs_HH,
                    threshold='v > -40*mV',
                    refractory='v > -40*mV',
                    method='exponential_euler')
group.v = El
statemon = StateMonitor(group, 'v', record=True)
spikemon = SpikeMonitor(group, variables='v')
# we replace the loop with a network_operation
@network_operation(dt=10*ms)
def change_I():
    group.I = rand()*50*nA
run(50*ms)
figure(figsize=(9, 4))
for l in range(5):
    axvline(l*10, ls='--', c='k')
axhline(El/mV, ls='-', c='lightgray', lw=3)
plot(statemon.t/ms, statemon.v[0]/mV, '-b')
plot(spikemon.t/ms, spikemon.v/mV, 'ob')
xlabel('Time (ms)')
ylabel('v (mV)')

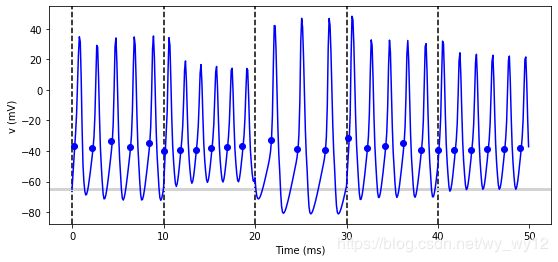
现在，我么扩展这个例子，把它运行在多个神经元上，每个神经元都有不同的电容c用以观察它是如何影响细胞的行为。

from brian2 import *
start_scope()
# Parameters
area = 20000*umetre**2
Cm = 1*ufarad*cm**-2 * area
gl = 5e-5*siemens*cm**-2 * area
El = -65*mV
EK = -90*mV
ENa = 50*mV
g_na = 100*msiemens*cm**-2 * area
g_kd = 30*msiemens*cm**-2 * area
VT = -63*mV
N = 3
# The model
eqs_HH_2 = '''
dv/dt = (gl*(El-v) - g_na*(m*m*m)*h*(v-ENa) - g_kd*(n*n*n*n)*(v-EK) + I)/C : volt
dm/dt = 0.32*(mV**-1)*(13.*mV-v+VT)/
    (exp((13.*mV-v+VT)/(4.*mV))-1.)/ms*(1-m)-0.28*(mV**-1)*(v-VT-40.*mV)/
    (exp((v-VT-40.*mV)/(5.*mV))-1.)/ms*m : 1
dn/dt = 0.032*(mV**-1)*(15.*mV-v+VT)/
    (exp((15.*mV-v+VT)/(5.*mV))-1.)/ms*(1.-n)-.5*exp((10.*mV-v+VT)/(40.*mV))/ms*n : 1
dh/dt = 0.128*exp((17.*mV-v+VT)/(18.*mV))/ms*(1.-h)-4./(1+exp((40.*mV-v+VT)/(5.*mV)))/ms*h : 1
I : amp
C : farad
'''
group = NeuronGroup(N, eqs_HH_2,
                    threshold='v > -40*mV',
                    refractory='v > -40*mV',
                    method='exponential_euler')
group.v = El
# initialise with some different capacitances
group.C = array([0.8, 1, 1.2])*ufarad*cm**-2*area
statemon = StateMonitor(group, variables=True, record=True)
# we go back to run_regularly
group.run_regularly('I = rand()*50*nA', dt=10*ms)
run(50*ms)
figure(figsize=(9, 4))
for l in range(5):
    axvline(l*10, ls='--', c='k')
axhline(El/mV, ls='-', c='lightgray', lw=3)
plot(statemon.t/ms, statemon.v.T/mV, '-')
xlabel('Time (ms)')
ylabel('v (mV)')

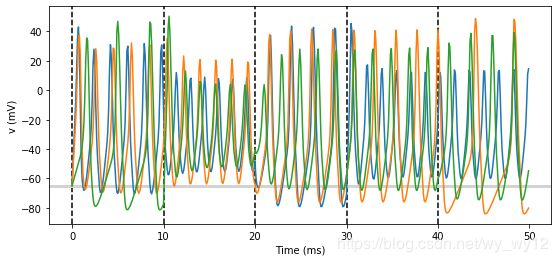
但是，结果好像有些不太对，我们对所有不同的神经元它们的输入电流都是不同的。让我们检查一下，执行如下代码

plot(statemon.t/ms, statemon.I.T/nA, '-')
xlabel('Time (ms)')
ylabel('I (nA)')

从结果中可以看出，每次都是不同的。但是为什么呢？group.run_regularly(I =rand()50nA’, dt=10*ms)似乎应该给每个神经元赋予相同的值。但是，实际上每一个神经元运行run_regularly时，都会单独地运行，而I是参数，因此对于每个神经元是不同的。要想解决这个问题，只需要将I变成一个共享变量，也就是说它对每个神经元都有相同的值。

from brian2 import *
start_scope()
# Parameters
area = 20000*umetre**2
Cm = 1*ufarad*cm**-2 * area
gl = 5e-5*siemens*cm**-2 * area
El = -65*mV
EK = -90*mV
ENa = 50*mV
g_na = 100*msiemens*cm**-2 * area
g_kd = 30*msiemens*cm**-2 * area
VT = -63*mV
N = 3
# The model
eqs_HH_3 = '''
dv/dt = (gl*(El-v) - g_na*(m*m*m)*h*(v-ENa) - g_kd*(n*n*n*n)*(v-EK) + I)/C : volt
dm/dt = 0.32*(mV**-1)*(13.*mV-v+VT)/
    (exp((13.*mV-v+VT)/(4.*mV))-1.)/ms*(1-m)-0.28*(mV**-1)*(v-VT-40.*mV)/
    (exp((v-VT-40.*mV)/(5.*mV))-1.)/ms*m : 1
dn/dt = 0.032*(mV**-1)*(15.*mV-v+VT)/
    (exp((15.*mV-v+VT)/(5.*mV))-1.)/ms*(1.-n)-.5*exp((10.*mV-v+VT)/(40.*mV))/ms*n : 1
dh/dt = 0.128*exp((17.*mV-v+VT)/(18.*mV))/ms*(1.-h)-4./(1+exp((40.*mV-v+VT)/(5.*mV)))/ms*h : 1
I : amp (shared) # everything is the same except we've added this shared
C : farad
'''
group = NeuronGroup(N, eqs_HH_3,
                    threshold='v > -40*mV',
                    refractory='v > -40*mV',
                    method='exponential_euler')
group.v = El
group.C = array([0.8, 1, 1.2])*ufarad*cm**-2*area
statemon = StateMonitor(group, 'v', record=True)
group.run_regularly('I = rand()*50*nA', dt=10*ms)
run(50*ms)
figure(figsize=(9, 4))
for l in range(5):
    axvline(l*10, ls='--', c='k')
axhline(El/mV, ls='-', c='lightgray', lw=3)
plot(statemon.t/ms, statemon.v.T/mV, '-')
xlabel('Time (ms)')
ylabel('v (mV)')

好了，这次运行结果就没有问题了！

3、添加输入（Adding input）

现在我们来考虑一个由正弦输入驱动的神经元。神经元模型使用LIF模型来简化方程。

from brian2 import *
start_scope()
A = 2.5
f = 10*Hz
tau = 5*ms
eqs = '''
dv/dt = (I-v)/tau : 1
I = A*sin(2*pi*f*t) : 1
'''
G = NeuronGroup(1, eqs, threshold='v>1', reset='v=0', method='euler')
M = StateMonitor(G, variables=True, record=True)
run(200*ms)
plot(M.t/ms, M.v[0], label='v')
plot(M.t/ms, M.I[0], label='I')
xlabel('Time (ms)')
ylabel('v')
legend(loc='best')

到目前为止，我们第一次在教程中看到了这么好的东西。 现在，如果输入电流是我们记录并保存在文件中的内容应该怎么办？ 在这种情况下，我们可以使用TimedArray。 让我们使用TimedArray来重新实现上面的任务：

from brian2 import *
start_scope()
A = 2.5
f = 10*Hz
tau = 5*ms
# Create a TimedArray and set the equations to use it
t_recorded = arange(int(200*ms/defaultclock.dt))*defaultclock.dt
I_recorded = TimedArray(A*sin(2*pi*f*t_recorded), dt=defaultclock.dt)
eqs = '''
dv/dt = (I-v)/tau : 1
I = I_recorded(t) : 1
'''
G = NeuronGroup(1, eqs, threshold='v>1', reset='v=0', method='exact')
M = StateMonitor(G, variables=True, record=True)
run(200*ms)
plot(M.t/ms, M.v[0], label='v')
plot(M.t/ms, M.I[0], label='I')
xlabel('Time (ms)')
ylabel('v')
legend(loc='best')

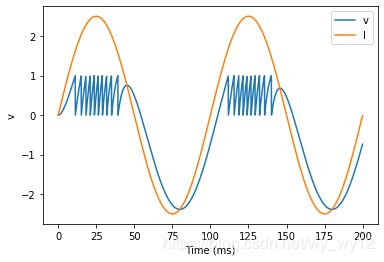
请注意，我们将sin函数直接加入方程中，我们必须使用method ='euler’参数，因为exact积分器在这里不起作用（你可以自己试试吧！）。 但是，TimedArray被认为在时间步长上是恒定的，因此可以使用线性积分器。 这意味着由于以下两个原因，您将不会从这两种方法中获得相同的行为。 首先，exact和euler方法的结果会略有不同。 其次，sin在时间步长上不是恒定的，而TimedArray则是。
现在只是为了表明TimedArray适用于任意电流，让我们随意制作一个比较奇怪的“recorded”电流并运行它。

from brian2 import *
start_scope()
A = 2.5
f = 10*Hz
tau = 5*ms
# Let's create an array that couldn't be
# reproduced with a formula
num_samples = int(200*ms/defaultclock.dt)
I_arr = zeros(num_samples)
for _ in range(100):
    a = randint(num_samples)
    I_arr[a:a+100] = rand()
I_recorded = TimedArray(A*I_arr, dt=defaultclock.dt)
eqs = '''
dv/dt = (I-v)/tau : 1
I = I_recorded(t) : 1
'''
G = NeuronGroup(1, eqs, threshold='v>1', reset='v=0', method='exact')
M = StateMonitor(G, variables=True, record=True)
run(200*ms)
plot(M.t/ms, M.v[0], label='v')
plot(M.t/ms, M.I[0], label='I')
xlabel('Time (ms)')
ylabel('v')
legend(loc='best')

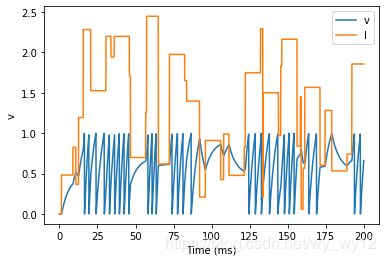
最后，让我们完成一个从文件中实际读取数据的示例。看看你能不能明白这个例子是如何工作的？

from brian2 import *
start_scope()
from matplotlib.image import imread
img = (1-imread('brian.png'))[::-1, :, 0].T
num_samples, N = img.shape
ta = TimedArray(img, dt=1*ms) # 228
A = 1.5
tau = 2*ms
eqs = '''
dv/dt = (A*ta(t, i)-v)/tau+0.8*xi*tau**-0.5 : 1
'''
G = NeuronGroup(N, eqs, threshold='v>1', reset='v=0', method='euler')
M = SpikeMonitor(G)
run(num_samples*ms)
plot(M.t/ms, M.i, '.k', ms=3)
xlim(0, num_samples)
ylim(0, N)
xlabel('Time (ms)')
ylabel('Neuron index')

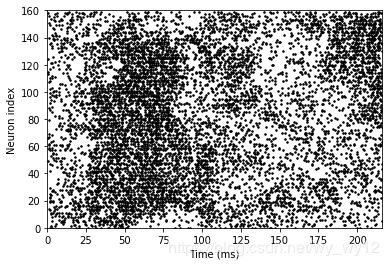
注意，读入的图片文件格式为8bit灰度图像，且图像尺寸不能过大，下图为输入图像，上图为程序运行结果图。

3、总结

虽然时隔快两周了，才把这个学习教程写完，不顾感觉还是提升很多，在翻译和程序运行过程中，虽有些问题，不过都逐渐解决了，环境配置和github的官方文档也很值得学习，接下来会学习一下官方的examples, 另外再结合一些文章和代码来实践练习，欢迎大家来交流！