数据结构 —— B树

1、B树的定义

B-tree 即 B树，B 即 Balanced，平衡的意思。

B树 是一颗多路平衡查找树。

B 树又叫平衡多路查找树。一棵m阶的B 树 (m叉树)的特性如下：

1. 根节点至少有两个孩子 。
2. 每个非根节点至少有M/2（上取整）个孩子，至多有M个孩子。
3. 每个叶子节点 至少有 M/2-1（上取整）个关键字，至多有 M-1 个关键字。并以升序排列。（注：叶子节点是没有孩子）
4. key[i] 和 key[i+1] 之间的孩子节点的值介于 key[i] 和 key[i+1] 之间。
5. 所有的叶子节点都在同一层。

1.1、B树的特性

一棵m阶B树（m>=3），或是空树，或是具有如下几个特征的树：

1. 如果是根结点，则 2 <= 根结点的孩子数 <= m；（根结点至少包含一个关键字）。
2. 非叶子节点（除根结点和叶子结点外），ceil(m/2) <= 其包含的孩子数 <= m，其包含的关键字数 = 它的孩子数-1。【注：ceil(x)：向上取整】
3. 所有叶子结点都出现在同一层，ceil(m/2)-1 <= 结点包含的 关键字数 <= m - 1；
4. 每个结点中的 关键字 从小到大排列，并且非叶子结点的k-1个 关键字 ，正好是它k个孩子包含的关键字的值域分划。
   【即：父结点中的第i个关键字（如果存在） < 第i个孩子中的所有关键字 < 父结点中的第i+1个关键字（如果存在）】

1.2、B树的高度

对于一个m（m>=3）阶B树，假设关键字总数目为n，高度为h：

1. 根结点至少有2个孩子（根结点至少有一个关键字），因此第二层至少有两个结点；
2. 除根和叶子结点外，其他结点至少有t=ceil(m/2)个孩子（取最小时，除根结点外，其他结点包含的关键字个数为t-1）。因此，第三层至少有2t个结点（第二层每个结点包含的关键字个数为t-1），第四层至少有 2t^2 个结点（第三层每个结点包含的关键字个数为t-1），……，第h-1层至少有2t^(h-3)个结点（第h-2层每个结点包含的关键字个数为t-1）；
3. 将所有结点包含的关键字相加：

由此可知：

1. 在B树上增删改查的磁盘IO次数为为O(logtn)，CPU时间为O(mlogtn)。
2. 在关键字总数目不变的情况下，结点包含的关键字越多，B树的高度越小。这也是为什么SQL Server中应尽量以窄键建立聚集索引。因为键越小，结点可容纳的关键字越多，B树的高度越小，从而提升了查询性能。

1.3、性能分析

1. n个关键字的平衡二叉排序的高度（lgn）比B树的高度约大lgt倍。

2. 若作为在内存中使用的表结构，B树不一定比平衡二叉树好，尤其当m较大时更是如此。
   这是因为B树增删改查的CPU时间：O(mlogtn)=0(lgn·(m/lgt))。

   而m/lgt>1，因此当m较大时，O(mlogtn)比平衡二叉排序树的CPU时间O(lgn)大得多。故，若B树仅作为在内存中使用，则应取较小的m。（通常取最小值m=3，此时B树每个内部结点孩子数目可为2或3，这种3阶的B-树称为2-3树）。

1.4、B树的补充说明

1. B树的 阶数 是指 树中 的 最多子节点个数。比如，2-3树的阶是3，2-3-4树的阶是4；
2. B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点；
3. 关键字集合分布在整棵树中, 即叶子节点和非叶子节点都存放数据；
4. 搜索有可能在非叶子结点结束；
5. 其搜索性能等价于在关键字全集内做一次二分查找；

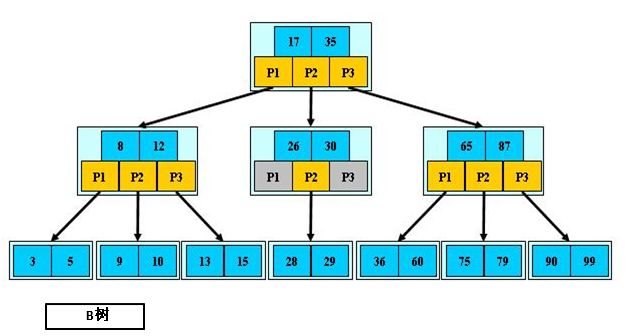
上图是一颗阶数为4的B树。

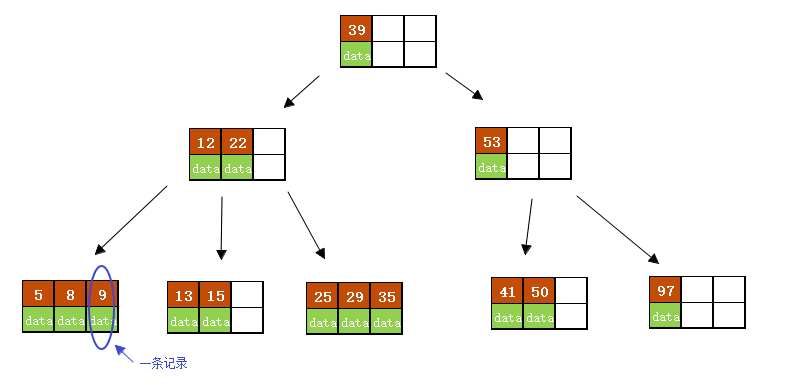
在实际应用中的B树的阶数m都非常大（通常大于100），所以即使存储大量的数据，B树的高度仍然比较小。每个结点中存储了关键字（key）和关键字对应的数据（data），以及孩子结点的指针。

我们将一个key和其对应的data称为一个记录。但为了方便描述，除非特别说明，后续文中就用key来代替（key, value）键值对这个整体。在数据库中我们将B树（和B+树）作为索引结构，可以加快查询速速，此时B树中的key就表示键，而data表示了这个键对应的条目在硬盘上的逻辑地址。

1.5 、B树、B-树 、B-tree、B tree的区别

1. B树： B树 的原英文名称为 B-tree 。

2. B-树：国内很多人喜欢把 B-tree 译作 B-树 。其实，这是个非常不好的直译，很容易让人产生误解。 初学者可能误认为 B-树 是一种树，而 B树 又是另一种树。 而事实上是 它们都是指的同一种 “树” 。

3. B tree ： 就是 B树 。

总结： B树 == B-树 == B-tree == B tree 。

2、B树的插入操作

插入操作是指插入一条记录，即（key, value）的键值对。如果B树中已存在需要插入的键值对，则用需要插入的value替换旧的value。若B树不存在这个key,则一定是在叶子结点中进行插入操作。

1）根据要插入的key的值，找到叶子结点并插入。

2）判断当前结点key的个数是否小于等于m-1，若满足则结束，否则进行第3步。

3）以结点中间的key为中心分裂成左右两部分，然后将这个中间的key插入到父结点中，这个key的左子树指向分裂后的左半部分，这个key的右子支指向分裂后的右半部分，然后将当前结点指向父结点，继续进行第3步。（ 当阶数m为偶数时，需要分裂时就不存在排序恰好在中间的key，那么我们选择中间位置的前一个key或中间位置的后一个key为中心进行分裂即可。 ）

下面以5阶B树为例，介绍B树的插入操作，

根B定义规则2（ 至少有Math.ceil(m/2)-1个关键字 ），在5阶B树中，结点最多有4个key，最少有2个key。

---

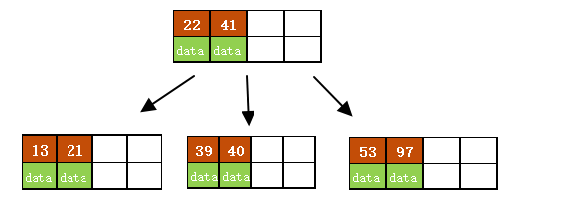
a）在空树中插入39

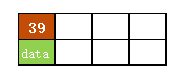
此时根结点就一个key，此时根结点也是叶子结点

---

b）继续插入22、97、41

根结点此时有4个key

---

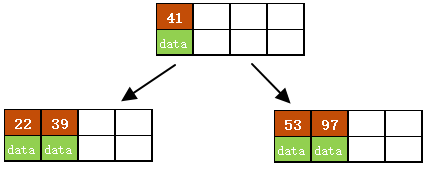
c）继续插入53

插入后超过了最大允许的关键字个数4，所以以key值为41为中心进行分裂，结果如下图所示，分裂后当前结点指针指向父结点，满足B树条件，插入操作结束。

当阶数m为偶数时，需要分裂时就不存在排序恰好在中间的key，那么我们选择中间位置的前一个key或中间位置的后一个key为中心进行分裂即可。

---

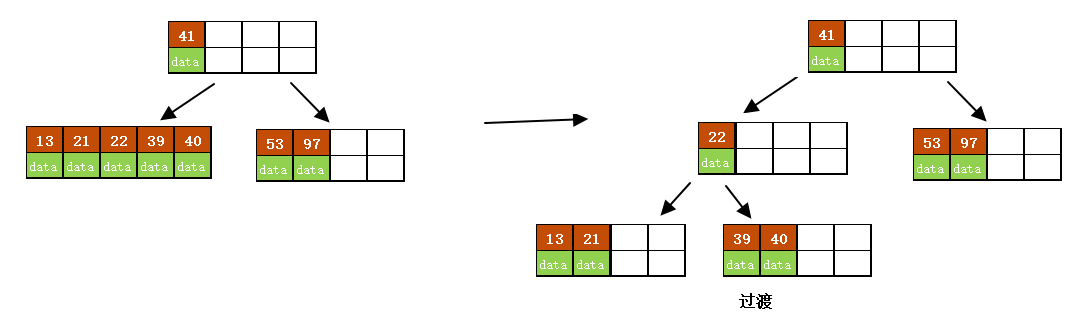
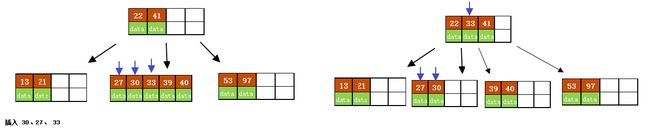
d）依次插入13、21、40，

同样会造成分裂，结果如下图所示。

---

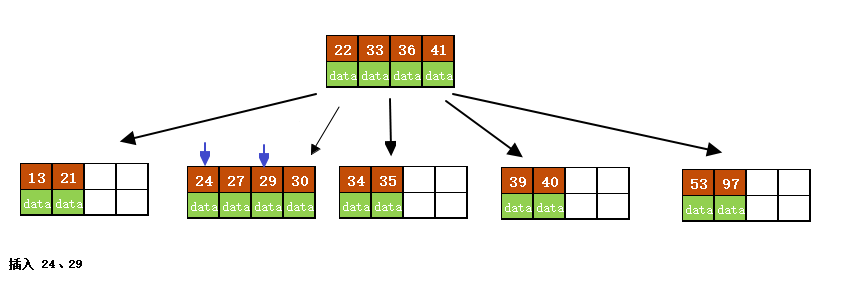
e）依次插入30、27、 33 ；36、35、34； 24、29，

插入 30、27、 33

---

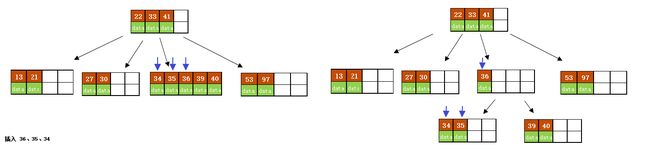
插入 36、35、34；

---

插入 24、29

结果如下图所示。

---

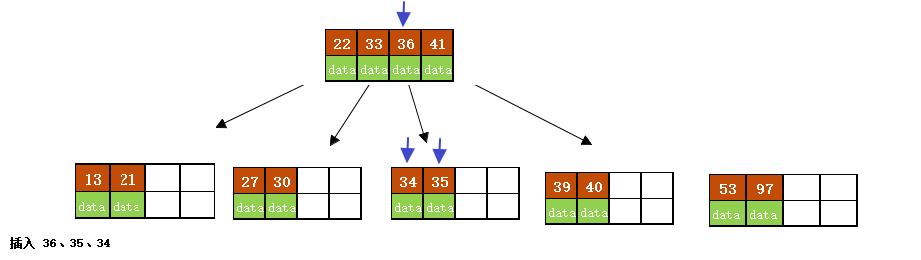
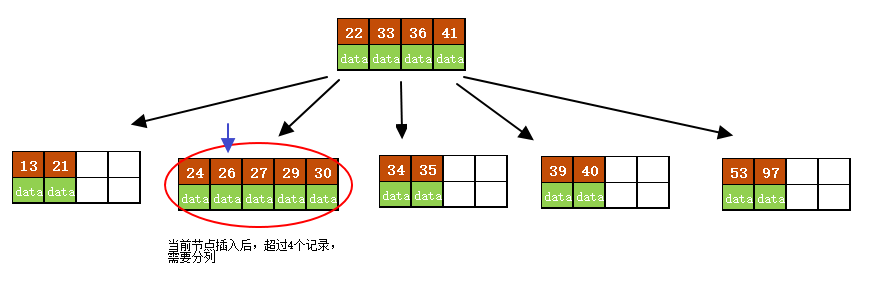
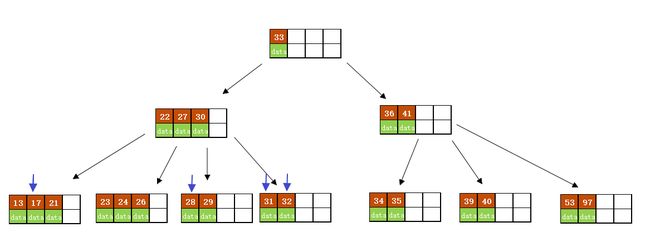
f）插入26

插入后的结果如下图所示。

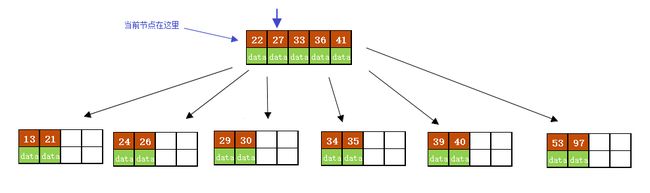
当前结点需要以27为中心分裂，并向父结点进位27，然后当前结点指向父结点，结果如下图所示。

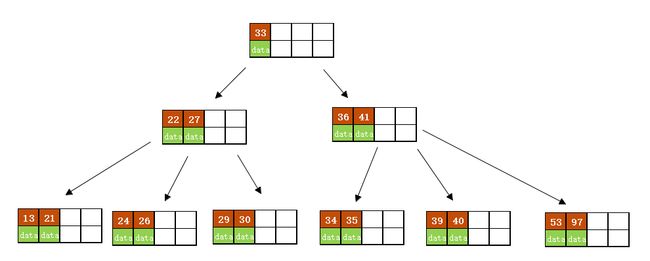
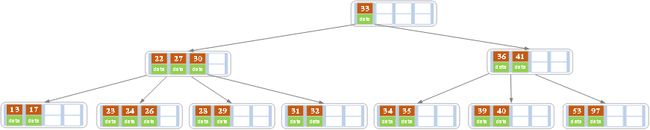
进位后导致当前结点（即根结点）也需要分裂，分裂的结果如下图所示。

分裂后当前结点指向新的根，此时无需调整。

---

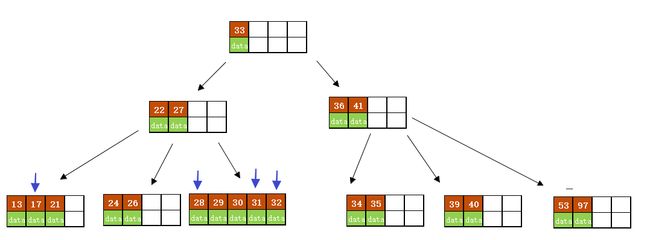
g）最后再依次插入key为 17、28、31、32 的记录，

结果如下图所示：

---

在实现B树的代码中，为了使代码编写更加容易，我们可以将结点中存储记录的数组长度定义为m而非m-1，这样方便底层的结点由于分裂向上层插入一个记录时，上层有多余的位置存储这个记录。同时，每个结点还可以存储它的父结点的引用，这样就不必编写递归程序。

一般来说，对于确定的m和确定类型的记录，结点大小是固定的，无论它实际存储了多少个记录。但是分配固定结点大小的方法会存在浪费的情况，比如key为28,29所在的结点，还有2个key的位置没有使用，但是已经不可能继续在插入任何值了，因为这个结点的前序key是27,后继key是30,所有整数值都用完了。所以如果记录先按key的大小排好序，再插入到B树中，结点的使用率就会很低，最差情况下使用率仅为50%。

3、 B树的删除操作

删除操作是指，根据key删除记录，如果B树中的记录中不存对应key的记录，则删除失败。

1）如果当前需要删除的key位于非叶子结点上，则用后继key（这里的后继key均指后继记录的意思）覆盖要删除的key，然后在后继key所在的子支中删除该后继key。此时后继key一定位于叶子结点上，这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步

2）该结点key个数大于等于Math.ceil(m/2)-1，结束删除操作，否则执行第3步。

3）如果兄弟结点key个数大于Math.ceil(m/2)-1，则父结点中的key下移到该结点，兄弟结点中的一个key上移，删除操作结束。

否则，将父结点中的key下移与当前结点及它的兄弟结点中的key合并，形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针，指向这个新结点。然后当前结点的指针指向父结点，重复上第2步。

有些结点它可能即有左兄弟，又有右兄弟，那么我们任意选择一个兄弟结点进行操作即可。

下面以5阶B树为例，介绍B树的删除操作

5阶B树中，结点最多有4个key,最少有2个key

a）原始状态

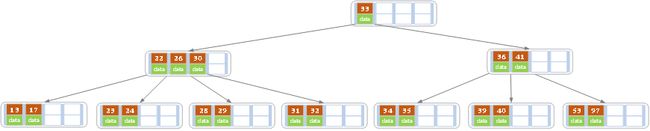
b）在上面的B树中删除21，删除后结点中的关键字个数仍然大于等2，所以删除结束。

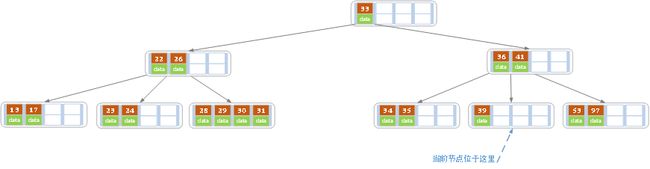
c）在上述情况下接着删除27。从上图可知27位于非叶子结点中，所以用27的后继替换它。从图中可以看出，27的后继为28，我们用28替换27，然后在28（原27）的右孩子结点中删除28。删除后的结果如下图所示。

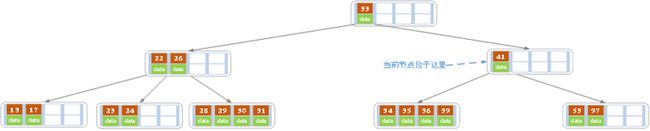
删除后发现，当前叶子结点的记录的个数小于2，而它的兄弟结点中有3个记录（当前结点还有一个右兄弟，选择右兄弟就会出现合并结点的情况，不论选哪一个都行，只是最后B树的形态会不一样而已），我们可以从兄弟结点中借取一个key。所以父结点中的28下移，兄弟结点中的26上移,删除结束。结果如下图所示。

d）在上述情况下接着32，结果如下图。

当删除后，当前结点中只key，而兄弟结点中也仅有2个key。所以只能让父结点中的30下移和这个两个孩子结点中的key合并，成为一个新的结点，当前结点的指针指向父结点。结果如下图所示。

当前结点key的个数满足条件，故删除结束。

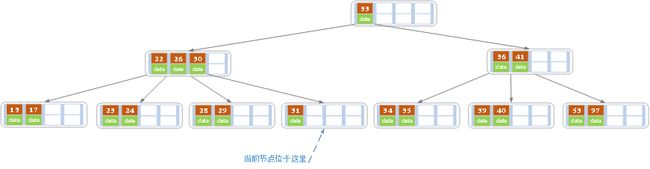
e）上述情况下，我们接着删除key为40的记录，删除后结果如下图所示。

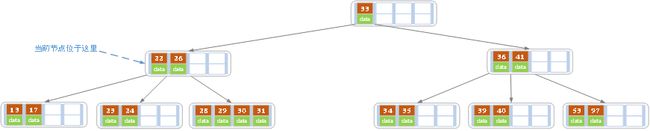
同理，当前结点的记录数小于2，兄弟结点中没有多余key，所以父结点中的key下移，和兄弟（这里我们选择左兄弟，选择右兄弟也可以）结点合并，合并后的指向当前结点的指针就指向了父结点。

同理，对于当前结点而言只能继续合并了，最后结果如下所示。

合并后结点当前结点满足条件，删除结束。

B树相关的文章

https://www.cnblogs.com/jing99/p/11736003.html

https://blog.csdn.net/kalikrick/article/details/27980007

https://blog.csdn.net/herry816/article/details/89525077

https://blog.csdn.net/jimo_lonely/article/details/82716142