丑数
第三十二题:丑数
题目描述
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
思路1:
暴力解:
从0开始,一直查找到第N个丑数为止,这里写一个判断该数字是否为丑数的方法,该方法的具体实现为:
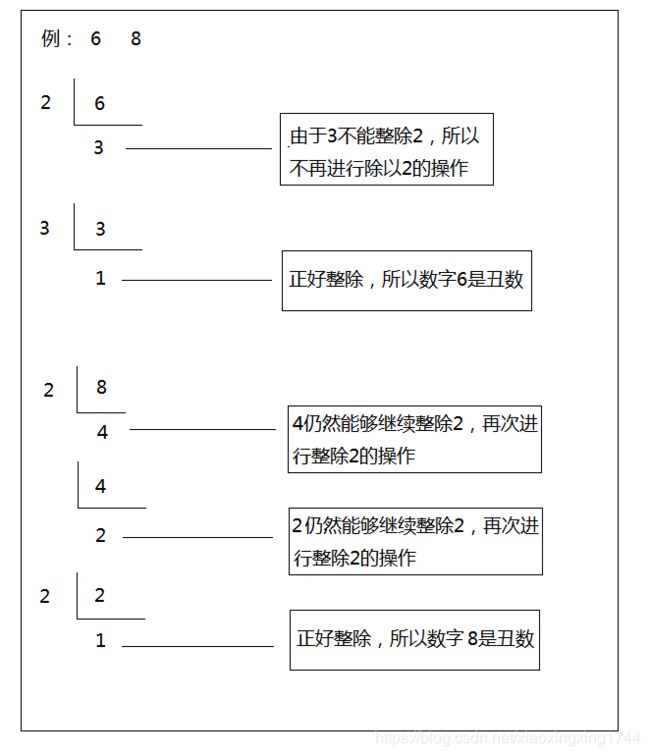
target一直除以2,3,5直到不能整除为止,如果余数为1,说明该数字为丑数。通过此方法找到第N个丑数
具体实现如下图所示:
具体实现代码如下:
public int GetUglyNumber_Solution(int index) {
// 代码的鲁棒性
if(index <= 0){
return 0;
}
// 累计丑数的数量
int uglyCount = 0;
int number = 1;
while (uglyCount < index){
if (isUgly(number)){
uglyCount++;
}
number++;
}
return number;
}
// 判断数字是否为丑数
public boolean isUgly(int number){
while (number % 2 == 0){
number /= 2;
}
while (number % 3 == 0){
number /= 3;
}
while (number % 5 == 0){
number /= 5;
}
return number == 1 ? true : false;
}思路2:
优化解:
说明:这里为引用牛客网牛友 事无巨细,悉究本末 的详细解释
首先从丑数的定义我们知道,一个丑数的因子只有2,3,5,那么丑数p = 2 ^ x * 3 ^ y * 5 ^ z,换句话说一个丑数一定由另一个丑数乘以2或者乘以3或者乘以5得到,那么我们从1开始乘以2,3,5,就得到2,3,5三个丑数,在从这三个丑数出发乘以2,3,5就得到4,6,10,6,9,15,10,15,25九个丑数,我们发现这种方法会得到重复的丑数,而且我们题目要求第N个丑数,这样的方法得到的丑数也是无序的。那么我们可以维护三个队列:
(1)丑数数组: 1
乘以2的队列:2
乘以3的队列:3
乘以5的队列:5
选择三个队列头最小的数2加入丑数数组,同时将该最小的数乘以2,3,5放入三个队列;
(2)丑数数组:1,2
乘以2的队列:4
乘以3的队列:3,6
乘以5的队列:5,10
选择三个队列头最小的数3加入丑数数组,同时将该最小的数乘以2,3,5放入三个队列;
(3)丑数数组:1,2,3
乘以2的队列:4,6
乘以3的队列:6,9
乘以5的队列:5,10,15
选择三个队列头里最小的数4加入丑数数组,同时将该最小的数乘以2,3,5放入三个队列;
(4)丑数数组:1,2,3,4
乘以2的队列:6,8
乘以3的队列:6,9,12
乘以5的队列:5,10,15,20
选择三个队列头里最小的数5加入丑数数组,同时将该最小的数乘以2,3,5放入三个队列;
(5)丑数数组:1,2,3,4,5
乘以2的队列:6,8,10,
乘以3的队列:6,9,12,15
乘以5的队列:10,15,20,25
选择三个队列头里最小的数6加入丑数数组,但我们发现,有两个队列头都为6,所以我们弹出两个队列头,同时将12,18,30放入三个队列;
……………………
疑问:
1.为什么分三个队列?
丑数数组里的数一定是有序的,因为我们是从丑数数组里的数乘以2,3,5选出的最小数,一定比以前未乘以2,3,5大,同时对于三个队列内部,按先后顺序乘以2,3,5分别放入,所以同一个队列内部也是有序的;
2.为什么比较三个队列头部最小的数放入丑数数组?
因为三个队列是有序的,所以取出三个头中最小的,等同于找到了三个队列所有数中最小的。
实现思路:
我们没有必要维护三个队列,只需要记录三个指针显示到达哪一步;“|”表示指针,arr表示丑数数组;
(1)1
|2
|3
|5
目前指针指向0,0,0,队列头arr[0] * 2 = 2, arr[0] * 3 = 3, arr[0] * 5 = 5
(2)1 2
2 |4
|3 6
|5 10
目前指针指向1,0,0,队列头arr[1] * 2 = 4, arr[0] * 3 = 3, arr[0] * 5 = 5
(3)1 2 3
2| 4 6
3 |6 9
|5 10 15
目前指针指向1,1,0,队列头arr[1] * 2 = 4, arr[1] * 3 = 6, arr[0] * 5 = 5
………………
总结:这样解的目的就是为了找到2和3和5倍数的最小值(从小到大的顺序)
具体实现如下图所示:
具体实现代码如下:
public int GetUglyNumber_Solution(int index) {
// 代码的鲁棒性
if(index <= 0){
return 0;
}
// 定义三个队列的指针
int temp2 = 0;
int temp3 = 0;
int temp5 = 0;
// 定义丑数数组
int[] arr = new int[index];
arr[0] = 1;
// next指针表示丑数数组中将要添加的丑数的位置
int next = 1;
while (next < index){
// 三个队列头部的最小值,并添加到丑数数组
int min = Math.min(Math.min(arr[temp2]*2, arr[temp3]*3), arr[temp5]*5);
arr[next++] = min;
// 最小值队列头部进行位移操作
while(arr[temp2]*2 <= min) {
temp2++;
}
while(arr[temp3]*3 <= min){
temp3++;
}
while(arr[temp5]*5 <= min){
temp5++;
}
}
return arr[index-1];
}