粒子群算法
粒子群优化(Particle Swarm Optimization, PSO),又称微粒群算法,是由J. Kennedy和R. C. Eberhart等于1995年开发的一种演化计算技术,来源于对一个简化社会模型的模拟。其中“群(swarm)”来源于微粒群符合M. M. Millonas在开发应用于人工生命(artificial life)的模型时所提出的群体智能的5个基本原则。“粒子(particle)”是一个折衷的选择,因为既需要将群体中的成员描述为没有质量、没有体积的,同时也需要描述它的速度和加速状态。
PSO算法最初是为了图形化的模拟鸟群优美而不可预测的运动。而通过对动物社会行为的观察,发现在群体中对信息的社会共享提供一个演化的优势,并以此作为开发算法的基础。通过加入近邻的速度匹配、并考虑了多维搜索和根据距离的加速,形成了PSO的最初版本。之后引入了惯性权重w来更好的控制开发(exploitation)和探索(exploration),形成了标准版本。为了提高粒群算法的性能和实用性,中山大学、(英国)格拉斯哥大学等又开发了自适应版本(Adaptive PSO).[1]
目录
[隐藏]- 1 算法原理
- 2 算法参数
- 2.1 收敛性
- 3 外部链接
- 4 参考文献
算法原理[编辑]
PSO算法是基于群体的,根据对环境的适应度将群体中的个体移动到好的区域。然而它不对个体使用演化算子,而是将每个个体看作是D维搜索空间中的一个没有体积的微粒(点),在搜索空间中以一定的速度飞行,这个速度根据它本身的飞行经验和同伴的飞行经验来动态调整。第i个微粒表示为Xi = (xi1, xi2, …, xiD),它经历过的最好位置(有最好的适应值)记为Pi = (pi1, pi2, …, piD),也称为pbest。在群体所有微粒经历过的最好位置的索引号用符号g表示,即Pg,也称为gbest。微粒i的速度用Vi = (vi1, vi2, …, viD)表示。对每一代,它的第d维(1 ≤ d ≤ D)根据如下方程进行变化:
vid = w∙vid+c1∙rand()∙(pid-xid)+c2∙Rand()∙(pgd-xid) (1a)
xid = xid+vid (1b)
其中w为惯性权重(inertia weight),c1和c2为加速常数(acceleration constants),rand()和Rand()为两个在[0,1]范围里变化的随机值。
此外,微粒的速度Vi被一个最大速度Vmax所限制。如果当前对微粒的加速导致它的在某维的速度vid超过该维的最大速度vmax,d,则该维的速度被限制为该维最大速度vmax,d。
对公式(1a),第一部分为微粒先前行为的惯性,第二部分为“认知(cognition)”部分,表示微粒本身的思考;第三部分为“社会(social)”部分,表示微粒间的信息共享与相互合作。
“认知”部分可以由Thorndike的效应法则(law of effect)所解释,即一个得到加强的随机行为在将来更有可能出现。这里的行为即“认知”,并假设获得正确的知识是得到加强的,这样的一个模型假定微粒被激励着去减小误差。
“社会”部分可以由Bandura的替代强化(vicarious reinforcement)所解释。根据该理论的预期,当观察者观察到一个模型在加强某一行为时,将增加它实行该行为的几率。即微粒本身的认知将被其它微粒所模仿。
PSO算法使用如下心理学假设:在寻求一致的认知过程中,个体往往记住自身的信念,并同时考虑同事们的信念。当其察觉同事的信念较好的时候,将进行适应性地调整。
标准PSO的算法流程如下:
- 初始化一群微粒(群体规模为m),包括随机的位置和速度;
- 评价每个微粒的适应度;
- 对每个微粒,将它的适应值和它经历过的最好位置pbest的作比较,如果较好,则将其作为当前的最好位置pbest;
- 对每个微粒,将它的适应值和全局所经历最好位置gbest的作比较,如果较好,则重新设置gbest的索引号;
- 根据方程(1)变化微粒的速度和位置;
- 如未达到结束条件(通常为足够好的适应值或达到一个预设最大代数Gmax),回到2)。
算法参数[编辑]
PSO参数包括:群体规模m,惯性权重w,加速常数c1和c2,最大速度Vmax,最大代数Gmax。
Vmax决定在当前位置与最好位置之间的区域的分辨率(或精度)。如果Vmax太高,微粒可能会飞过好解,如果Vmax太小,微粒不能进行足够的探索,导致陷入局部优值。该限制有三个目的:防止计算溢出;实现人工学习和态度转变;决定问题空间搜索的粒度。
惯性权重w使微粒保持运动的惯性,使其有扩展搜索空间的趋势,有能力探索新的区域。
加速常数c1和c2代表将每个微粒推向pbest和gbest位置的统计加速项的权重。低的值允许微粒在被拉回来之前可以在目标区域外徘徊,而高的值导致微粒突然的冲向或者越过目标区域。
如果没有后两部分,即c1 = c2 = 0,微粒将一直以当前的速度飞行,直到到达边界。由于它只能搜索有限的区域,将很难找到好的解。
如果没有第一部分,即w = 0,则速度只取决于微粒当前的位置和它们历史最好位置pbest和gbest,速度本身没有记忆性。假设一个微粒位于全局最好位置,它将保持静止。而其它微粒则飞向它本身最好位置pbest和全局最好位置gbest的加权中心。在这种条件下,微粒群将统计的收缩到当前的全局最好位置,更象一个局部算法。
在加上第一部分后,微粒有扩展搜索空间的趋势,即第一部分有全局搜索的能力。这也使得w的作用为针对不同的搜索问题,调整算法全局和局部搜索能力的平衡。
如果没有第二部分,即c1 = 0,则微粒没有认知能力,也就是“只有社会(social-only)”的模型。在微粒的相互作用下,有能力到达新的搜索空间。它的收敛速度比标准版本更快,但是对复杂问题,比标准版本更容易陷入局部优值点。
如果没有第三部分,即c2 = 0,则微粒之间没有社会信息共享,也就是“只有认知(cognition-only)”的模型。因为个体间没有交互,一个规模为m的群体等价于m个单个微粒的运行。因而得到解的几率非常小。
收敛性[编辑]
收敛性的数学证明帮助了PSO的发展和应用[2], 但此内分析具有很大的局限性.[3] 为PSO加入正交学习后,算法的全局收敛、收敛精度及鲁棒可靠性都得到了提高.[4]
上次在自话遗传算法中提到后期会写两篇关于粒子群算法和蚁群算法的博文,所以这次给大家带来的是我对粒子群的一些理解,并附带一个相当简单的实例去描述这个算法,我会尽力通俗易懂的把整个算法描述一遍,其实粒子群算法的思想也挺简单的,希望我不要反而写复杂了,下面同样引用百度百科的摘要结束简介部分。
粒子群优化算法(PSO)是一种进化计算技术(evolutionary computation),1995 年由Eberhart 博士和kennedy 博士提出,源于对鸟群捕食的行为研究 。该算法最初是受到飞鸟集群活动的规律性启发,进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上,利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得最优解。
基本思想
正如简介所描述的那样,粒子群算法是模拟群体智能所建立起来的一种优化算法,像后面我向大家介绍的蚁群算法也属于这类算法,粒子群算法可以用鸟类在一个空间内随机觅食为例,所有的鸟都不知道食物具体在哪里,但是他们知道大概距离多远,最简单有效的方法就是搜寻目前离食物最近的鸟的周围区域。
所以,粒子群算法就是把鸟看成一个个粒子,并且他们拥有位置和速度这两个属性,然后根据自身已经找到的离食物最近的解和参考整个共享于整个集群中找到的最近的解去改变自己的飞行方向,最后我们会发现,整个集群大致向同一个地方聚集。而这个地方是离食物最近的区域,条件好的话就会找到食物。这就是粒子群算法,很好理解。
算法描述
所以,我们需要一个pbest来记录个体搜索到的最优解,用gbest来记录整个群体在一次迭代中搜索到的最优解。速度和粒子位置的更新公式如下:
v[i] = w * v[i] + c1 * rand() * (pbest[i] - present[i]) + c2 * rand() * (gbest - present[i])
present[i] = present[i] + v[i]
其中v[i]代表第i个粒子的速度,w代表惯性权值,c1和c2表示学习参数,rand()表示在0-1之间的随机数,pbest[i]代表第i个粒子搜索到的最优值,gbest代表整个集群搜索到的最优值,present[i]代表第i个粒子的当前位置。
我这里打了一个求解y=-x*(x-1) 在[-2,2]上最大值的粒子群算法,选用这个简单的例子主要是能让大家清楚的看到效果和粒子的运动方向,也方便理解我想说的一些观点。代码如下:
输出结果如下:
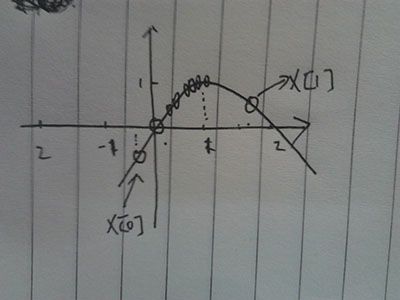
我们可以从打印的数据看出来,刚开始x[0]和x[1]分散在最大值两边,然后x[0]和x[1]逐渐聚集到1的周围,这里,我们已经收敛到x=1这个地方了,这正是我们要求的最大值,其最大值为1,下面是图解过程。
1.初始状态
2.第二次x[1]向左边移动了
3.最后,两点聚集在1上,上面多个圈是他们聚集的过程,可以看出来,聚集过程是个越来越密集的过程。
最后
粒子群算法,相对于我上次提到的遗传算法而言编码要简单很多,同样属于进化算法,但是粒子群算法并没有像遗传算法那样有选择交叉变异这样的过程,而更多的是体现在追踪单个粒子和共享集体最优信息来实现向最优空间搜索的形式,但是正由于它不同于遗传算法那样去忽略个体的一些内在联系,所以往往会陷入局部最优,所以,在粒子群算法中加入像遗传算法中的变异或者模拟退火等,可以跳过这个局部最优解。
而惯性权值对于函数收敛速度和是否收敛有很大的决定作用,两个学习参数c1,c2的制定也同等重要,但是即使这样,它也没有遗传算法中会有多个参数去维护,所以整个算法就那一个公式就行了,相当的清晰。在遗传算法中的信息的共享是染色体互相之间通过交叉共享,所以在搜索移动过程显得平均缓慢,而粒子群算法是根据gbest来决定整个集群的单向移动,所以相对遗传算法,它更快的收敛。
这不由得让我想到了熵这个概念,在诸如我们社会甚至宇宙这样复杂的系统,我们都处于一个无序的状态,属于熵增状态,像粒子群,遗传算法,对群体的研究,体现的智能不就是在这个无序的系统提供有序的能量,然后它就逐渐有序了。对于智能,我想我有更深的体会了。这段话属于发神经,不作参考。