图算法系列之最短路算法Dijkstra(Java)
引言
假如你有一张地图,地图上给出了每一对相邻城市的距离,从一个地点到另外一个地点,如何找到一条最短的路? 最短路算法要解决的就是这类问题。今年的华为精英挑战赛codeCraft中关于部署大数据下网络服务器部署问题就需要使用最短路算法,因为求最小流最大费用算法时, 最核心的就是找出最短路,可见最短路算法的应用之广泛。
一.定义:
给定一个有(无)向图,每一条边有一个权值 w,给定一个起始点 S 和终止点 T ,求从 S 出发走到 T 的权值最小路径,即为最短路径。最短路算法依赖一种性质:一条两顶点间的最短路径包含路径上其他最短路径。简单的说就是:最短路径的子路径是最短路径。
二.最短路算法
最常用的最短路算法是Dijkstra算法、A*算法、SPFA算法、Bellman-Ford算法和Floyd-Warshall算法,我们这里重点介绍并实现Dijkstra和SPFA,以及A*算法,其他算法只介绍原理,不展开
1.松弛技术(Relaxation)(非常重要)
松弛操作的原理是著名的定理:“三角形两边之和大于第三边”,在信息学中我们叫它三角不等式。所谓对结点i,j进行松弛,就是判定是否dis[j]>dis[i]+w[i,j],如果该式成立则将dis[j]减小到dis[i]+w[i,j],否则不动。
2.Dijkstra算法
解决最短路问题,最经典的算法是 Dijkstra算法,它是一种单源最短路算法,其核心思想是贪心算法(Greedy Algorithm),Dijkstra算法由荷兰计算机科学家Dijkstra发现,这个算法至今差不多已有50年历史,但是因为它的稳定性和通俗性,到现在依然强健。另外,Dijkstra算法要求所有边的权值非负。
1) Dijkstra算法思想为:
设 G = (V, E) 是一个带权有向图,把图中顶点集合 V 分成两组,第一组为已求出最短路径的顶点集合(用 S 表示,初始时 S 中只有一个源点,以后每求得一条最短路径 , 就将其加入到集合 S 中,直到全部顶点都加入到 S 中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用 U 表示),按最短路径长度的递增次序依次把第二组的顶点加入 S 中。在加入的过程中,总保持从源点 v 到 S 中各顶点的最短路径长度不大于从源点 v 到 U 中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S 中的顶点的距离就是从 v 到此顶点的最短路径长度,U 中的顶点的距离,是从 v 到此顶点只包括 S 中的顶点为中间顶点的当前最短路径长度。
2)算法核心步骤如下:
a. 将所有顶点分为两部分:已知最短路程的顶点集合P和未知最短路径的顶点集合Q。最开始,已知最短路径的顶点集合P中只有源点一个顶点。我们这里用一个isVisited数组来记录哪些顶点再集合P中。例如对于某个顶点i,如果isVisited[i]为1则表示这个顶点再集合P中,如果isVisited[i]为0则表示这个顶点再集合Q中。
b. 设置源点s到自己的最短路径为0即 dis[s]=0。若存在有源点能直接到达的顶点i,则把dis[i]设为w[s][i]。同时把所有其他(源点不能直接到达的)顶点的最短路径设为∞。
c. 在集合Q的所有顶点中选择一个离源点s最近的顶点u(即dis[u]最小)加入到集合P。并考察所有以点u为起点的边,对每一条边进行松弛操作。例如存在一条从u到v的边,那么可以通过将u->v添加到尾部来拓展一条从s到v的路径,这条路径的长度时dis[u]+w[u][v]。如果这个值比目前已知的dis[v]的值要小,我们可以用新值来替代当前dis[v]中的值。
d. 重复第3步,如果集合Q为空,算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。
补充:dis数组用来记录起点到所有顶点的距离,Path[]数组,Path[i]表示从S到i的最短路径中,结点i之前的结点的编号。注意,是“之前”,不是“之后”。最短路径算法的核心思想成为“松弛”,原理是三角形不等式,我们只需要在借助结点u对结点v进行松弛的同时,标记下Path[v] = u,记录的工作就完成了。
3)算法案例图解
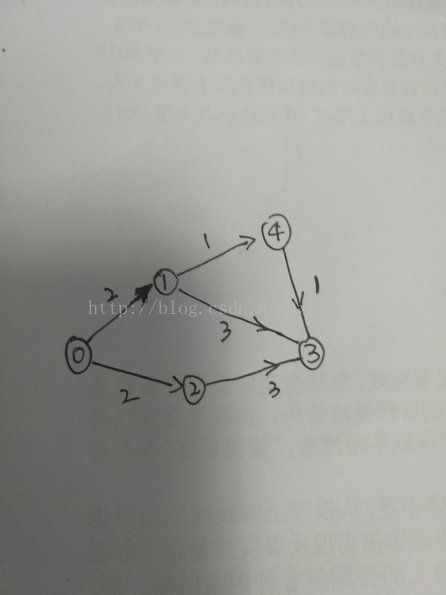
计算从源顶点1到其它顶点间的最短路径,对下图中的有向图,应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下面的表中。
Dijkstra算法的迭代过程:
三.最短路算法Java实现
1.顶点结构
public class Vertex {
//存放点信息
public int data;
//与该点邻接的第一个边节点
public Edge firstEdge;
} 2.边结构
//边节点
public class Edge {
//对应的点下表
public int vertexId;
//边的权重
public int weight;
//下一个边节点
public Edge next;
//getter and setter自行补充
} import java.util.*;
public class graph {
public Vertex[] vertexList; //存放点的集合
public graph(int vertexNum){
this.vertexNum=vertexNum;
vertexList=new Vertex[vertexNum];
}
//点个数
public int vertexNum;
//边个数
public int edgeLength;
public void initVertext(){
for(int i=0;i4.Dijkstra算法
package MSP;
import java.util.*;
public class Dijkstra {
public graph gh;
public Dijkstra(graph gh){
this.gh=gh;
}
//未求出最短路径的点集合
public ArrayList unVisited=new ArrayList();
//已求出最短路径的点集合
public ArrayList hasVisited=new ArrayList();
//记录从起点到其他任意一点的路径长度
public int distances[];
//记录Path[i]表示从S到i的最短路径中,结点i之前的结点的编号,即对应点的前一个节点
public int paths[];
/**
* 初始化各点距离及路径
*/
public void init(int x,int y ){
distances=new int[gh.vertexNum];
paths=new int[gh.vertexNum];
for(int i=0;i"+i+"距离为"+distances[i]);
}
ArrayList mypath=printPath(x,y);
StringBuilder sb=new StringBuilder();
sb.append("路径为:");
for(int i=0;i");
}
sb.delete(sb.length()-3,sb.length());
System.out.println(sb.toString());
}
/**
* 求出从x到y的路径,由于path中存放的该点的前一个点的位置
* @param x
* @param y
*/
public ArrayList printPath(int x,int y){
ArrayList mypaths=new ArrayList();
while(y!=x){
mypaths.add(y);
y=paths[y];
}
mypaths.add(x);
//路径倒置,需要反置回来
Collections.reverse(mypaths);
return mypaths;
}
/**
* 考察所有以点u为起点的边,对每一条边进行松弛操作。
* @param u
*/
public void relax(int u){
for(Edge edge=gh.vertexList[u].firstEdge;edge!=null;edge=edge.next){
int v=edge.vertexId;
//对v进行松弛,看是否满足distances[v]>distances[u]+w[u][v]
int w=edge.weight;
if(distances[v]>distances[u]+w){
distances[v]=distances[u]+w;
//记录v的最短路径时,前一个节点为u
paths[v]=u;
}
}
}
/**
* 从未求出最短路径的集合中找到与原点最近的点
* @param x
*/
public int pickMinInUnvisited(int x){
int minIndex=-1;
int min=Integer.MAX_VALUE;
for(int i=0;i 执行结果如下:
1-->0距离为2147483647
1-->1距离为0
1-->2距离为2147483647
1-->3距离为2
1-->4距离为1
路径为:1-->4-->3