文本分类——常见分类模型
内容提要
- 基于规则的模型
- 基于概率的模型
- 基于几何的模型
- 基于统计的模型
文本分类方法模型主要分为两个大类,一类是基于规则的分类模型;另一类是基于概率统计的模型。
基于规则的模型
基于规则的分类模型相对简单,易于实现。它在特定领域的分类往往能够取得较好的效果。相对于其它分类模型来说,基于规则的分类模型的优点就是时间复杂度低、运算速度快。在基于规则的分类模型中,使用许多条规则来表述类别。类别规则可以通过领域专家定义,也可以通过计算机学习获得。
决策树就是一种基于训练学习方法获取分类规则的常见分类模型,它建立对象属性与对象值之间的一种映射。通过构造决策树来对未标注文本进行分类判别。常用的决策树方法包括CART 算法、ID3、C4.5、CHAID 等。
在Web文本应用领域普遍存在着层级形式,这种层级形式可以通过一颗决策树来描述。决策树的根节点表示整个数据集空间,每个子节点是依据单一属性做出的分支判定,该判定将数据集分成两个或两个以上的分支区域。决策树的叶子节点就是相应类别的数据集合。
决策树分类模型的一般构建过程:
1.首先将训练数据分成两部分,一部分(训练集A)用于构建初始决策树,另一部分(训练集B)用来对决策树进行剪枝;
2.以训练集A作为树的根节点,找出变异量最大的属性变量作为高层分割标准;以训练集A作为树的根节点,找出变异量最大的属性变量作为高层分割标准;
3.通过对训练集A的学习训练构建一颗初始决策树;通过对训练集A的学习训练构建一颗初始决策树;
4.再通过训练集B对初始决策树进行剪枝操作;再通过训练集B对初始决策树进行剪枝操作;
5.一般还要通过递归的过程来构建一颗稳定的决策树,根据预测结果的正确率及未满足条件,则再对决策树进行分支或剪枝。
决策树的构建过程一般是自上而下的,剪枝的方法有多种,但是具有一致目标,即对目标文本集进行最优分割。决策树可以是二叉树也可以是多叉树。
基于概率的模型
假设未标注文档为d,类别集合为C={c1,c2,…,cm} ,概率模型分类是对1≤i≤n 求条件概率模型P(ci|d) ,将与文档d条件概率最大的那个类别作为该文档的输出类别。其中朴素贝叶斯分类器是应用最为广泛的概率分类模型。
朴素贝叶斯分类的基本思想是利用词组与类别的联合概率来估计给定文档的类别概率。基于贝叶斯分类器的贝叶斯规则如式:

其中:C和D为随机变量。
贝叶斯规则计算文档d属于每一个类别的可能性 P(ci|d),然后将文档d标注为概率最大的那一类。对文档d的贝叶斯分类如下式

先验概率P(ci) 的估计很简单,计算如下式所示:

其中: N(ci) 表示训练集中类别ci 的样本数量,N为训练集样本总数。 本质上表示训练集样例中类别ci 的比例。
概率P(d|ci) 计算相对复杂,它首先基于一个贝叶斯假设:文档d为词组元素的集合,集合中词组(元素)之间相互独立。由于文档的表示简化了,所以这也就是朴素(Naïve) 的由来之一。事实上,词组之间并不是相互独立的。虽然这是一种假设独立性,但是朴素贝叶斯还是能够在分类任务中表现出很好的分类效果和鲁棒性。这一假设简化了联合概率的计算,它允许条件概率的乘机来表示联合概率。P(d|ci) 的计算式:
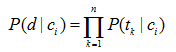
其中:tk 表示含有n项词组的词组表vi 中的一个词组。因此,估计P(d|ci) 变为估计词组表v中的每一个词组在每一个类别下的概率P(tk|ci) 。
概率的估计与分类结果非常依赖于事件空间的选择。下面介绍两种卡内基梅隆大学McCallum 和 Nigam 提出的事件空间模型,并说明相应的P(tk|ci) 是如何估计的。
1) 多重伯努利模型
多重伯努利(Multiple-Bernoulli)事件空间是一种布尔独立模型的事件空间,为每一个词组tk 建立一个二值随机变量。最简单的方式就是使用最大似然估计来估计概率,即式:

其中: df(tk|ci) 表示类别ci 含有词组tk 的样本数量。
虽然上式来估计概率很简单,但是存在“零概率”问题,真实应用是不可能的。这就需要采用平滑技术来克服“零概率”问题。贝叶斯平滑是一种常用的平滑估计技术。多重伯努利模型的平滑估计如下式所示:
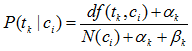
其中: αk 与βk 是依赖与词组tk 的参数。一种常见的参数选择方式是αk =1且βk* =0,得到如下概率估计公式

多重伯努利模型仅仅考虑词组是否出现,而没有考虑出现的多少,而词频也是一个重要分类信息。下面介绍加入词频信息的多项式模型。
2) 多项式模型
多项式(Multinomial)时间空间与多重伯努利事件空间类似,但是多项式事件空间假设词组的出现次数是零次或多次,而不是出现与否。
多项式模型的最大似然估计计算如式:

其中: tf(tk|ci) 表示训练集中类别ci 中词组tk 出现的次数。 |ci|表示训练集类别ci 中的总词数。加入平滑估计的概率如式:

这里 αk 是依赖于词组tk 的参数。对所有词组tk* 取αk =1是一种常见选择。这就导致概率估计:
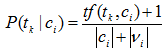
实际应用中,多项式模型已经表明优于多重伯努利模型。
基于几何的模型
使用向量空间模型表示文本,文本就被表示为一个多维的向量,那么它就是多维空间的一个点。通过几何学原理构建一个超平面将不属于同一个类别的文本区分开。最典型的基于几何学原理的分类器是支持向量机(SVM),最简单的SVM应用就是二值分类,就是常见的正例和反例。SVM的目标就是构建能够区分正例和反例的N维空间决策超平面。
SVM是上世纪九十年代中期,由Vapnik等人逐渐完善的统计机器学习理论。该模型主要用来解决模式识别中的二分类问题,在文本分类、手写识别、图像处理等领域都取得了很好的分类效果。其基本思想就是在向量空间中找到一个决策超平面,该决策超平面能够最大限度地将正例和反例区分开来。在一定的范围内,决策超平面是可以平行移动的,这种平移不会造成训练集数据的分类错误。但是为了获取在未知样本的分类预测中的稳定性,要求分类超平面距离两类样本的距离尽可能大,也就是说,超平面尽可能位于边界区域的中心位置。
SVM采用计算学习理论的结构风险最小化(Structural Risk Minimization, SRM)原则。其主要思想:以支持向量(Support Vector, SV)作为训练集的基础,在N维空间内寻找能将训练集样本分成两类,并且具有最大边缘(Margin)值的最优超平面(Optimal Separating Hyper-plane,OSH),来达到最大的分类正确率。
SVM选择最大化边缘距离的分类决策超平面,这个选择不仅直观,而且也得到了理论的支持。对于线性可分数据的超平面以及支持向量的图形解释如图:
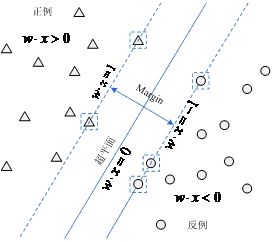
其中:左上方为正例区域,右下方为反例区域,中间实线为w定义的决策超平面,箭头所示为边缘,虚线方框内的样本表示支持向量。边缘(Margin)的定义如式:

其中:x- 是训练集距离超平面最近的反例, x+ 是训练集距离超平面最近的正例。定义边缘(Margin)为x- 到决策超平面距离与x+ 到决策超平面距离之和。
SVM算法中超平面的概念是发现使分离数据最大边缘化的超平面w。一个等价的形式是,寻找解决下列优化问题的决策超平面,如式:
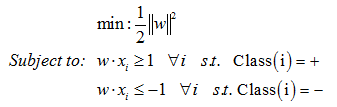
这一优化目标容易求解,一般通过动态规划来解决。
现实世界中的数据集很少是线性可分的。为了解决这个问题,一般需要修改SVM优化目标公式加入惩罚因子来完成不满足线性可分约束的训练实例的分类。加入了惩罚因子的SVM最优化目标如式:
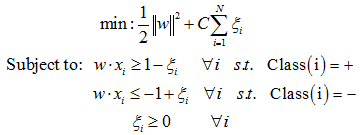
这里ζi 表示允许目标被违反的松弛变量(Stack Variable),这个松弛变量加强了关键损失函数。
另外一个SVM关键技术是核技巧,通过核函数将线性不可分的训练数据变换或映射到更高维空间中,得到线性可分的数据集。核函数技术大多数情形下都可以提高分类的精度。常用SVM核函数如下:
线性核:
多项式核:
径向基(RBF)核(也称为高斯核):
SVM能够取得比较好的分类效果。其优点在于:
1.SVM是一种针对有限样本条件下的分类算法,其目标是得到当前训练集下的最优解而不是样本数趋于无穷大时的最优值,该算法最终将问题转化成二次线性规划寻求最优解问题。从理论上来讲,它得到的是全局最优解,能够避免局部极值问题。
2.该方法将实际问题通过核函数技巧将线性不可分空间映射到高维线性可分空间,在高维空间中构造线性决策函数来实现原线性不可分空间的决策函数。这保证了SVM具有较好的推广能力,计算的复杂度不再取决于空间维数,而是取决于训练集样本数量。
3.SVM方法能够很好的处理稀疏数据,更好的捕捉了数据的内在特征,准确率较高。
SVM虽然有许多优点,但是固有的缺点是不可避免的。其缺点包括:
1.SVM算法时间和空间复杂度较高,随着训练样本数和类别的增加,分类时间和空间代价很高。
2.核函数空间变换会增加训练集空间的维数,使得SVM对时间和空间需求加大,又进一步降低了分类的效率。
3.SVM算法一般含有较多参数,并且参数随着训练样本的不同,呈现较大的差异,调整参数以获得最优分类效果相对困难。而且参数的不同对分类结果的显示出较大的差异性。
基于统计的模型
基于统计的机器学习方法已经成为自然语言研究领域里面的主流研究方法。事实上无论是朴素贝叶斯分类模型,还是支持向量机分类模型,也都采用了统计的方式。文本分类算法中一种最典型的基于统计的分类模型就是k近邻(k-Nearest Neighbor,kNN)模型,是比较好的文本分类算法之一。
kNN分类模型的主要思想:通过给定一个未标注文档d,分类系统在训练集中查找与它距离最接近的k篇相邻(相似或相同)标注文档,然后根据这k篇邻近文档的分类标注来确定文档d的类别。分类实现过程:
1) 将训练集样本转化为向量空间模型表示形式并计算每一特征的权重;
2) 采用类似步骤1的方式转化未标注文档d并计算相应词组元素的权重;
3) 计算文档d与训练集样本中每一样本的距离(或相似度);
4) 找出与文档d距离最小(或相似度最大)的k篇训练集文本;
5) 统计这个k篇训练集文本的类别属性,一般将文档d的类归为k中最多的样本类别。
kNN 分类模型是一种“懒学习”算法,实质上它没有具体的训练学习过程。分类过程只是将未标注文本与每一篇训练集样本进行相似度计算, kNN 算法的时间和空间复杂度较高。因而随着训练集样本的增加,分类的存储资源消耗大,时间代价高。一般不适合处理训练样本较大的分类应用。
| 知更鸟博文推荐 | |
|---|---|
| 上一篇 | 文本分类——特征选择概述 |
| 下一篇 | 文本分类——算法性能评估 |
| 推荐篇 | 基于Kubernetes、Docker的机器学习微服务系统设计——完整版 |
| 研究篇 | RS中文分词 | MP特征选择 | NLV文本分类 | 快速kNN |
| 作者简介 | |
| 兴趣爱好 | 机器学习、云计算、自然语言处理、文本分类、深度学习 |
| [email protected] (欢迎交流) | |
参考文献:
[1].McCallum,A.,Nigam,K. A comparison of event models for naive Bayes text classification [C]. In: Proc. of the AAAI ’98 Workshop on Learning for Text Categorization. 41 - 48.
[2].宗成庆. 统计自然语言处理[M].北京:清华大学出版社,2008
[3].王斌,潘文峰.基于内容的垃圾邮件过滤技术综述[J].中文信息学报,19(5):1-10
[4].Yang,Y.,Liu,X. A re-examination of text categorization methods [C]. In: Proceedings of the 22nd ACM Int’l Conference on Research and Development in Information Retrieval. Berkeley: ACM Press: 42-49