多进制LDPC码的译码算法比较

总结对比一下多进制LDPC的译码算法

一、多进制 BP、SPA译码算法 

 这个是最基本的译码算法，可以从二进制直接扩展引用过来。在译码过程中传递的信息是码字符号取不同值的概率值（二进制是0和1，多进制是0到q-1个概率值），符号的几个概率值的叠加的运算就是累乘，复杂度高，但是性能好。

二、多进制Log—BP、Log—SPA 

 跟二进制Log-BP略有不同，主要不同点如下： 

 1.初始化 二进制的Log—BP初始化时的公式是：2*y/sigma^2    多进制的Log-BP初始化时的公式是：2*s_y/sigma^2 

 %接收后处理
        f=reshape(zb,nbits,length(y));  % reshape for finding priors on symbols 将列向量重构成两行向量
        PP=zeros(q-1,n);
        for i=1:q-1
            a=dec2bin(i,nbits);
            for j=1:nbits
                if(a(j)=='1')
                PP(i,:)=PP(i,:)+f(j,:);
                end
            end
        end
        PP=2*PP/sigma^2;        % likelihoods for bits 这里说的是第n个符号去值为a（0~q-1）的概率

 2. 校验节点更新

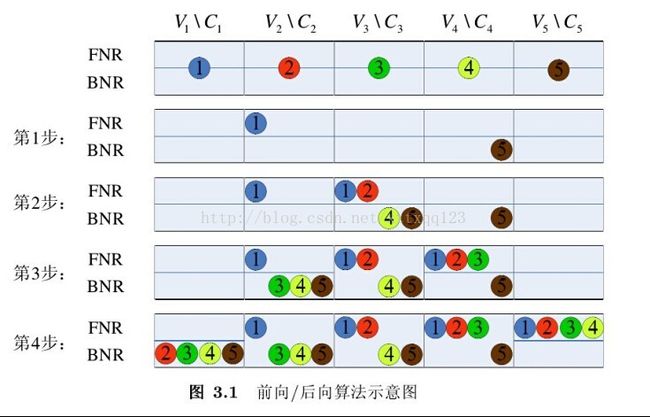
    多进制的校验节点更新采用的是前向-后向算法

如图，一个与5个变量节点相连的校验节点，进行的前向-后向运算，需要10个存储单元。前向-后向同时进行运算，每次运算结果跟下一个变量节点继续运算。如图第4步运算完后，再各个变量节点对应的上层（前向运算结果）和下层（后项运算结果）与本身节点进行运算。具体的前向-后向运算程序如下：

for i=1:m
     cl=find(H(i,:));
     a=length(cl);
     Fnr=zeros(q-1,a);
     Bnr=zeros(q-1,a);
     L=zeros(q-1,a);
     
     a1=H(i,cl(1));
     a1_E=power(beta(a1+1)+1); %这里是校验方程中第一个节点对应的Hmn
     for ii=1:q-1
         ii_E=power(beta(ii+1)+1);
         ij_E=gfmul(ii_E,a1_E,field);
         if ij_E == -Inf
             ij = 0;
         else
             ij = alpha(ij_E + 2);     % 十进制
         end
         Fnr(ij,2)=qij((q-1)*(i-1)+ii,cl(1)); %置换之后的qij赋值给前向运算第2项
     end
     
     aa=H(i,cl(a));
     aa_E=power(beta(aa+1)+1); %校验方程中的最后一个节点对应的Hmn
     for ii=1:q-1
         ii_E=power(beta(ii+1)+1);
         ij_E=gfmul(ii_E,aa_E,field);
         if ij_E == -Inf
             ij = 0;
         else
             ij = alpha(ij_E + 2);     % 十进制
         end
         Bnr(ij,a-1)=qij((q-1)*(i-1)+ii,cl(a)); %置换之后的qij赋值给后向运算倒数第2项
     end
     
     for j=3:a
         a2=H(i,cl(j-1));
         L2=qij(((q-1)*(i-1)+1):((q-1)*(i-1)+(q-1)),cl(j-1));
         a1=1;
         L1=Fnr(:,j-1);
         Fnr(:,j)=T_operate_max(a1,a2,L1,L2,q);
         
         a2=H(i,cl(a+2-j)); 
         L2=qij(((q-1)*(i-1)+1):((q-1)*(i-1)+(q-1)),cl(a+2-j));
         a1=1;
         L1=Bnr(:,a+2-j);
         Bnr(:,a+1-j)=T_operate_max(a1,a2,L1,L2,q);
     end
     
     a0=H(i,cl(1));
     a0_E=power(beta(a0+1)+1);
     for ii=1:q-1
         ii_E=power(beta(ii+1)+1);
         ij_E=gfdiv(ii_E,a0_E,field);
         if ij_E == -Inf
             ij = 0;
         else
             ij = alpha(ij_E + 2);     % 十进制
         end
         L(ij,1)=Bnr(ii,1);
         rij((q-1)*(i-1)+ij,cl(1))=L(ij,1);
     end
     
     aa=H(i,cl(a));
     aa_E=power(beta(aa+1)+1);
     for ii=1:q-1
         ii_E=power(beta(ii+1)+1);
         ij_E=gfdiv(ii_E,aa_E,field);
         if ij_E == -Inf
             ij = 0;
         else
             ij = alpha(ij_E + 2);     % 十进制
         end
         L(ij,a)=Fnr(ii,a);
         rij((q-1)*(i-1)+ij,cl(a))=L(ij,a);
     end    
     
     for j=2:a-1
         a0=H(i,cl(j));
         a0_E=power(beta(a0+1)+1);
         ii_E=power(beta(1+1)+1);
         ij_E=gfdiv(ii_E,a0_E,field);
         if ij_E == -Inf
             ij = 0;
         else
             ij = alpha(ij_E + 2);     % 十进制
         end
         a1=ij;
         a2=a1;
         L1=Fnr(:,j);
         L2=Bnr(:,j);
         L(:,j)=T_operate_max(a1,a2,L1,L2,q);
         rij(((q-1)*(i-1)+1):((q-1)*(i-1)+(q-1)),cl(j))=L(:,j);
     end
end

具体每一步的运算采用的是田字运算，田字运算程序如下：

 function [L]=T_operate_max(A1,A2,L1,L2,q)
 
%   clc
%   clear
%   L1=[0.5401 -3.7422 -3.3031];
%   L2=[2.8676  5.3361 -8.2037];
%   A1=2;
%   A2=3;
%   q=4;
  
   L=zeros(q-1,1);
   M=log2(q);   % 多进制 q 下取对数
   P=2;    
   field=gftuple((-1:P^M-2)',M, P);             % % % % M=log2(q); % GFq exponent
   [tuple power] = gftuple((-1:P^M-2)', M, P);  % tuple：域内元素的二进制向量表示(全0到全1间取值)  power：域内元素的本源元表示
   alpha = tuple * P.^(0 : M - 1)';             %  alpha：域内元素的十进制表示（0到2^M-1）
   beta(alpha + 1) = 0 : P^M - 1;               %  beta：域内元素的指引向量 
   
   A1_E=power(beta(A1+1)+1);                    %  将效验矩阵中的元素转换为本源元的指数形式表示
   A2_E=power(beta(A2+1)+1);
   
 b=zeros(1,q);
   for t=1:q-1  
       t_E=power(beta(t+1)+1);
       tmp=gfmul(t_E,A1_E,field);
       tmp=gfdiv(tmp,A2_E,field);
       if tmp == -Inf
          bb = 0;
          else
          bb = alpha(tmp + 2);       % 十进制
       end   
       b(t+1)=L1(t)+L2(bb);
   end
   
   xb=b(1);x2=b(2);
   xb=Max_x(xb,x2);
   for t=3:q
       x2=b(t);
       xb=Max_x(xb,x2);
   end
       
   
for i=1:q-1  %i就是公式里的i和ai
    
   a=zeros(1,q+1);
   i_E=power(beta(i+1)+1);
   
   A1_i_E=gfdiv(i_E,A1_E,field);
   A2_i_E=gfdiv(i_E,A2_E,field);
   
   if A1_i_E == -Inf
          A1_i = 0;
          else
          A1_i = alpha(A1_i_E + 2);    % 十进制
   end

   if A2_i_E == -Inf
          A2_i = 0;
          else
          A2_i = alpha(A2_i_E + 2);    % 十进制
   end
   a(1)=L1(A1_i);a(2)=L2(A2_i);
   
   for j=1:q-1             %j就是公式里的x
       j_E=power(beta(j+1)+1);
       if j~=A1_i 
           tmp=gfmul(j_E,A1_E,field);
           tmp=gfadd(tmp,i_E,field);
           tmp=gfdiv(tmp,A2_E,field);
           if tmp == -Inf
              aa = 0;
              else
              aa = alpha(tmp + 2);     % 十进制
           end 
           a(j+2)=L1(j)+L2(aa);
       end
   end
   a(A1_i+2)=[];
   
   xa=a(1);x2=a(2);
   xa=Max_x(xa,x2);
   for t=3:q
       x2=a(t);
       xa=Max_x(xa,x2);
   end
   L(i)=xa-xb;
end  
end

function [max_x]=Max_x(x1,x2)
% max*(x1,x2)=ln(e^x1+e^x2)=max(x1,x2)+ln(1+e^(-|x1-x2|))
% max_x=max(x1,x2)+log(1+exp(-abs(x1-x2)));
max_x=max(x1,x2);  % max*(x1,x2)近似为max(x1,x2)
end

3.判决的时候  译码迭代过程中各个节点之间传递的信息维数是q-1维，最后判决之前在最前面加一行全0行，因为符号为0的LLR为0，不参与译码，但是要参与判决。然后比较包含0的q个LLR的值，取最大对数似然比（LLR）所对应的符号值。