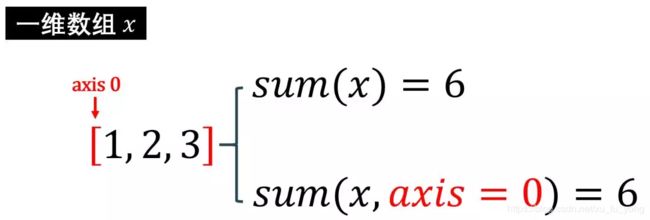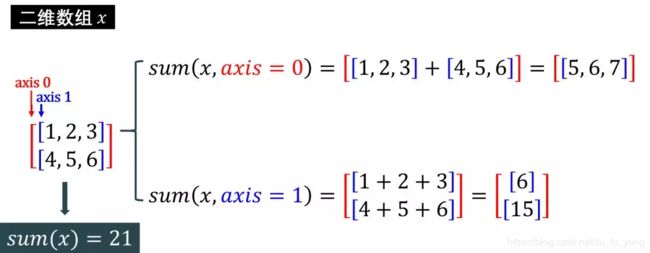Numpy基本使用
文章目录
- Numpy的基本使用
- 1、数组的创建
- 数组简介
- 创建数组
- 按步就班法
- 定隔定点法
- 一步登天法
- 数组的性质
- 一维数组
- 二维数组
- n 维数组
- 2、数组的存储和加载
- numpy自身的.npy格式
- 文本 .txt 格式
- 文本 .csv 格式
- 3、数组的获取
- 正规索引
- 布尔索引
- 花式索引
- 小结一下
- 4、数组的变形
- 重塑和打平
- 合并和分裂
- 重复和拼接
- 其他操作
- 5、数组的计算
- 元素层面计算
- 线性代数计算
- 元素整合计算
- 广播机制计算
- 总结
Numpy的基本使用
1、数组的创建
数组简介
数组 (array) 是相同类型的元素 (element) 的集合所组成数据结构 (data structure)。numpy 数组中的元素用的最多是「数值型」元素,平时我们说的一维、二维、三维数组长下面这个样子 (对应着线、面、体)。四维数组很难被可视化。
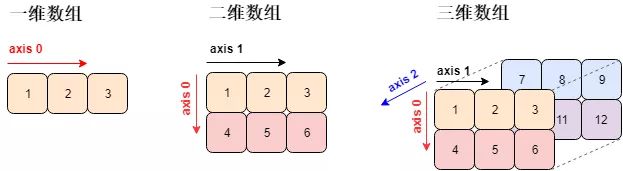
注意一个关键字 axis,中文叫「轴」,一个数组是多少维度就有多少根轴。由于 Python 计数都是从 0 开始的,那么
- 第 1 维度 = axis 0
- 第 2 维度 = axis 1
- 第 3 维度 = axis 2
但这些数组只可能在平面上打印出来,那么它们 (高于二维的数组) 的表现形式稍微有些不同。
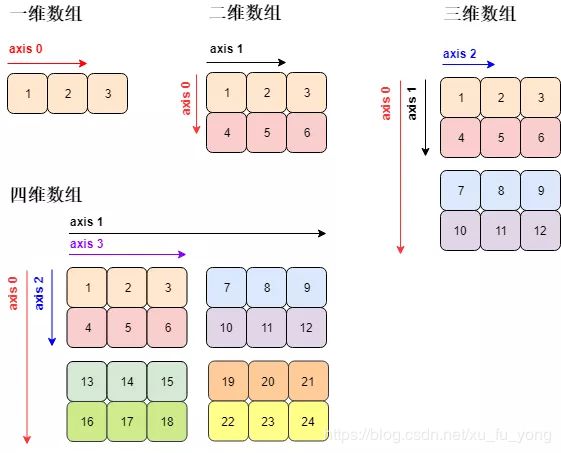
分析上图各个数组的在不同维度上的元素:
- 一维数组:轴 0 有 3 个元素
- 二维数组:轴 0 有 2 个元素,轴 1 有 3 个元素
- 三维数组:轴 0 有 2 个元素 (2 块),轴 1 有 2 个元素,轴 2 有 3 个元素
- 四维数组:轴 0 有 2 个元素 (2 块),轴 1 有 2 个元素 (2 块),轴 2 有 2 个元素,轴 3 有 3 个元素
创建数组
带着上面这个对轴的认识,接下来我们用代码来创建 numpy 数组,有三种方式:
- 按步就班的 np.array() 用在列表和元组上
- 定隔定点的 np.arange() 和 np.linspace()
- 一步登天的 np.ones(), np.zeros(), np.eye() 和 np.random.random()
按步就班法
给了「列表」和「元组」原材料,用 np.array() 包装一下便得到 numpy 数组。
import numpy as np
l = [3.5, 5, 2, 7, 9]
np.array(l)
array([3.5, 5. , 2. , 7. , 9. ])
t = (3.5, 5, 2, 8, 4.2)
np.array(t) #注意,numpy 数组的输出都带有 array() 的字样,里面的元素用「中括号 []」框住。
array([3.5, 5. , 2. , 8. , 4.2])
定隔定点法
更常见的两种创建 numpy 数组方法:
- 定隔的 arange:固定元素大小间隔
- 定点的 linspace:固定元素个数
函数 arange 的参数为起点 , 终点 , 间隔
其中 stop 必须要有,start 和 step 没有的话默认为 1。对着这个规则看看上面各种情况的输出。
注:用函数 print 打印 numpy 数组就没有 array() 的字样了,只用其内容,而且元素之间的「逗号」也没有了。
print(np.arange(8))
print(np.arange(2, 8))
print(np.arange(2, 8, 2))
[0 1 2 3 4 5 6 7]
[2 3 4 5 6 7]
[2 4 6]
函数 linspace 的参数为起点 , 终点 , 点数
linspace (start , stop , num)
其中 start 和 stop 必须要有,num 没有的话默认为 50。对着这个规则看看上面各种情况的输出。
print(np.linspace(2, 6, 3)) # 均分为三个
t = np.linspace(3, 8, 11)
print(np.linspace(3, 8, 11))
t
[2. 4. 6.]
[3. 3.5 4. 4.5 5. 5.5 6. 6.5 7. 7.5 8. ]
array([3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5, 7. , 7.5, 8. ])
一步登天法
NumPy 还提供一次性
-
用 zeros() 创建全是 0 的 n 维数组
-
用 ones() 创建全是 1 的 n 维数组
-
用 random() 创建随机 n 维数组
-
用 eye() 创建对角矩阵 (二维数组)
对于前三种,由于输出是 n 为数组,它们的参数是一个「标量」或「元组类型的形状」,下面三个例子一看就懂了:
print(np.zeros(5))
print(np.ones((2, 3)))
print(np.random.random((2, 3, 4)))
[0. 0. 0. 0. 0.]
[[1. 1. 1.]
[1. 1. 1.]]
[[[0.22776412 0.72046211 0.29758594 0.0923665 ]
[0.2027479 0.53507183 0.61219788 0.50821071]
[0.62908069 0.6038276 0.53519934 0.10484686]]
[[0.20239382 0.34965616 0.22142288 0.56592552]
[0.32693076 0.09853307 0.49262424 0.96626366]
[0.4547175 0.63994587 0.2033189 0.40908813]]]
对于函数 eye(),它的参数就是一个标量,控制矩阵的行数或列数:
此外还可以设定 eye() 里面的参数 k
-
默认设置 k = 0 代表 1 落在对角线上
-
k = 1 代表 1 落在对角线右上方
-
k = -1 代表 1 落在对角线左下方
np.eye(4)
print(np.eye(4, k=1))
np.eye(4, k=-1)
[[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]
[0. 0. 0. 0.]]
array([[0., 0., 0., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.]])
数组的性质
一维数组
用按步就班的 np.array() 带列表生成数组 arr
现在你应该会用 dir(arr) 来查看数组的属性了吧,看完之后我们对 type, ndim, len(), size, shape, stride, dtype 几个感兴趣,一一打印出来看看:
arr = np.array([3.5, 5, 2, 8, 4.2])
print('The type is:', type(arr))
print('The dimension is:', arr.ndim)
print('The length is:', len(arr))
print('The number of elements is:', arr.size)
print('The shape of array is:', arr.shape)
print('The stride of array is:', arr.strides)
print('The type of elements is:', arr.dtype)
The type is:
The dimension is: 1
The length is: 5
The number of elements is: 5
The shape of array is: (5,)
The stride of array is: (8,)
The type of elements is: float64
根据结果我们来看看上面属性到底是啥:
-
type:数组类型,当然是 numpy.ndarray
-
ndim:维度个数是 1
-
len():数组长度为 5 (注意这个说法只对一维数组有意义)
-
size:数组元素个数为 5
-
shape:数组形状,即每个维度的元素个数 (用元组来表示),只有一维,元素个数为 5,写成元组形式是 (5,)
-
strides:跨度,即在某一维度下为了获取到下一个元素需要「跨过」的字节数 (用元组来表示),float64 是 8 个字节数 (bytes),因此跨度为 8
-
dtype:数组元素类型,是双精度浮点 (注意和 type 区分)
注意我黄色高亮了 strides,这个概念对于解决引言的「转置高维数组」问题很重要。一图胜千言。
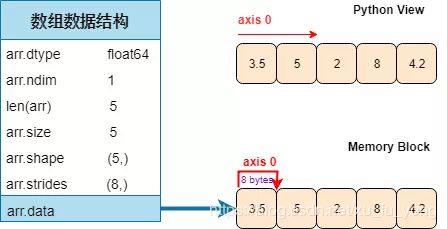
对一维数组来说,「Python 视图」看它和「内存块」存储它的形式是一样的.
二维数组
先用按步就班的 np.array() 带二维列表生成二维数组 arr2d按步就班的 np.array() 带二维列表生成二维数组 arr2d
l2 = [[1, 2, 3], [4, 5, 6]]
arr2d = np.array(l2)
arr2d
array([[1, 2, 3],
[4, 5, 6]])
print("The typeis :", type(arr2d))
print("The dimension is:", arr2d.ndim)
print("The length of array is:", len(arr2d))
print("The number of elments is:", arr2d.size)
print("The shape of array is:", arr2d.shape)
print("The stride of array is:", arr2d.strides)
print("The type of elements is:", arr2d.dtype)
The typeis :
The dimension is: 2
The length of array is: 2
The number of elments is: 6
The shape of array is: (2, 3)
The stride of array is: (12, 4)
The type of elements is: int32
同样,我们来分析一下上面属性:
-
type:数组类型 numpy.ndarray
-
ndim:维度个数是 2
-
len():数组长度为 2 (严格定义 len 是数组在「轴 0」的元素个数)
-
size:数组元素个数为 6
-
shape:数组形状 (2, 3)
-
strides:跨度 (12, 4) 看完下图再解释
-
dtype:数组元素类型 int32
对于二维数组,Python 视图」看它和「内存块」存储它的形式是不一样的,如下图所示:
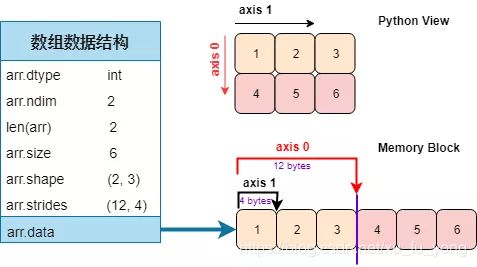
在 numpy 数组中,默认的是行主序 (row-major order),意思就是每行的元素在内存块中彼此相邻,而列主序 (column-major order) 就是每列的元素在内存块中彼此相邻。
回顾跨度 (stride) 的定义,即在某一维度下为了获取到下一个元素需要「跨过」的字节数。注:每一个 int32 元素是 4 个字节数。对着上图:
第一维度 (轴 0):沿着它获取下一个元素需要跨过 3 个元素,即 12 = 3×4 个字节
第二维度 (轴 1):沿着它获取下一个元素需要跨过 1 个元素,即 4 = 1×4 个字节
因此该二维数组的跨度为 (12, 4)。
n 维数组
我们使用np.random.random()来生成一个多维数组
arr4d = np.random.random((2, 2, 2, 3))
print("The type is:", type(arr4d))
print("The dimension is:", arr4d.ndim)
print("The length of array is:", len(arr4d))
print("The number of elments is:", arr4d.size)
print("The shape of array is:", arr4d.shape)
print("The stride of array is:", arr4d.strides)
print("The type of elments is:", arr4d.dtype)
arr4d
The type is:
The dimension is: 4
The length of array is: 2
The number of elments is: 24
The shape of array is: (2, 2, 2, 3)
The stride of array is: (96, 48, 24, 8)
The type of elments is: float64
array([[[[0.12097602, 0.85898477, 0.16043155],
[0.87946725, 0.96358488, 0.4051294 ]],
[[0.65434255, 0.21199418, 0.68517886],
[0.53783086, 0.93971496, 0.14067768]]],
[[[0.93745553, 0.95048614, 0.81013165],
[0.36328647, 0.16424842, 0.96708327]],
[[0.90332958, 0.30356389, 0.50146022],
[0.05044289, 0.49204122, 0.2607904 ]]]])
这里的stride是(96, 48, 24, 8)注意:一个float64的元素占8个字节
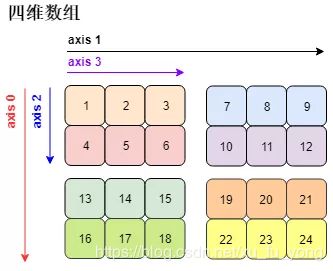
跨度 (stride) 的定义,即在某一维度下为了获取到下一个元素需要「跨过」的字节数。注:每一个 float64 元素是 8 个字节数
-
第一维度 (轴 0):沿着它获取下一个元素需要跨过 12 个元素,即 96 = 12×8 个字节
-
第二维度 (轴 1):沿着它获取下一个元素需要跨过 6 个元素,即 48 = 6×8 个字节
-
第三维度 (轴 2):沿着它获取下一个元素需要跨过 3 个元素,即 24 = 3×8 个字节
-
第四维度 (轴 3):沿着它获取下一个元素需要跨过 1 个元素,即 8 = 1×8 个字节
因此该四维数组的跨度为 (96, 48, 24, 8)。
2、数组的存储和加载
假设你已经训练完一个深度神经网络,该网络就是用无数参数来表示的。比如权重都是 numpy 数组,为了下次不用训练而重复使用,将其保存成 .npy 格式或者 .csv 格式是非常重要的。
numpy自身的.npy格式
用 np.save 函数将 numpy 数组保存为 .npy 格式,具体写法如下:
arr_disk = np.arange(8)
np.save("arr_disk", arr_disk)
arr_disk
array([0, 1, 2, 3, 4, 5, 6, 7])
arr_disk.npy 保存在 Jupyter Notebook 所在的根目录下。要加载它也很简单,用 np.load( “文件名” ) 即可:
np.load("arr_disk.npy")
array([0, 1, 2, 3, 4, 5, 6, 7])
文本 .txt 格式
用 np.savetxt 函数将 numpy 数组保存为 .txt 格式,具体写法如下:
arr_text = np.array([[1., 2., 3.],[4., 5., 6.]])
np.savetxt("arr_from_text.txt", arr_text)
用 np.loadtxt( “文件名” ) 即可加载该文件
np.loadtxt("arr_from_text.txt")
array([[1., 2., 3.],
[4., 5., 6.]])
文本 .csv 格式
arr_csv = np.array([[1., 2., 3.],[4., 5., 6.]])
np.savetxt("arr_csv.csv", arr_csv, delimiter=';')
用 np.genfromtxt( “文件名” ) 即可加载该文件
带上「分隔符 ;」
np.genfromtxt("arr_csv.csv", delimiter=';')
array([[1., 2., 3.],
[4., 5., 6.]])
3、数组的获取
获取数组是通过索引 (indexing) 和切片 (slicing) 来完成的,
-
切片是获取一段特定位置的元素
-
索引是获取一个特定位置的元素
索引和切片的方式和列表一模一样。对于一维数组 arr,
-
切片写法是 arr[start : stop : step]
-
索引写法是 arr[index]
因此,切片的操作是可以用索引操作来实现的 (一个一个总能凑成一段),只是没必要罢了。为了简化,我们在本章三节标题里把切片和索引都叫做索引。
索引数组有三种形式,正规索引 (normal indexing)、布尔索引 (boolean indexing) 和花式索引 (fancy indexing)。
正规索引
虽然切片操作可以由多次索引操作替代,但两者最大的区别在于
-
切片得到的是原数组的一个视图 (view) ,修改切片中的内容会改变原数组
-
索引得到的是原数组的一个复制 (copy),修改索引中的内容不会改变原数组
请看下面一维数组的例子来说明上述两者的不同。
一维数组
arr = np.arange(10)
arr
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
a = arr[6]
a = 100
arr
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
b = arr[5:8]
b[1] = 12
arr
array([ 0, 1, 2, 3, 4, 5, 12, 7, 8, 9])
这就证实了切片得到原数组的视图 (view),更改切片数据会更改原数组,而索引得到原数组的复制 (copy), 更改索引数据不会更改原数组。希望用下面一张图可以明晰 view 和 copy 的关系。
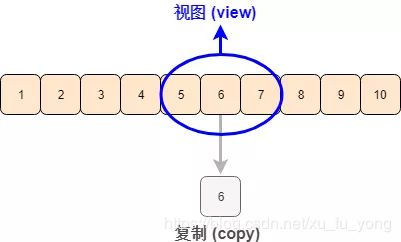
二维数组
arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
arr2d
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
索引的使用
#情况一:用 arr2d[2] 来索引第三行,更严格的说法是索引「轴 0」上的第三个元素。
arr2d[2]
array([7, 8, 9])
#情况二:用 arr2d[0][2] 来索引第一行第三列
arr2d[0][2]
arr2d[0, 2]
3
切片的使用
# 情况一:用 arr2d[:2] 切片前两行,更严格的说法是索引「轴 0」上的前两个元素。
arr2d[:2]
array([[1, 2, 3],
[4, 5, 6]])
#情况二:用 arr2d[:, [0,2]] 切片第一列和第三列
arr2d[:, [0, 2]]
array([[1, 3],
[4, 6],
[7, 9]])
# 情况三:用 arr2d[1, :2] 切片第二行的前两个元素
arr2d[1, :2]
array([4, 5])
#情况四:用 arr2d[:2, 2] 切片第三列的前两个元素
arr2d[:2, 2]
array([3, 6])
布尔索引
布尔索引,就是用一个由布尔 (boolean) 类型值组成的数组来选择元素的方法。
假设我们有阿里巴巴 (BABA),脸书 (FB) 和京东 (JD) 的
-
股票代码 code 数组
-
股票价格 price 数组:每行记录一天开盘,最高和收盘价格。
code = np.array(['BABA', 'FB', 'JD', 'BABA', 'JD', 'FB'])
price = np.array([[170,177,169],[150,159,153],
[24,27,26],[165,170,167],
[22,23,20],[155,116,157]])
假设我们想找出 BABA 对应的股价,首先找到 code 里面是 ‘BABA’ 对应的索引 (布尔索引),即一个值为 True 和 False 的布尔数组。
code == 'BABA'
array([ True, False, False, True, False, False])
用该索引可以获取 BABA 的股价:
price[code == 'BABA']
array([[170, 177, 169],
[165, 170, 167]])
用该索引还可以获取 BABA 的最高和收盘价格:
price[code =='BABA', 1:]
array([[177, 169],
[170, 167]])
试试把股价小于 25 的清零。
price[price < 25] = 0
price
array([[170, 177, 169],
[150, 159, 153],
[ 0, 27, 26],
[165, 170, 167],
[ 0, 0, 0],
[155, 116, 157]])
花式索引
花式索引是获取数组中想要的特定元素的有效方法。考虑下面数组:
arr = np.arange(32).reshape(8, 4)
arr
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23],
[24, 25, 26, 27],
[28, 29, 30, 31]])
假设你想按特定顺序来获取第 5, 4 和 7 行时,用 arr[ [4,3,6] ]
arr[[4, 3, 6]]
array([[16, 17, 18, 19],
[12, 13, 14, 15],
[24, 25, 26, 27]])
假设你想按特定顺序来获取倒数第 4, 3 和 6 行时 (即正数第 4, 5 和 2 行),用 arr[ [-4,-3,-6] ]
arr[[-4, -3, -6]]
array([[16, 17, 18, 19],
[20, 21, 22, 23],
[ 8, 9, 10, 11]])
此外,你还能更灵活的设定「行」和「列」中不同的索引,如下
arr[[1, 5, 7, 2],[0, 3, 1, 2]]
array([ 4, 23, 29, 10])
最后,我们可以交换列,把原先的 [0,1,2,3] 的列换成 [0,3,1,2]。
arr[:, [0, 3, 1, 2]]
array([[ 0, 3, 1, 2],
[ 4, 7, 5, 6],
[ 8, 11, 9, 10],
[12, 15, 13, 14],
[16, 19, 17, 18],
[20, 23, 21, 22],
[24, 27, 25, 26],
[28, 31, 29, 30]])
小结一下
数组创建、数组存载和数组获取。同样把 numpy 数组当成一个对象,要学习它,无非就是学习怎么
-
创建它:按步就班法、定隔定点法、一步登天法
-
存载它:保存成 .npy, .txt 和 .csv 格式,下次加载即用
-
获取它:一段用切片,一个用索引;有正规法、布尔法、花式法
接下来学习一下NumPy 的其他硬核操作
-
变形它:重塑和打平,合并和分裂,元素重复和数组重复
-
计算它:元素层面计算,线性代数计算,广播机制计算
先说一下数组转置的问题
arr = np.arange(16).reshape((2, 2, 4))
arr
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
数组转置的本质:交换每个轴 (axis) 的形状 (shape) 和跨度 (stride)。
将第 1, 2, 3 维度转置到第 2, 1, 3 维度,即将轴 0, 1, 2 转置到轴 1, 0, 2。
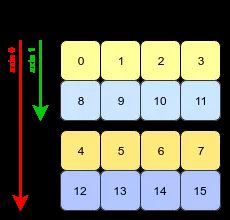
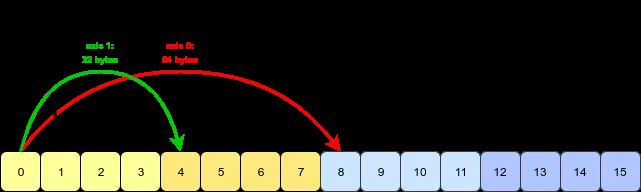
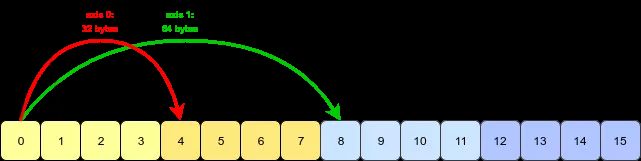
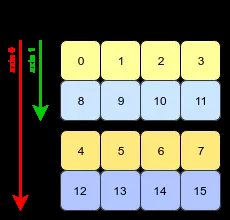
arr.transpose(2, 0, 1)
array([[[ 0, 4],
[ 8, 12]],
[[ 1, 5],
[ 9, 13]],
[[ 2, 6],
[10, 14]],
[[ 3, 7],
[11, 15]]])
arr.shape
(2, 2, 4)
arr.strides
(32, 16, 4)
4、数组的变形
四大类数组层面上的操作,具体有
-
1.重塑 (reshape) 和打平 (ravel, flatten)
-
2.合并 (concatenate, stack) 和分裂 (split)
-
3.重复 (repeat) 和拼接 (tile)
-
4.其他操作 (sort, insert, delete, copy)
重塑和打平
重塑 (reshape) 和打平 (ravel, flatten) 这两个操作仅仅只改变数组的维度
-
重塑是从低维到高维
-
打平是从高维到低维
重塑
用reshape()函数将一维数组 arr 重塑成二维数组。
arr = np.arange(12)
print(arr.reshape((4, 3)))
print(arr)
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
[ 0 1 2 3 4 5 6 7 8 9 10 11]
当你重塑高维矩阵时,不想花时间算某一维度的元素个数时,可以用「-1」取代,程序会自动帮你计算出来。比如把 12 个元素重塑成 (2, 6),你可以写成 (2,-1) 或者 (-1, 6)。
print(arr.reshape((2, -1)))
print(arr.reshape((-1, 6)))
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
打平
用 ravel() 或flatten() 函数将二维数组 arr 打平成一维数组。
arr = np.arange(12).reshape((4, 3))
print(arr)
revel_arr = arr.ravel()
print(revel_arr)
flatten_arr = arr.flatten()
print(flatten_arr)
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
[ 0 1 2 3 4 5 6 7 8 9 10 11]
[ 0 1 2 3 4 5 6 7 8 9 10 11]
思考:为什么打平后的数组不是
[ 0 3 6 9 1 4 7 10 2 5 8 11 ]
要回答这个问题,需要了解 numpy 数组在内存块的存储方式。
行主序和列主序
行主序 (row-major order) 指每行的元素在内存块中彼此相邻,而列主序 (column-major order) 指每列的元素在内存块中彼此相邻。
在众多计算机语言中,
-
默认行主序的有 C 语言(下图 order=‘C’ 等价于行主序)
-
默认列主序的有 Fortran 语言(下图 order=‘F’ 等价于列主序)
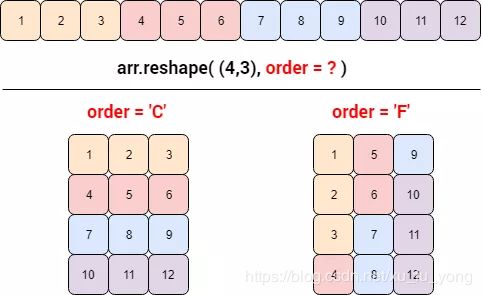
在 numpy 数组中,默认的是行主序,即 order =‘C’。现在可以回答本节那两个问题了。
如果你真的想在「重塑」和「打平」时用列主序,只用把 order 设为 ‘F’,以重塑举例:
print(arr.reshape((4, 3), order='F'))
print(arr.flatten(order='F'))
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
[ 0 3 6 9 1 4 7 10 2 5 8 11]
两个函数 ravel() flatten()它们的区别在哪里?
函数 ravel() 或 flatten() 的不同之处是
-
1.ravel() 按「行主序」打平时没有复制原数组,按「列主序」在打平时复制了原数组
-
2.flatten() 在打平时复制了原数组
用代码验证一下,首先看 flatten(),将打平后的数组 flatten 第一个元素更新为 10000,并没有对原数组 arr 产生任何影响 (证明 flatten() 是复制了原数组)
arr = np.arange(6).reshape(2,3)
print( arr )
flatten = arr.flatten()
print( flatten )
flatten_arr[0] = 10000
print( arr )
[[0 1 2]
[3 4 5]]
[0 1 2 3 4 5]
[[0 1 2]
[3 4 5]]
再看 ravel() 在「列主序」打平,将打平后的数组 ravel_F 第一个元素更新为 10000,并没有对原数组 arr 产生任何影响 (证明 ravel(order=‘F’) 是复制了原数组)
ravel_F = arr.ravel( order='F' )
ravel_F[0] = 10000
print( ravel_F )
print( arr )
[10000 3 1 4 2 5]
[[0 1 2]
[3 4 5]]
最后看 ravel() 在「行主序」打平,将打平后的数组 ravel_C 第一个元素更新为 10000,原数组 arr[0][0] 也变成了 10000 (证明 ravel() 没有复制原数组)
ravel_C = arr.ravel()
ravel_C[0] = 10000
print( ravel_C )
print( arr )
[10000 1 2 3 4 5]
[[10000 1 2]
[ 3 4 5]]
合并和分裂
合并 (concatenate, stack) 和分裂 (split) 这两个操作仅仅只改变数组的分合
-
合并是多合一
-
分裂是一分多
使用「合并」函数有三种选择
-
1.有通用的 concatenate
-
2.有专门的 vstack, hstack, dstack
-
3.有极简的 r_, c_
用下面两个数组来举例:
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
concatenate
在 concatenate() 函数里通过设定轴,来对数组进行竖直方向合并 (轴 0) 和水平方向合并 (轴 1)。
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
array([[ 1, 2, 3, 7, 8, 9],
[ 4, 5, 6, 10, 11, 12]])
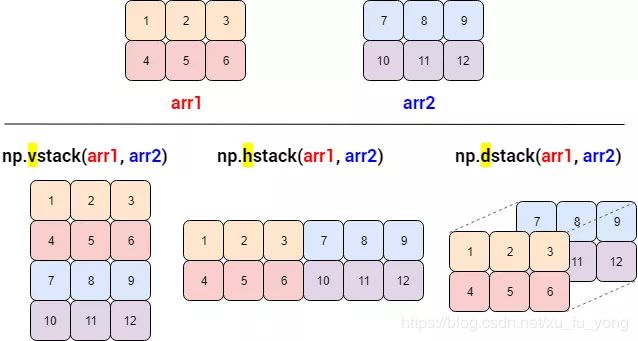
vstack, hstack, dstack
通用的东西是好,但是可能效率不高,NumPy 里还有专门合并的函数
-
vstack:v 代表 vertical,竖直合并,等价于 concatenate(axis=0)
-
hstack:h 代表 horizontal,水平合并,等价于 concatenate(axis=1)
-
dstack:d 代表 depth-wise,按深度合并,深度有点像彩色照片的 RGB 通道
一图胜千言:
print(np.vstack((arr1, arr2)))
print(np.hstack((arr1, arr2)))
print(np.dstack((arr1, arr2)))
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
[[ 1 2 3 7 8 9]
[ 4 5 6 10 11 12]]
[[[ 1 7]
[ 2 8]
[ 3 9]]
[[ 4 10]
[ 5 11]
[ 6 12]]]
和 vstack, hstack 不同,dstack 将原数组的维度增加了一维。
np.dstack((arr1, arr2)).shape
(2, 3, 2)
r_, c_
此外,还有一种更简单的在竖直和水平方向合并的函数,r_() 和 c_()。
print(np.r_[arr1, arr2])
print(np.c_[arr1, arr2])
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
[[ 1 2 3 7 8 9]
[ 4 5 6 10 11 12]]
除此之外,r_() 和 c_() 有什么特别之处么?(如果完全和 vstack() 和hstack() 一样,那也没有存在的必要了)
- 参数可以是切片。
print(np.r_[-2:2:1,[0]*3,5,6]) #-2-2 + 3个0+ 5,6
[-2 -1 0 1 0 0 0 5 6]
- 第一个参数可以是控制参数,如果它用 ‘r’ 或 ‘c’ 字符可生成线性代数最常用的 matrix (和二维 numpy array 稍微有些不同)
np.r_['r', [1, 2, 3],[4, 5, 6]]
matrix([[1, 2, 3, 4, 5, 6]])
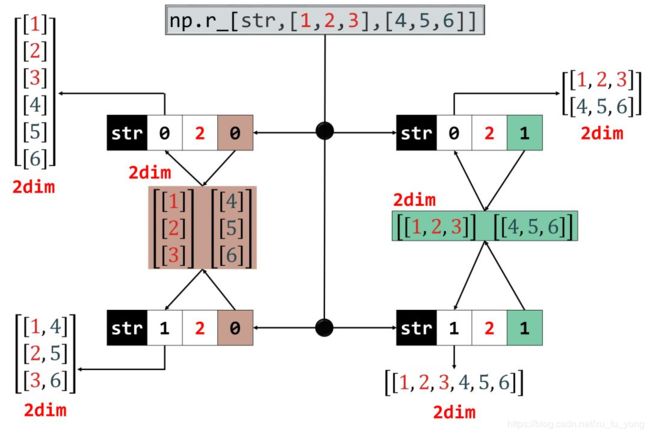
- 第一个参数可以是控制参数,如果它写成 ‘a,b,c’ 的形式,其中
a:代表轴,按「轴 a」来合并
b:合并后数组维度至少是 b
c:在第 c 维上做维度提升
print( np.r_['0,2,0', [1,2,3], [4,5,6]] )
print( np.r_['0,2,1', [1,2,3], [4,5,6]] )
print( np.r_['1,2,0', [1,2,3], [4,5,6]] )
print( np.r_['1,2,1', [1,2,3], [4,5,6]] )
[[1]
[2]
[3]
[4]
[5]
[6]]
[[1 2 3]
[4 5 6]]
[[1 4]
[2 5]
[3 6]]
[[1 2 3 4 5 6]]
现在可以看出字符串 ‘a,b,c’ 的 b 起的作用,完事后的维度是 2。看个图:
字符串 ‘a,b,c’ 总共有四类,分别是
-
‘0, 2, 0’
-
‘0, 2, 1’
-
‘1, 2, 0’
-
‘1, 2, 1’
函数里两个数组 [1,2,3], [4,5,6] 都是一维
-
c = 0 代表在「轴 0」上升一维,因此得到 [[1],[2],[3]] 和 [[4],[5],[6]]
-
c = 1 代表在「轴 1」上升一维,因此得到 [[1,2,3]] 和 [[4,5,6]]
接下来如何合并就看 a 的值了
-
a = 0, 沿着「轴 0」合并
-
a = 1, 沿着「轴 1」合并
分裂
使用「分裂」函数有两种选择
-
有通用的 split
-
有专门的 hsplit, vsplit
用下面数组来举例:
arr = np.arange(25).reshape((5, 5))
print(arr)
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]
[15 16 17 18 19]
[20 21 22 23 24]]
和 concatenate() 函数一样,我们可以在 split() 函数里通过设定轴,来对数组沿着竖直方向分裂 (轴 0) 和沿着水平方向分裂 (轴 1)。
first, second, third = np.split(arr, [1,3])
print('The first split is:', first)
print('The second split is:', second)
print('The third split is:', third)
The first split is: [[0 1 2 3 4]]
The second split is: [[ 5 6 7 8 9]
[10 11 12 13 14]]
The third split is: [[15 16 17 18 19]
[20 21 22 23 24]]
split() 默认沿着轴 0 分裂,其第二个参数 [1, 3] 相当于是个切片操作,将数组分成三部分:
-
第一部分 - :1 (即第 1 行)
-
第二部分 - 1:3 (即第 2 到 3 行)
-
第三部分 - 3: (即第 4 到 5 行)
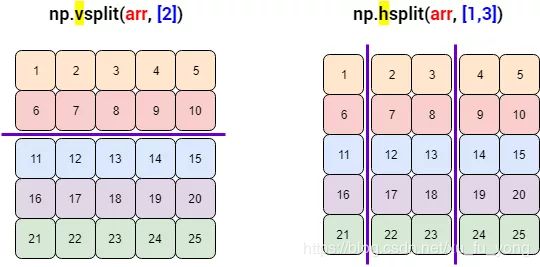
hsplit, vsplit
vsplit() 和 split(axis=0) 等价,hsplit() 和 split(axis=1) 等价。一图胜千言:
first, second, third = np.hsplit(arr,[1,3])
print( 'The first split is', first )
print( 'The second split is', second )
print( 'The third split is', third )
The first split is [[ 0]
[ 5]
[10]
[15]
[20]]
The second split is [[ 1 2]
[ 6 7]
[11 12]
[16 17]
[21 22]]
The third split is [[ 3 4]
[ 8 9]
[13 14]
[18 19]
[23 24]]
重复和拼接
重复 (repeat) 和拼接 (tile) 这两个操作本质都是复制
-
重复是在元素层面复制
-
拼接是在数组层面复制
重复
函数 repeat() 复制的是数组的每一个元素,参数有几种设定方法:
-
一维数组:用标量和列表来控制复制元素的个数
-
多维数组:用标量和列表来控制复制元素的个数,用轴来控制复制的行和列
标量
标量参数 3 - 数组 arr 中每个元素复制 3 遍。
arr = np.arange(3)
print(arr)
print(arr.repeat(3))
[0 1 2]
[0 0 0 1 1 1 2 2 2]
列表
列表参数 [2,3,4] - 数组 arr 中每个元素分别复制 2, 3, 4 遍。
print(arr.repeat([2, 3, 4]))
[0 0 1 1 1 2 2 2 2]
标量和轴
标量参数 2 和轴 0 - 数组 arr2d 中每个元素沿着轴 0 复制 2 遍。
arr2d = np.arange(6).reshape((2, 3))
print(arr2d)
print(arr2d.repeat(2, axis=0))
[[0 1 2]
[3 4 5]]
[[0 1 2]
[0 1 2]
[3 4 5]
[3 4 5]]
列表和轴
列表参数 [2,3,4] 和轴 1 - 数组 arr2d 中每个元素沿着轴 1 分别复制 2, 3, 4 遍。
print(arr2d.repeat([2, 3, 4], axis=1))
[[0 0 1 1 1 2 2 2 2]
[3 3 4 4 4 5 5 5 5]]
拼接
函数 tile() 复制的是数组本身,参数有几种设定方法:
-
标量:把数组当成一个元素,一列一列复制
-
形状:把数组当成一个元素,按形状复制
标量
标量参数 2 - 数组 arr 按列复制 2 遍。
arr2d = np.arange(6).reshape((2, 3))
print(arr2d)
print(np.tile(arr2d, 2))
[[0 1 2]
[3 4 5]]
[[0 1 2 0 1 2]
[3 4 5 3 4 5]]
形状
标量参数 (2,3) - 数组 arr 按形状复制 6 (2×3) 遍,并以 (2,3) 的形式展现。
print(np.tile(arr2d, (2, 3)))
[[0 1 2 0 1 2 0 1 2]
[3 4 5 3 4 5 3 4 5]
[0 1 2 0 1 2 0 1 2]
[3 4 5 3 4 5 3 4 5]]
其他操作
数组的其他操作,包括排序 (sort),插入 (insert),删除 (delete) 和复制 (copy)。
排序
排序包括直接排序 (direct sort) 和间接排序 (indirect sort)。
直接排序
sort()函数是按升序 (ascending order) 排列的,该函数里没有参数可以控制 order
arr = np.array([5, 3, 2, 6, 1, 4])
print("Before sorting:",arr)
arr.sort()
print("After sorting:", arr)
Before sorting: [5 3 2 6 1 4]
After sorting: [1 2 3 4 5 6]
区别
用来排序 numpy 用两种方式:
arr.sort()
np.sort( arr )
第一种 sort 会改变 arr,第二种 sort 在排序时创建了 arr 的一个复制品,不会改变 arr。看下面代码,用一个形状是 (3, 4) 的「二维随机整数」数组来举例,用整数是为了便于读者好观察排序前后的变化:
arr = np.random.randint(40, size=(3, 4))
print(arr)
arr[:, 0].sort()
print(arr)
np.sort(arr[:, 1])
print(arr)
[[26 7 37 22]
[12 9 13 32]
[33 15 21 17]]
[[12 7 37 22]
[26 9 13 32]
[33 15 21 17]]
[[12 7 37 22]
[26 9 13 32]
[33 15 21 17]]
此外也可以在不同的轴上排序,对于二维数组,在「轴 0」上排序是「跨行」排序,在「轴 1」上排序是「跨列」排序。
arr.sort(axis=1)
print(arr)
[[ 7 12 22 37]
[ 9 13 26 32]
[15 17 21 33]]
间接排序
有时候我们不仅仅只想排序数组,还想在排序过程中提取每个元素在原数组对应的索引(index),这时 argsort() 就派上用场了。以排列下面五个学生的数学分数为例:
score = np.array([100, 60, 99, 80, 91])
idx = score.argsort()
print(idx)
[1 3 4 2 0]
这个 idx = [1 3 4 2 0] 怎么理解呢?很简单,排序完之后分数应该是 [60 80 91 99 100],
-
60,即 score[1] 排在第0位, 因此 idx[0] =1
-
80,即 score[3] 排在第1 位, 因此 idx[1] =3
-
91,即 score[4] 排在第2 位, 因此 idx[2] =4
-
99,即 score[2] 排在第3 位, 因此 idx[3] =2
-
100,即 score[0] 排在第4 位, 因此 idx[4] =0
用这个 idx 对 score 做一个「花式索引」得到
print(score[idx])
[ 60 80 91 99 100]
看一个二维数组的例子。
对其第一行 arr[0] 排序,获取索引,在应用到所用行上。
arr = np.random.randint(40, size=(3, 4))
print(arr)
arr[:, arr[0].argsort()]
[[27 14 7 20]
[ 6 7 8 1]
[ 0 23 20 16]]
array([[ 7, 14, 20, 27],
[ 8, 7, 1, 6],
[20, 23, 16, 0]])
插入和删除
和列表一样,我们可以给 numpy 数组
-
用insert()函数在某个特定位置之前插入元素
-
用delete()函数删除某些特定元素
a = np.arange(6)
print(a)
print(np.insert(a, 1, 100))
print(np.delete(a, [1, 3]))
[0 1 2 3 4 5]
[ 0 100 1 2 3 4 5]
[0 2 4 5]
复制
用copy()函数来复制数组 a 得到 a_copy,很明显,改变 a_copy 里面的元素不会改变 a。
a = np.arange(6)
a_copy = a.copy()
print( 'Before changing value, a is', a )
print( 'Before changing value, a_copy is', a_copy )
a_copy[-1] = 99
print( 'After changing value, a is', a )
print( 'After changing value, a_copy is', a_copy )
Before changing value, a is [0 1 2 3 4 5]
Before changing value, a_copy is [0 1 2 3 4 5]
After changing value, a is [0 1 2 3 4 5]
After changing value, a_copy is [ 0 1 2 3 4 99]
5、数组的计算
介绍四大类数组计算,具体有
1.元素层面 (element-wise) 计算
2.线性代数 (linear algebra) 计算
3.元素整合 (element aggregation) 计算
4.广播机制 (broadcasting) 计算
元素层面计算
Numpy 数组元素层面计算包括:
-
二元运算 (binary operation):加减乘除
-
数学函数:倒数、平方、指数、对数
-
比较运算 (comparison)
先定义两个数组 arr1 和 arr2。
arr1 = np.array([[1., 2., 3.],[4., 5., 6.]])
arr2 = np.ones((2, 3)) * 2
print(arr1)
print(arr2)
[[1. 2. 3.]
[4. 5. 6.]]
[[2. 2. 2.]
[2. 2. 2.]]
#加、减、乘、除
print(arr1 + arr2 +1)
print(arr1 - arr2)
print(arr1 * arr2)
print(arr1 / arr2)
[[4. 5. 6.]
[7. 8. 9.]]
[[-1. 0. 1.]
[ 2. 3. 4.]]
[[ 2. 4. 6.]
[ 8. 10. 12.]]
[[0.5 1. 1.5]
[2. 2.5 3. ]]
#倒数、平方、指数、对数
print(1 / arr1)
print(arr1 ** 2)
print(np.exp(arr1))
print(np.log(arr1))
[[1. 0.5 0.33333333]
[0.25 0.2 0.16666667]]
[[ 1. 4. 9.]
[16. 25. 36.]]
[[ 2.71828183 7.3890561 20.08553692]
[ 54.59815003 148.4131591 403.42879349]]
[[0. 0.69314718 1.09861229]
[1.38629436 1.60943791 1.79175947]]
#比较
arr1 > arr2
array([[False, False, True],
[ True, True, True]])
arr1 > 3
array([[False, False, False],
[ True, True, True]])
从上面结果可知
-
「数组和数组间的二元运算」都是在元素层面上进行的
-
「作用在数组上的数学函数」都是作用在数组的元素层面上的。
-
「数组和数组间的比较」都是在元素层面上进行的
但是在「数组和标量间的比较」时,python 好像先把 3 复制了和 arr1 形状一样的数组 [[3,3,3], [3,3,3]],然后再在元素层面上作比较。上述这个复制标量的操作叫做「广播机制」,是 NumPy 里最重要的一个特点
线性代数计算
在机器学习、金融工程和量化投资的编程过程中,因为运行速度的要求,通常会向量化 (vectorization) 而涉及大量的线性代数运算,尤其是矩阵之间的乘积运算。
但是,在 NumPy 默认不采用矩阵运算,而是数组 (ndarray) 运算。矩阵只是二维,而数组可以是任何维度,因此数组运算更通用些。
如果你非要二维数组 arr2d 进行矩阵运算,那么可以通过调用以下函数来实现:
-
A = np.mat(arr2d)
-
A = np.asmatrix(arr2d)
下面我们分别对「数组」和「矩阵」从创建、转置、求逆和相乘四个方面看看它们的同异。
创建
创建数组 arr2d 和矩阵 A,注意它们的输出有 array 和 matrix 的关键词。
arr2d = np.array([[1, 2], [3, 1]])
arr2d
array([[1, 2],
[3, 1]])
A = np.asmatrix(arr2d)
A
matrix([[1, 2],
[3, 1]])
转置
数组用 arr2d.T 操作或 arr.tranpose() 函数,而矩阵用 A.T 操作。主要原因就是 .T 只适合二维数据.
print(arr2d.T)
print(arr2d.transpose())
print(A.T)
[[1 3]
[2 1]]
[[1 3]
[2 1]]
[[1 3]
[2 1]]
求逆
数组用 np.linalg.inv() 函数,而矩阵用 A.I 和 A**-1 操作。
print(np.linalg.inv(arr2d))
print(A.I)
print(A ** -1)
[[-0.2 0.4]
[ 0.6 -0.2]]
[[-0.2 0.4]
[ 0.6 -0.2]]
[[-0.2 0.4]
[ 0.6 -0.2]]
相乘
相乘是个很模棱两可的概念
-
数组相乘是在元素层面进行,
-
矩阵相乘就是数学定义的矩阵相乘 (比如第一个矩阵的列要和第二个矩阵的行一样)
看个例子,「二维数组」相乘「一维数组」,「矩阵」相乘「向量」,看看有什么有趣的结果。
首先定义「一维数组」arr 和 「列向量」b:
arr = np.array([1, 2])
b = np.asmatrix(arr).T
print(arr.shape, b.shape)
(2,) (2, 1)
由上面结果看出, arr 的形状是 (2,),只含一个元素的元组只说明 arr 是一维,数组是不分行数组或列数组的。而 b 的形状是 (2,1),显然是列向量。
相乘都是用 * 符号,
print(arr2d * arr)
print(A * b)
[[1 4]
[3 2]]
[[5]
[5]]
由上面结果可知,
-
二维数组相乘一维数组得到的还是个二维数组,解释它需要用到「广播机制」。现在大概知道一维数组 [1 2] 第一个元素 1 乘上 [1 3] 得到 [1 3],而第二个元素 2 乘上 [2 1] 得到 [4 2]。
-
而矩阵相乘向量的结果和我们学了很多年的线代结果很吻合。
再看一个例子,「二维数组」相乘「二维数组」,「矩阵」相乘「矩阵」
print(arr2d * arr2d)
[[1 4]
[9 1]]
print(A * A)
[[7 4]
[6 7]]
由上面结果可知,
-
虽然两个二维数组相乘得到二维数组,但不是根据数学上矩阵相乘的规则得来的,而且由元素层面相乘得到的。两个 [[1 2], [3,1]] 的元素相乘确实等于 [[1 4], [9,1]]。
-
而矩阵相乘矩阵的结果和我们学了很多年的线代结果很吻合。
问题来了,那么怎么才能在数组上实现「矩阵相乘向量」和「矩阵相乘矩阵」呢?用点乘函数 dot()。
print(np.dot(arr2d, arr))
print(np.dot(arr2d, arr2d))
[5 5]
[[7 4]
[6 7]]
结果对了,但还有一个小小的差异
-
矩阵相乘列向量的结果是个列向量,写成 [[5],[5]],形状是 (2,1)
-
二维数组点乘一维数组结果是个一维数组,写成 [5, 5],形状是 (2,)
由此我们来分析下 NumPy 里的 dot() 函数,计算数组和数组之间的点乘结果。
点乘函数
通常我们也把 n 维数组称为张量,点乘左右两边最常见的数组就是
-
向量 (1D) 和向量 (1D)
-
矩阵 (2D) 和向量 (1D)
-
矩阵 (2D) 和矩阵 (2D)
分别看看三个简单例子。
例一:np.dot(向量, 向量) 实际上做的就是内积,即把两个向量每个元素相乘,最后再加总。点乘结果 10 是个标量 (0D 数组),形状 = ()。
x = np.array([1, 2, 3])
y = np.array([3, 2, 1])
z = np.dot(x, y)
print(z.shape)
print(z)
()
10
例二:np.dot(矩阵, 向量) 实际上做的就是普通的矩阵乘以向量。点乘结果是个向量 (1D 数组),形状 = (2, )。
x = np.array( [1, 2, 3] )
y = np.array( [[3, 2, 1], [1, 1, 1]] )
z = np.dot(y,x)
print( z.shape )
print( z )
(2,)
[10 6]
例三:np.dot(矩阵, 矩阵) 实际上做的就是普通的矩阵乘以矩阵。点乘结果是个矩阵 (2D 数组),形状 = (2, 3)。
x = np.array( [[1, 2, 3], [1, 2, 3], [1, 2, 3]] )
y = np.array( [[3, 2, 1], [1, 1, 1]] )
z = np.dot(y,x)
print( z.shape )
print( z )
(2, 3)
[[ 6 12 18]
[ 3 6 9]]
从例二和例三看出,当 x 第二个维度的元素 (x.shape[1]) 和 y 第一个维度的元素 (y.shape[0]) 个数相等时,np.dot(X, Y) 才有意义,点乘得到的结果形状 = (X.shape[0], y.shape[1])。
上面例子都是低维数组 (维度 ≤ 2) 的点乘运算,接下来我们看两个稍微复杂的例子。
例四:当 x 是 3D 数组,y 是 1D 数组,np.dot(x, y) 是将 x 和 y 最后一维的元素相乘并加总。此例 x 的形状是 (2, 3, 4),y 的形状是 (4, ),因此点乘结果的形状是 (2, 3)。
x = np.ones( shape=(2, 3, 4) )
y = np.array( [1, 2, 3, 4] )
z = np.dot(x,y)
print( z.shape )
print( z )
(2, 3)
[[10. 10. 10.]
[10. 10. 10.]]
例五:当 x 是 3D 数组,y 是 2D 数组,np.dot(x, y) 是将 x 的最后一维和 y 的倒数第二维的元素相乘并加总。此例 x 的形状是 (2, 3, 4),y 的形状是 (4, 2),因此点乘结果的形状是 (2, 3, 2)。
x = np.random.normal( 0, 1, size=(2, 3, 4) )
y = np.random.normal( 0, 1, size=(4, 2) )
z = np.dot(x,y)
print( z.shape )
print( z )
(2, 3, 2)
[[[-0.57217256 -1.94300362]
[-1.37522899 -0.07997041]
[ 2.83326314 1.507684 ]]
[[-6.06152461 -1.9994237 ]
[-0.42940618 0.12096553]
[ 0.89521998 1.482201 ]]]
例五的规则也适用于 nD 数组和 mD 数组 (当 m ≥ 2 时) 的点乘。
元素整合计算
在数组中,元素可以以不同方式整合 (aggregation)。拿求和 (sum) 函数来说,我们可以对数组
-
所有的元素求和
-
在某个轴 (axis) 上的元素求和
先定义数组
arr = np.arange(1, 7).reshape((2, 3))
arr
array([[1, 2, 3],
[4, 5, 6]])
分别对全部元素、跨行 (across rows)、跨列 (across columns) 求和:
print( 'The total sum is', arr.sum() )
print( 'The sum across rows is', arr.sum(axis=0) )
print( 'The sum across columns is', arr.sum(axis=1) )
The total sum is 21
The sum across rows is [5 7 9]
The sum across columns is [ 6 15]
分析上述结果:
-
1, 2, 3, 4, 5, 6 的总和是 21
-
跨行求和 = [1 2 3] + [4 5 6] = [5 7 9]
-
跨列求和 = [1+2+3 4+5+6] = [6 15]
行和列这些概念对矩阵 (二维矩阵) 才适用,高维矩阵还是要用轴 (axis) 来区分每个维度。让我们抛弃「行列」这些特殊概念,拥抱「轴」这个通用概念来重看数组 (一到四维) 。
有了轴的概念,我们再来看看 sum() 求和函数。
一维数组
分析结果:
-
1, 2, 3 的总和是 6
-
在轴 0(只有一个轴) 上的元素求和是 6
用代码验证一下:
arr = np.array([1,2,3])
print( 'The total sum is', arr.sum() )
print( 'The sum on axis0 is', arr.sum(axis=0) )
The total sum is 6
The sum on axis0 is 6
二维数组
用代码验证一下:
arr = np.arange(1,7).reshape((2,3))
print( arr )
print( 'The total sum is', arr.sum() )
print( 'The sum on axis0 is', arr.sum(axis=0) )
print( 'The sum on axis1 is', arr.sum(axis=1) )
[[1 2 3]
[4 5 6]]
The total sum is 21
The sum on axis0 is [5 7 9]
The sum on axis1 is [ 6 15]
结果是对的,但是好像括号比上图推导出来的少一个。原因np.sum()里面有个参数是 keepdims,意思是「保留维度」,默认值时 False,因此会去除多余的括号,比如 [[5, 7, 9]] 会变成 [5, 7, 9]。
如果把 keepdims 设置为 True,那么打印出来的结果和上图推导的一模一样。
print( arr.sum(axis=0, keepdims=True) )
print( arr.sum(axis=1, keepdims=True) )
[[5 7 9]]
[[ 6]
[15]]
三维数组
用代码验证一下:
arr = np.arange(1,13).reshape((2,2,3))
print(arr)
print( 'The total sum is', arr.sum() )
print( 'The sum on axis0 is', arr.sum(axis=0) )
print( 'The sum on axis1 is', arr.sum(axis=1) )
print( 'The sum on axis2 is', arr.sum(axis=2) )
[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]]
The total sum is 78
The sum on axis0 is [[ 8 10 12]
[14 16 18]]
The sum on axis1 is [[ 5 7 9]
[17 19 21]]
The sum on axis2 is [[ 6 15]
[24 33]]
打印出来的结果比上图推导结果少一个括号,也是因为 keepdims 默认为 False。
四维数组
彩色括号画的人要抓狂了。通用规律:当在某根轴上求和,明晰该轴的元素,再求和。具体说来:
用代码验证一下:
arr = np.arange(1,25).reshape((2,2,2,3))
print(arr)
print( 'The total sum is', arr.sum() )
print( 'The sum on axis0 is', arr.sum(axis=0) )
print( 'The sum on axis1 is', arr.sum(axis=1) )
print( 'The sum on axis2 is', arr.sum(axis=2) )
print( 'The sum on axis3 is', arr.sum(axis=3) )
[[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]]
[[[13 14 15]
[16 17 18]]
[[19 20 21]
[22 23 24]]]]
The total sum is 300
The sum on axis0 is [[[14 16 18]
[20 22 24]]
[[26 28 30]
[32 34 36]]]
The sum on axis1 is [[[ 8 10 12]
[14 16 18]]
[[32 34 36]
[38 40 42]]]
The sum on axis2 is [[[ 5 7 9]
[17 19 21]]
[[29 31 33]
[41 43 45]]]
The sum on axis3 is [[[ 6 15]
[24 33]]
[[42 51]
[60 69]]]
除了 sum 函数,整合函数还包括 min, max, mean, std 和 cumsum,分别是求最小值、最大值、均值、标准差和累加,这些函数对数组里的元素整合方式和 sum 函数相同,就不多讲了。总结来说我们可以对数组
-
所有的元素整合
-
在某个轴 (axis) 上的元素整合
整合函数= {sum, min, max, mean, std, cumsum}
广播机制计算
当对两个形状不同的数组按元素操作时,可能会触发「广播机制」。具体做法,先适当复制元素使得这两个数组形状相同后再按元素操作,两个步骤:
-
广播轴 (broadcast axis):比对两个数组的维度,将形状小的数组的维度 (轴) 补齐
-
复制元素:顺着补齐的轴,将形状小的数组里的元素复制,使得最终形状和另一个数组吻合
在给出「广播机制」需要的严谨规则之前,我们先来看看几个简单例子。
例一:标量和一维数组
arr = np.arange(5)
print(arr)
print(arr + 2)
[0 1 2 3 4]
[2 3 4 5 6]
元素 2 被广播到数组 arr 的所有元素上。
例二:一维数组和二维数组
arr = np.arange(12).reshape((4, 3))
print(arr)
print(arr.mean(axis=0))
print(arr - arr.mean(axis=0))
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
[4.5 5.5 6.5]
[[-4.5 -4.5 -4.5]
[-1.5 -1.5 -1.5]
[ 1.5 1.5 1.5]
[ 4.5 4.5 4.5]]
沿轴 0 的均值的一维数组被广播到数组 arr 的所有的行上。
现在我们来看看「广播机制」的规则:
广播机制的规则
当我们对两个数组操作时,如果它们的形状
-
不相容 (incompatible),广播机制不能进行
-
相容 (compatible),广播机制可以进行
因此,进行广播机制分两步
- 检查两个数组形状是否兼容,即从两个形状元组最后一个元素,来检查
a.它们是否相等
b.是否有一个等于 1
- 一旦它们形状兼容,确定两个数组的最终形状。
例三:维度一样,形状不一样
用个例子来应用以上广播机制规则
a = np.array([[1,2,3]])
b = np.array([[4],[5],[6]])
print( 'The shape of a is', a.shape )
print( 'The shape of b is', b.shape )
The shape of a is (1, 3)
The shape of b is (3, 1)
回顾进行广播机制的两步
-
检查数组 a 和 b 形状是否兼容,从两个形状元组 (1, 3) 和 (3, 1)最后一个元素开始检查,发现它们都满足『有一个等于 1』的条件。
-
因此它们形状兼容,两个数组的最终形状为 (max(1,3), max(3,1)) = (3, 3)
到此,a 和 b 被扩展成 (3, 3) 的数组,让我们看看 a + b 等于多少
c = a + b
print( 'The shape of c is', c.shape )
print( 'a is', a )
print( 'b is', b )
print( 'c = a + b =', c )
The shape of c is (3, 3)
a is [[1 2 3]]
b is [[4]
[5]
[6]]
c = a + b = [[5 6 7]
[6 7 8]
[7 8 9]]
例四:维度不一样
a = np.arange(5)
b = np.array(2)
print( 'The dimension of a is', a.ndim, 'and the shape of a is', a.shape )
print( 'The dimension of b is', b.ndim, 'and the shape of b is', b.shape )
The dimension of a is 1 and the shape of a is (5,)
The dimension of b is 0 and the shape of b is ()
数组 a 和 b 形状分别为 (5,) 和 (),首先我们把缺失的维度用 1 补齐得到 (5,) 和 (1,),再根据广播机制那套流程得到这两个形状是兼容的,而且最终形状为 (5,)。
用代码来看看 a + b 等于多少
c = a + b
print( 'The dimension of c is', c.ndim, 'and the shape of c is', c.shape, '\n' )
print( 'a is', a )
print( 'b is', b )
print( 'c = a + b =', c )
The dimension of c is 1 and the shape of c is (5,)
a is [0 1 2 3 4]
b is 2
c = a + b = [2 3 4 5 6]
现在对广播机制有概念了吧,来趁热打铁搞清楚下面这五个例子,你就完全弄懂它了。
a = np.array( [[[1,2,3], [4,5,6]]] )
b1 = np.array( [[1,1,1], [2,2,2], [3,3,3]] )
b2 = np.arange(3).reshape((1,3))
b3 = np.arange(6).reshape((2,3))
b4 = np.arange(12).reshape((2,2,3))
b5 = np.arange(6).reshape((2,1,3))
print( 'The dimension of a is', a.ndim, 'and the shape of a is', a.shape )
print( 'The dimension of b1 is', b.ndim, 'and the shape of b1 is', b1.shape, '\n')
print( 'The dimension of a is', a.ndim, 'and the shape of a is', a.shape )
print( 'The dimension of b2 is', b.ndim, 'and the shape of b2 is', b2.shape, '\n' )
print( 'The dimension of a is', a.ndim, 'and the shape of a is', a.shape )
print( 'The dimension of b3 is', b.ndim, 'and the shape of b3 is', b3.shape, '\n' )
print( 'The dimension of a is', a.ndim, 'and the shape of a is', a.shape )
print( 'The dimension of b4 is', b.ndim, 'and the shape of b4 is', b4.shape, '\n' )
print( 'The dimension of a is', a.ndim, 'and the shape of a is', a.shape )
print( 'The dimension of b5 is', b.ndim, 'and the shape of b5 is', b5.shape )
The dimension of a is 3 and the shape of a is (1, 2, 3)
The dimension of b1 is 0 and the shape of b1 is (3, 3)
The dimension of a is 3 and the shape of a is (1, 2, 3)
The dimension of b2 is 0 and the shape of b2 is (1, 3)
The dimension of a is 3 and the shape of a is (1, 2, 3)
The dimension of b3 is 0 and the shape of b3 is (2, 3)
The dimension of a is 3 and the shape of a is (1, 2, 3)
The dimension of b4 is 0 and the shape of b4 is (2, 2, 3)
The dimension of a is 3 and the shape of a is (1, 2, 3)
The dimension of b5 is 0 and the shape of b5 is (2, 1, 3)
对于数组 a 和 b1,它们形状是 (1, 2, 3) 和 (3, 3)。元组最后一个都是 3,兼容;倒数第二个是 3 和 2,即不相等,也没有一个是 1,不兼容!a 和 b1 不能进行广播机制。不行就看看下面代码:
c1 = a + b1
print( c1 )
print( c1.shape )
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
in
----> 1 c1 = a + b1
2 print( c1 )
3 print( c1.shape )
ValueError: operands could not be broadcast together with shapes (1,2,3) (3,3)
a 和其他 b2, b3, b4, b5 都可以进行广播机制
c2 = a + b2
print( c2 )
print( c2.shape )
c3 = a + b3
print( c3 )
print( c3.shape )
c4 = a + b4
print( c4 )
print( c4.shape )
c5 = a + b5
print( c5 )
print( c5.shape )
[[[1 3 5]
[4 6 8]]]
(1, 2, 3)
[[[ 1 3 5]
[ 7 9 11]]]
(1, 2, 3)
[[[ 1 3 5]
[ 7 9 11]]
[[ 7 9 11]
[13 15 17]]]
(2, 2, 3)
[[[ 1 3 5]
[ 4 6 8]]
[[ 4 6 8]
[ 7 9 11]]]
(2, 2, 3)
总结
NumPy 终于完结!讨论了的数组创建、数组存载和数组获取、数组变形、数组计算。
数组变形有以下重要操作:
-
改变维度的重塑和打平
-
改变分合的合并和分裂
-
复制本质的重复和拼接
-
其他排序插入删除复制
数组计算有以下重要操作:
-
元素层面:四则运算、函数,比较
-
线性代数:务必弄懂点乘函数 dot()
-
元素整合:务必弄懂轴这个概念!
-
广播机制:太重要了,神经网络无处不在!
学习来源于大佬:原文链接