使用python统计建模和计量经济学工具包Statsmodels进行线性回归

from:   http://www.vkandian.cn/news_keji/topic_2153383/

Statsmodels是Python的统计建模和计量经济学工具包，包括一些描述统计、统计模型估计和推断。

理解什么是线性回归

线性回归也被称为最小二乘法回归（Linear Regression, also called Ordinary Least-Squares (OLS) Regression）。 它的数学模型是这样的：

y = a+ b* x＋e

其中，a被称为常数项或截距、b被称为模型的回归系数或斜率、e为误差项。 a和b是模型的参数

当然，模型的参数只能从样本数据中估计出来：

y'= a' + b'* x

我们的目标是选择合适的参数，让这一线性模型最好地拟合观测值 拟合程度越高，模型越好

那么，接下来的问题就是， 我们如何判断拟合的质量呢？

这一线性模型可以用二维平面上的一条直线来表示，被称为回归线

模型的拟合程度越高，也即意味着样本点围绕回归线越紧密

如何计算样本点与回归线之间的紧密程度呢？

高斯和勒让德找到的方法是：被选择的参数，应该使算出来的回归线与观测值之差的平房和最小。 用函数表示为：

这被称为最小二乘法 最小二乘法的原理是这样的：当预测值和实际值距离的平方和最小时，就选定模型中的两个参数（a和b） 这一模型并不一定反映解释变量和反应变量真实的关系。 但它的计算成本低、、相比复杂模型更容易解释

模型估计出来后，我们要回答的问题是：

1. 我们的模型拟合程度如何？或者说，这个模型对因变量的解释力如何？（R2）

2. 整个模型是否能显著预测因变量的变化？（F检验）

3. 每个自变量是否能显著预测因变量的变化？（t检验）

首先回答第一个问题。 为了评估模型的拟合程度如何，我们必须有一个可以比较的基线模型

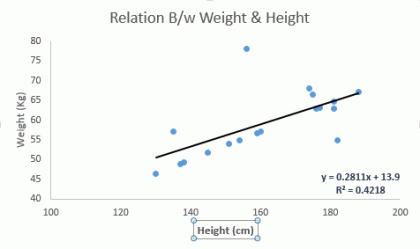
如果让你预测一个人的体重是多少？在没有任何额外信息的情况下，你可能会用平均值来预测，尽管会存在一定误差，但总比瞎猜好

现在，如果你知道他的身高信息，你的预测值肯定与平均值不一样。 额外信息相比平均值更能准确地预测被预测的变量的能力，就代表模型的解释力大小

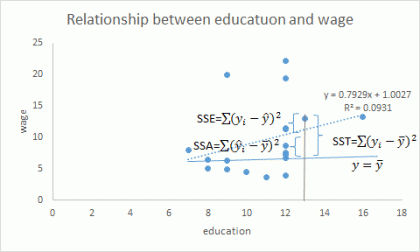
上图中，SSA代表由自变量x引起的y的离差平方和，即回归平方和，代表回归模型的解释力、SSE代表由随机因素引起的y的离差平方和，即剩余平方和，代表回归模型未能解释的部分、SST为总的离差平方和，即我们仅凭y的平均值去估计y时所产生的误差

用模型能够解释的变异除以总的变异就是模型的拟合程度：

R2=SSA/SST=1-SSE

R2（R的平方）也被称为决定系数或判定系数

第二个问题，我们的模型是否显著预测了y的变化？

假设y与x的线性关系不明显，那么SSA相对SSE占有较大的比例的概率则越小。 换句话说，在y与x无线性关系的前提下，SSA相对SSE的占比越高的概率是越小的，这会呈现一定的概率分布。 统计学家告诉我们它满足F分布，就像这样：

如果SSA相对SSE占比较大的情况出现了，比如根据F分布，这个值出现的概率小于5%。那么，我们最好是拒绝y与x线性关系不显著的原始假设，认为二者存在显著的线性关系较为合适。

第三个问题，每个自变量是否能显著预测因变量的变化？换句话说，回归系数是否显著？

回归系数的显著性检验是围绕回归系数的抽样分布（t分布）来进行的，推断过程类似于整个模型的检验过程，不赘言。

实际上，对于只有一个自变量的一元线性模型，模型的显著性检验和回归系数的检验是一致的，但对于多元线性模型来说，二者就不能、、价了

利用statsmodels进行最小二乘回归

＃导入相应模块

In [1]: import numpy as np

In [2]: import pandas as pd

In [3]: import statsmodels.api as sm

＃将数据导入pandas的dataframe对象，第一列（年份）作为行标签

In [4]: df=pd.read_csv('/Users/xiangzhendong/Downloads/vincentarelbundock-Rdatasets-1218370/csv/datasets/longley.csv', index_col=0)

＃查看头部数据

In [5]: df.head()

Out[5]:

      GNP.deflator      GNP  Unemployed  Armed.Forces  Population  Year  \

1947          83.0  234.289       235.6         159.0     107.608  1947

1948          88.5  259.426       232.5         145.6     108.632  1948

1949          88.2  258.054       368.2         161.6     109.773  1949

1950          89.5  284.599       335.1         165.0     110.929  1950

1951          96.2  328.975       209.9         309.9     112.075  1951

      Employed

1947    60.323

1948    61.122

1949    60.171

1950    61.187

1951    63.221

＃设置预测变量和结果变量，用GNP预测Employed

In [6]: y=df.Employed ＃结果变量

In [7]: X=df.GNP ＃预测变量

＃为模型增加常数项，即回归线在y轴上的截距

In [8]: X=sm.add_constant(X) 

＃执行最小二乘回归，X可以是numpy array或pandas dataframe（行数、、于数据点个数，列数为预测变量个数），y可以是一维数组（numpy array）或pandas series

In [10]: est=sm.OLS(y,X)

#使用OLS对象的fit()方法来进行模型拟合

In [11]: est=est.fit()

结果est类成员和成员函数参考：

http://www.statsmodels.org/devel/generated/statsmodels.regression.linear_model.RegressionResults.html

＃查看模型拟合的结果

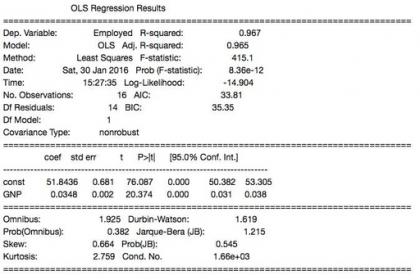
In [12]: est.summary()

Out[12]:

＃查看最终模型的参数

In [13]: est.params

Out[13]:

const    51.843590

GNP       0.034752

dtype: float64

＃选择100个从最小值到最大值平均分布（equally spaced）的数据点

In [14]: X_prime=np.linspace(X.GNP.min(), X.GNP.max(),100)[:,np.newaxis]

In [15]: X_prime=sm.add_constant(X_prime)

＃计算预测值

In [16]: y_hat=est.predict(X_prime)

In [17]: plt.scatter(X.GNP, y, alpha=0.3) ＃画出原始数据

＃分别给x轴和y轴命名

In [18]: plt.xlabel("Gross National Product")

In [19]: plt.ylabel("Total Employment")

In [20]: plt.plot(X_prime[:,1], y_hat, 'r', alpha=0.9) ＃添加回归线，红色

多元线性回归（预测变量不止一个）

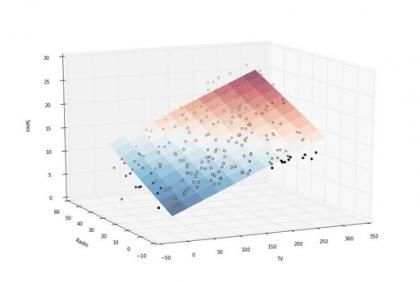
我们用一条直线来描述一元线性模型中预测变量和结果变量的关系，而在多元回归中，我们将用一个多维（p）空间来拟合多个预测变量。 下面表现了两个预测变量的三维图形：商品的销量以及在电视和广播两种不同媒介的广告预算

数学模型是：

Sales = beta_0 + beta_1＊TV + beta_2＊Radio

图中，白色的数据点是平面上的点，黑色的数据点事平面下的点。 平面的颜色是由对应的商品销量的高低决定的，高是红色，低是蓝色

利用statsmodels进行多元线性回归

In [1]: import pandas as pd

In [2]: import numpy as np

In [3]: import statsmodels.api as sm

In [4]: df_adv=pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv',index_col=0)

In [6]: X=df_adv[['TV','Radio']]

In [7]: y=df_adv['Sales']

In [8]: df_adv.head()

Out[8]:

      TV  Radio  Newspaper  Sales

1  230.1   37.8       69.2   22.1

2   44.5   39.3       45.1   10.4

3   17.2   45.9       69.3    9.3

4  151.5   41.3       58.5   18.5

5  180.8   10.8       58.4   12.9

In [9]: X=sm.add_constant(X)

In [10]: est=sm.OLS(y,X).fit()

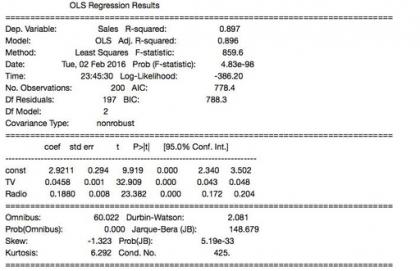
In [11]: est.summary()

Out[11]:

#你也可以使用statsmodels的formula模块来建立多元回归模型

In [12]: import statsmodels.formula.api as smf

In [13]: est=smf.ols(formula='Sales ~ TV + Radio',data=df_adv).fit()

参考资料：

1. DataRobot | Ordinary Least Squares in Python

2. DataRoboe | Multiple Regression using Statsmodels

3. AnalyticsVidhya | 7 Types of Regression Techniques you should know!

4. 维基百科 | 最小二乘法