GLM
原文地址:http://www.cnblogs.com/sumai/p/5240170.html
http://www.cnblogs.com/BYRans/
https://blog.csdn.net/tudaodiaozhale/article/details/80432552
0 准备知识:多项式分布
多项式分布是二项分布的推广。二项分布(也叫伯努利分布)的典型例子是扔硬币,硬币正面朝上概率为p, 重复扔n次硬币,k次为正面的概率即为一个二项分布概率。而多项分布就像扔骰子,有6个面对应6个不同的点数。二项分布时事件X只有2种取值,而多项分布的X有多种取值,多项分布的概率公式为
P ( X 1 = x 1 , ⋯ , X k = x k ) = { n ! x 1 ! , ⋯ , x k ! p x 1 ⋯ p x k , ∑ i = 1 k x i = n 0 , o t h e r w i s e P(X_1=x_1,\cdots,X_k=x_k)= \left\{\begin{array}{ll} \frac{n!}{x_1!,\cdots,x_k!}p^{x_1}\cdots p^{x_k},&\sum\limits_{i=1}^k x_i=n\\ 0,& otherwise \end{array}\right. P(X1=x1,⋯,Xk=xk)=⎩⎨⎧x1!,⋯,xk!n!px1⋯pxk,0,i=1∑kxi=notherwise
下面证明这个式子.
多项式定理:当n是一个正整数时,我们有
(x_1+x_2+\cdots+x_k)^n=\sum\frac{n!}{r_1!r_2!\cdots r_k!}x_1^{r_1}\cdots x_k^{r_k}
其中, r 1 + ⋯ + r k = n , r i ≥ 0 , 1 ≤ i ≤ k . r_1+\cdots+r_k=n,r_i\geq 0,1\leq i \leq k. r1+⋯+rk=n,ri≥0,1≤i≤k.
这个多项式定理的推导如下,将式子左边展开
(x_1+x_2+\cdots+x_k)^n=(x_1+x_2+\cdots+x_k)\cdots(x_1+x_2+\cdots+x_k)
上面的式子是由n个因子相乘得到,而它的展开式可以看做在每个式子里选取某一个xi,总共选取n个xi相乘,所以所有的展开式项都会有
x_1^{r_1}x_2^{r_2}\cdots x_k^{r_k}
这样的公有项,而且 r 1 + ⋯ + r k = n r_1+\cdots+r_k=n r1+⋯+rk=n.
这样的话,我们可以把问题看成在n个式子里,先选取 r 1 r_1 r1个 x 1 x_1 x1,然后选取 r 2 r_2 r2个 x 2 x_2 x2,最后选取 r k r_k rk个 x k x_k xk,然后求有多少种方法。类似把n 个球放到k个不同的盒子里的方法有多少种,我们得到
C_n^{r_1,r_2,\cdots,r_k}=C_n^{r_1}C_{n-r_1}^{r_2}\cdots C_{n-r_1-\cdots-r_{k-1}}^{r_k}=\frac{n!}{r_1!r_2!\cdots r_k!}
所以 x 1 r 1 x 2 r 2 ⋯ x k r k x_1^{r_1}x_2^{r_2}\cdots x_k^{r_k} x1r1x2r2⋯xkrk的系数为 C n r 1 , r 2 , ⋯ , r k C_n^{r_1,r_2,\cdots,r_k} Cnr1,r2,⋯,rk,这样,我们就能得到展开式的通式。举个例子,当k=2时,我们就得到了常见的二项式公式:
(a+b)^n=\sum\limits_{i=0}^n C_n^{i} a^i b^{n-i}.
再来看之前的多项分布的概率公式,假设 X 1 , X 2 , ⋯ , X k X_1,X_2,\cdots,X_k X1,X2,⋯,Xk发生的概率为 p 1 , p 2 , ⋯ , p k p_1,p_2,\cdots,p_k p1,p2,⋯,pk,由于事件之间是相互独立的,可得 p 1 + p 2 + ⋯ + p k = 1 p_1+p_2+\cdots+p_k=1 p1+p2+⋯+pk=1.
我们将式子 p 1 + p 2 + ⋯ + p k = 1 p_1+p_2+\cdots+p_k=1 p1+p2+⋯+pk=1的左边看做一次抽样各种事件发生的概率和,那么 ( p 1 + p 2 + ⋯ + p k ) n = 1 n = 1 (p_1+p_2+\cdots+p_k)^n=1^n=1 (p1+p2+⋯+pk)n=1n=1则是进行了n次抽样所有事件相互组合的对应概率和。把这个多项式展开,它的每一项都对应着一个特殊事件的出现概率。我们把展开式的通项作为 X 1 X_1 X1出现 x 1 x_1 x1次, X 2 X_2 X2出现 x 2 x_2 x2次, ⋯ \cdots ⋯, X k X_k Xk出现 x k x_k xk次的这种事件的出现概率,这样就得到了多项分布的概率公式。
1 指数分布族
1.1 定义
我们在建模的时候,关心的目标变量Y可能服从很多种分布。像线性回归,我们会假设目标变量Y服从正态分布,而逻辑回归,则假设服从伯努利分布。在广义线性模型的理论框架中,则假设目标变量Y则是服从指数分布族,正态分布和伯努利分布都属于指数分布族,因此线性回归和逻辑回归可以看作是广义线性模型的特例。那什么是指数分布族呢?若一个分布的概率密度或者概率分布可以写成这个形式,那么它就属于指数分布族,
p(y,\eta)=b(y)exp(\eta^TT(y)-a(\eta))
其中,η成为分布的自然参数(nature parameter);T(y)是充分统计量(sufficient statistic),通常T(y)=y。 e x p − a ( η ) exp^{-a(\eta)} exp−a(η)是起到归一化作用。当参数 a、b、T 都固定的时候,就定义了一个以η为参数的函数族。
统计中很多熟悉的概率分布都是指数族分布的特定形式,如伯努利分布,高斯分布,多项分布(multionmal), 泊松分布等。下面介绍其中的伯努利分布和高斯分布。
- 伯努利分布
p ( y ; ϕ ) = ϕ y ( 1 − ϕ ) 1 − y p(y;\phi)=\phi^y(1-\phi)^{1-y} p(y;ϕ)=ϕy(1−ϕ)1−y
= e x p [ y l o g ϕ + ( 1 − y ) l o g ( 1 − ϕ ) ] \qquad\quad=exp[ylog\phi+(1-y)log(1-\phi)] =exp[ylogϕ+(1−y)log(1−ϕ)]
= e x p ( y l o g ϕ 1 − ϕ + l o g ( 1 − ϕ ) ] \qquad\quad=exp(ylog\frac{\phi}{1-\phi}+log(1-\phi)] =exp(ylog1−ϕϕ+log(1−ϕ)]
把伯努利分布可以写成指数族分布的形式,则
T ( y ) = y η = l o g ϕ 1 − ϕ a ( η ) = − l o g ( 1 − ϕ ) = l o g ( 1 + e η ) , b ( y ) = 1 \begin{array}{cll} T(y)&=&y \\ \eta&=&log\frac{\phi}{1-\phi} \\ a(\eta)&=&-log(1-\phi)=log(1+e^{\eta}),b(y)=1 \end{array} T(y)ηa(η)===ylog1−ϕϕ−log(1−ϕ)=log(1+eη),b(y)=1.
同时我们可以看到 ϕ = 1 1 + e − η \phi=\frac{1}{1+e^{-\eta}} ϕ=1+e−η1,居然是logistic sigmoid的形式,后面在讨论LR是广义线性模型时,也会用到。
- 高斯分布
高斯分布也可以写为指数族分布的形式如下:
p ( y ; μ ) = 1 2 π e x p ( − 1 2 ( y − μ ) 2 ) p(y;\mu)=\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}(y-\mu)^2) p(y;μ)=2π1exp(−21(y−μ)2)
= 1 2 π e x p ( − 1 2 y 2 ) e x p ( μ y − 1 2 μ 2 ) \qquad\quad=\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}y^2)exp(\mu y-\frac{1}{2}\mu ^2) =2π1exp(−21y2)exp(μy−21μ2).
我们假设方差为1,当然不为1的时候也是可以推导的。上述我们就把高斯分布写为了指数族分布的形式,对应的
η = μ T ( y ) = y a ( η ) = μ 2 / 2 = η 2 / 2 b ( y ) = 1 2 π e x p ( − 1 2 y 2 ) \begin{array}{cll} \eta&=&\mu \\ T(y)&=&y \\ a(\eta)&=&\mu^2/2=\eta^2/2 \\ b(y)&=&\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}y^2) \end{array} ηT(y)a(η)b(y)====μyμ2/2=η2/22π1exp(−21y2)
2 广义线性模型(GLM)
本节将讲述广义线性模型的概念,以及LR,最小二乘为何也属于广义线性模型。
考虑一个分类或回归问题,我们就是想预测某个随机变量yy,yy 是某些特征(feature)xx的函数。为了推导广义线性模式,我们必须做出如下三个假设:
- 1 p ( y ∣ x ; θ ) p(y|x;\theta) p(y∣x;θ)服从指数族分布;
- 2 给了x, 我们的目的是为了预测T(y)的在条件x下的期望。一般情况T(y)=y, 这就意味着我们希望预测h(x)=E[y|x];
- 3 参数η和输入x是线性相关的: η = θ T x \eta=\theta^T x η=θTx.
在这三个假设(也可以理解为一种设计)的前提下,我们可以推导出一系列学习算法,称之为广义线性模型(GLM)。下面我们可以推导出一系列算法,称之为广义线性模型GLM.
2.1 最小二乘法
假设 p ( y ∣ x ; θ ) ∼ N ( μ , σ 2 ) p(y|x;\theta)\sim N(\mu,\sigma^2) p(y∣x;θ)∼N(μ,σ2),则,
h θ = E [ y ∣ x ; θ ] = μ = η = θ T x \begin{array}{cll} h_{\theta}&=&E[y|x;\theta]\\ &=&\mu \\ &=&\eta \\ &=&\theta^T x \end{array} hθ====E[y∣x;θ]μηθTx
第一行因为假设2,第二行因为高斯分布的特点,第三行根据上面高斯分布为指数族分布的推导,第四行因为假设3.
2.2 逻辑回归问题
考虑LR二分类问题, y ∈ 0 , 1 y\in 0,1 y∈0,1,因为是二分类问题,我们很自然的选择 p ( y ∣ x ; θ ) ∼ B e r n o u l l i ( θ ) p(y|x;\theta)\sim Bernoulli(\theta) p(y∣x;θ)∼Bernoulli(θ),即服从伯努利分布。那么
h θ ( x ) = E [ y ∣ x ; θ ] = ϕ = 1 1 + e − ϕ = 1 1 + e − θ T x h_{\theta}(x)=E[y|x;\theta]=\phi=\frac{1}{1+e^{-\phi}}=\frac{1}{1+e^{-\theta^Tx}} hθ(x)=E[y∣x;θ]=ϕ=1+e−ϕ1=1+e−θTx1.
第一行因为假设2,第二行因为伯努利分布的性质,第三行因为伯努利分布为指数族分布时的推导,第四行因为假设3.
所以我们终于知道逻辑回归LR的 p ( y = 1 ∣ x ) = 1 1 + e − θ T x p(y=1|x)=\frac{1}{1+e^{-\theta^Tx}} p(y=1∣x)=1+e−θTx1从何而来了。
2.3 Softmax Regression
Softmax Regression是GLM的另外一个例子。假设预测值 y 有 k 种可能,即 y∈{1,2,…,k}。比如 k=3 时,可以看作是要将一封未知邮件分为垃圾邮件、个人邮件还是工作邮件这三类。
- 步骤一:
假设y服从推广的伯努利分布(多项式分布中n=1的情况),总共有k个类别,用k-1个参数 ϕ 1 , ⋯ , ϕ k − 1 , ϕ k ( ϕ k = 1 − ∑ i = 1 k − 1 ϕ i ) \phi_1,\cdots,\phi_{k-1},\phi_k(\phi_k=1-\sum\limits_{i=1}^{k-1}\phi_i) ϕ1,⋯,ϕk−1,ϕk(ϕk=1−i=1∑k−1ϕi)代表y属于每一类的概率。
接着,我们要把y的分布写成指数分布族的形式。首先,先考虑伯努利分布的表达式为: p ( y ; ϕ ) = ϕ y ( 1 − ϕ ) 1 − y ( y ∈ { 0 , 1 } p(y;\phi)=\phi^y(1-\phi)^{1-y}(y\in \{0,1\} p(y;ϕ)=ϕy(1−ϕ)1−y(y∈{0,1},这是y只有两个分类的情况。现在,我们的y有k个情况,这是我们引入一个示性函数1{.}(1{True} = 1, 1{False} = 0)。
那么这时候y服从分布: p ( y ; ϕ ) = ϕ 1 1 { y = 1 } ϕ 1 1 { y = 2 } ⋯ ϕ 1 1 { y = k } p(y;\phi)=\phi_1^{1\{y=1\}}\phi_1^{1\{y=2\}}\cdots \phi_1^{1\{y=k\}} p(y;ϕ)=ϕ11{y=1}ϕ11{y=2}⋯ϕ11{y=k},然后我们把它写成指数分布族的形式:
$
\begin{array}{lcl}
p(y;\phi)&=&\phi_1{1{y=1}}\phi_1{1{y=2}}\cdots \phi_1^{1{y=k}} \
&=&\phi_1{1{y=1}}\phi_1{1{y=2}}\cdots \phi_1{1-\sum\limits_{i=1}{k-1}1{y=i}}\
&=&exp[1{y=1}log(\phi_1)+\cdots +(1-\sum\limits_{i=1}^{k-1}1{y=i})log(\phi_k)]\
&=&exp[1{y=1}log(\frac{\phi_1}{\phi_k})+\cdots +1{y=k-1}log(\frac{\phi_{k-1}}{\phi_k}+log(\phi_k)] \
&=&b(y)exp(\eta^TT(y)-a(\eta))
\end{array}
$
其中,
η = [ l o g ( ϕ 1 / ϕ k ) l o g ( ϕ 2 / ϕ k ) ⋮ l o g ( ϕ k − 1 / ϕ k ) ] \eta=\begin{bmatrix} log(\phi_1/\phi_k) \\ log(\phi_2/\phi_k) \\ \vdots \\ log(\phi_{k-1}/\phi_k) \end{bmatrix} η=⎣⎢⎢⎢⎡log(ϕ1/ϕk)log(ϕ2/ϕk)⋮log(ϕk−1/ϕk)⎦⎥⎥⎥⎤,
T ( y ) = [ 1 { y = 1 } 1 { y = 2 } ⋮ 1 { y = k − 1 } ] T(y)=\begin{bmatrix} 1\{y=1\}\\1\{y=2\}\\ \vdots \\ 1\{y=k-1\} \end{bmatrix} T(y)=⎣⎢⎢⎢⎡1{y=1}1{y=2}⋮1{y=k−1}⎦⎥⎥⎥⎤,
a ( η ) = − l o g ( ϕ k ) , b ( y ) = 1 a(\eta)=-log(\phi_k),b(y)=1 a(η)=−log(ϕk),b(y)=1.
- 步骤二:
这时候,T(y)是一组 k-1 维的向量,不再是 y,如下所示:
$
T(1)=\begin{bmatrix}1\0\0\ \vdots \ 0\end{bmatrix}
$,
$
T(2)=\begin{bmatrix}0\1\0\ \vdots \ 0\end{bmatrix}
$,
$
T(3)=\begin{bmatrix}0\0\1\ \vdots \ 0\end{bmatrix}
,\cdots,$
$
T(k-1)=\begin{bmatrix}0\0\0\ \vdots \ 1\end{bmatrix}
$,
$
T(k)=\begin{bmatrix}0\0\0\ \vdots \ 0\end{bmatrix}
$.
首先,构造 h θ ( x ) h_{\theta}(x) hθ(x):
h θ ( x ) = E [ T ( y ) ∣ x ; θ ] = E [ 1 { y = 1 } 1 { y = 2 } ⋮ 1 { y = k − 1 } ] = [ ϕ 1 ϕ 2 ⋮ ϕ k − 1 ] h_{\theta}(x)=E[T(y)|x;\theta] =E\begin{bmatrix} 1\{y=1\}\\ 1\{y=2\} \\ \vdots \\ 1\{y=k-1\} \end{bmatrix} =\begin{bmatrix} \phi_1 \\ \phi_2 \\ \vdots \\ \phi_{k-1} \end{bmatrix} hθ(x)=E[T(y)∣x;θ]=E⎣⎢⎢⎢⎡1{y=1}1{y=2}⋮1{y=k−1}⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡ϕ1ϕ2⋮ϕk−1⎦⎥⎥⎥⎤.
其次,我们可以看到:
η i = l o g ϕ i ϕ k \eta_i=log\frac{\phi_i}{\phi_k} ηi=logϕkϕi.
当i=0时上式为零。我们的目的是为了得到参数,于是
e η i = ϕ i ϕ k ⇒ ϕ k e ϕ i = ϕ i ⇒ ϕ k ∑ i = 1 k e η i = ∑ i = 1 k ϕ i = 1 e^{\eta_i}=\frac{\phi_i}{\phi_k}\Rightarrow \phi_k e^{\phi_i}= \phi_i\Rightarrow \phi_k\sum\limits_{i=1}^k e^{\eta_i}=\sum\limits_{i=1}^k \phi_i =1 eηi=ϕkϕi⇒ϕkeϕi=ϕi⇒ϕki=1∑keηi=i=1∑kϕi=1.
最后我们终于得到:
\phi_i=\frac{e^{\eta_i}}{\sum\limits_{j=1}^k e^{\eta_j}}.
上式将η映射到φ,此函数称为softmax函数.
- 步骤三:
又根据线性假设,对于每个η有 η i = θ i T X ( i = 1 , 2 , ⋯ , k − 1 ) \eta_i=\theta_i^TX(i=1,2,\cdots,k-1) ηi=θiTX(i=1,2,⋯,k−1),同时令 η k = 0 \eta_k=0 ηk=0,对求和式没有影响,那么有
\begin{array}{lcl}
p(y=i|x;\theta)&=&\phi_i \\
&=&\frac{e^{\eta_i}}{\sum_{j=1}^k e^{\eta_j}}\\
&=&\frac{e^{\theta_i^T x}}{\sum_{j=1}^k e^{\theta_j^T x}}
\end{array}
综上所述,得到的预测函数h为:
\begin{array}{lcl}
h_{\theta}(x)&=&E[T(y)|x;\theta]
=E\begin{bmatrix}
1\{y=1\}\\ 1\{y=2\} \\ \vdots \\ 1\{y=k-1\}
\end{bmatrix}
=\begin{bmatrix}
\phi_1 \\ \phi_2 \\ \vdots \\ \phi_{k-1}
\end{bmatrix} \\
&=&\begin{bmatrix}
\frac{exp(\theta_1^Tx)}{\sum\limits_{j=1}^k exp(\theta_j^T x)} \\
\frac{exp(\theta_2^Tx)}{\sum\limits_{j=1}^k exp(\theta_j^T x)} \\
\vdots \\
\frac{exp(\theta_{k-1}^Tx)}{\sum\limits_{j=1}^k exp(\theta_j^T x)}
\end{bmatrix}
\end{array}
那么就建立了假设函数,最后就获得了最大似然估计:
\begin{array}{lcl}
\ell(\theta)&=&\sum\limits_{i=1}^m logp(y^{(i)}|x^{(i)};\theta)\\
&=&\sum\limits_{i=1}^m log\prod\limits_{l=1}^k (\frac{e^{\theta_l^Tx^{(i)}}}{\sum_{j=1}^k e^{\theta_j^Tx^{(i)}}})^{1\{y^{(i)}=l\}}
\end{array}
对该式子可以使用梯度下降算法或者牛顿方法求得参数θ后,使用假设函数h对新的样例进行预测,即可完成多类分类任务。对于互斥的多分类问题,这种模型比较合适,而对于非互斥的多分类问题,构建k个one-vs-all逻辑回归模型更为合适。
2.4 Softmax回归 VS k个二元分类器
如果你在开发一个音乐分类的应用,需要对k种类型的音乐进行识别,那么是选择使用softmax分类器呢,还是使用logistic回归算法建立 k个独立的二元分类器呢?
这一选择取决于你的类别之间是否互斥,例如,如果你有四个类别的音乐,分别为:古典音乐、乡村音乐、摇滚乐和爵士乐,那么你可以假设每个训练样本只会被打上一个标签(即:一首歌只能属于这四种音乐类型的其中一种),此时你应该使用类别数 k = 4 的softmax回归。(如果在你的数据集中,有的歌曲不属于以上四类的其中任何一类,那么你可以添加一个“其他类”,并将类别数 k 设为5。)
如果你的四个类别如下:人声音乐、舞曲、影视原声、流行歌曲,那么这些类别之间并不是互斥的。例如:一首歌曲可以来源于影视原声,同时也包含人声 。这种情况下,使用4个二分类的logistic回归分类器更为合适。这样,对于每个新的音乐作品 ,我们的算法可以分别判断它是否属于各个类别。
3 Softmax回归 Python实现
现实中常常会遇到需要多分类的问题,比如手写体识别,你需要识别手写的数字是几(0~9),比如文本生成,你需要知道生成的是哪个字,都需要进行多分类。那么我们最常用的多分类函数就是softmax了。接下来本文将会实现一个softmax来进行手写体识别。
3.1 数据集
本次的数据集分为训练集:文件名为"trainingDigits"和测试集:文件名为"testDigits",每个文件夹里面有txt文件若干,比如’0_83.txt’文件名前部分是标签,后部分是编号,这个可以不用管。用记事本打开文件可以看到,里面是一幅由32X32的0、1数字组成的矩阵。
可以依稀看出是0的手写体,其它类似。
def loadData(self, dir): #给出文件目录,读取数据
digits = list() #数据集(数据)
labels = list() #标签
if os.path.exists(dir): #判断目录是否存在
files = os.listdir(dir) #获取目录下的所有文件名
for file in files: #遍历所有文件
labels.append(file.split('_')[0]) #按照文件名规则,文件名第一位是标签
with open(dir + '\\' + file) as f: #通过“目录+文件名”,获取文件内容
digit = list()
for line in f: #遍历文件每一行
digit.extend(map(int, list(line.replace('\n', '')))) #遍历每行时,把数字通过extend的方法扩展
digits.append(digit) #将数据扩展进去
digits = np.array(digits) #数据集
labels = list(map(int, labels)) #标签
labels = np.array(labels).reshape((-1, 1)) #将标签重构成(N, 1)的大小
return digits, labels
这里由loadData函数实现了对文件夹的读取,并返回数据集和标签。
3.2 算法实现
3.2.1 代价函数
之前的机器学习中,总是将类别分成两类,比如逻辑斯谛回归中,将>=0.5的概率分成正类,<0.5的概率分成负类。如果是要分成多类,那可以将逻辑斯谛回归进行一个推广,比如要分成10类,可以用一个数组表示,就是[0.11, 0.13, 0.06, 0.07, 0.03, 0.15, 0.3, 0.08, 0.03, 0.04]来表示每一个类别的概率,其中0.3概率最大,则有很大可能是这个类别。逻辑斯谛回归用的sigmoid函数,而多分类用的是softmax函数,可以表示成如下形式
p(y=i|x;\theta)=\frac{exp(\theta_i^T x)}{\sum\limits_{j=1}^k exp(\theta_j^T x)}
对应代码,这段代码会返回一个10X1的一个数组(因为我们这次的手写体识别只有10类,从0~9):
def softmax(self, X): #softmax函数
return np.exp(X) / np.sum(np.exp(X))
类似逻辑斯谛回归,其目标函数是对数似然估计:
\begin{array}{lcl}
\ell(\theta)&=&\sum\limits_{i=1}^m logp(y^{(i)}|x^{(i)};\theta)\\
&=&\sum\limits_{i=1}^m log\prod\limits_{l=1}^k (\frac{e^{\theta_l^Tx^{(i)}}}{\sum_{j=1}^k e^{\theta_j^Tx^{(i)}}})^{1\{y^{(i)}=l\}} \\
&=&\sum\limits_{i=1}^m\sum\limits_{l=1}^k 1\{y^{(i)}=l\}log\frac{e^{\theta_l^T x^{(i)}}}{\sum\limits_{j=1}^k e^{\theta_j^T x^{(i)}}}
\end{array}
值得注意的是,上述公式是logistic回归代价函数的推广。logistic回归代价函数可以改为:
ℓ ( θ ) = ∑ i = 1 m y ( i ) l o g π ( z ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − π ( z ( i ) ) ) = ∑ i = 1 m ∑ l = 0 k 1 { y ( i ) = l } l o g p ( y ( i ) = l ∣ x ( i ) ; θ ) \begin{array}{lcl}\ell(\theta)&=&\sum\limits_{i=1}^m y^{(i)}log\pi(z^{(i)})+(1-y^{(i)})log(1-\pi(z^{(i)}))\\ &=&\sum\limits_{i=1}^m\sum\limits_{l=0}^k 1\{y^{(i)}=l\}logp(y^{(i)}=l|x^{(i)};\theta) \end{array} ℓ(θ)==i=1∑my(i)logπ(z(i))+(1−y(i))log(1−π(z(i)))i=1∑ml=0∑k1{y(i)=l}logp(y(i)=l∣x(i);θ)
可以看到,Softmax代价函数与logistic 代价函数在形式上非常类似,只是在Softmax损失函数中对类标记的 \textstyle k 个可能值进行了累加。注意在Softmax回归中将 \textstyle x 分类为类别 \textstyle j 的概率为:
p(y^{(i)}=l|x^{(i)};\theta)=\frac{e^{\theta_l^T x^{(i)}}}{\sum\limits_{j=1}^k e^{\theta_j^T x^{(i)}}}
对于 \textstyle J(\theta) 的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,我们得到梯度公式如下:
\nabla_{\theta_j}J(\theta)=\sum\limits_{i=1}^m[x^{(i)}(1\{y^{(i)}=j\}-p(y^{(i)}=j|x^{(i)};\theta))]
让我们来回顾一下符号" ∇ θ j \nabla_{\theta_j} ∇θj"的含义. ∇ θ j J ( θ ) \nabla_{\theta_j}J(\theta) ∇θjJ(θ)本身是一个向量,它的第 \textstyle l 个元素 ∂ J ( θ ) ∂ θ j t \frac{\partial J(\theta)}{\partial \theta_{jt}} ∂θjt∂J(θ)是 J ( θ ) J(\theta) J(θ)对 θ j \theta_j θj 的第 ℓ \ell ℓ个分量的偏导数。
有了上面的偏导数公式以后,我们就可以将它代入到梯度下降法等算法中,来最小化 J ( θ ) J(\theta) J(θ). 例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新: θ j : = θ j − α ∇ θ j J ( θ ) ( j = 1 , ⋯ , k ) . ) \theta_j:=\theta_j-\alpha \nabla_{\theta_j}J(\theta)(j=1,\cdots,k).) θj:=θj−α∇θjJ(θ)(j=1,⋯,k).).
当实现 softmax 回归算法时, 我们通常会使用上述代价函数的一个改进版本。具体来说,就是和权重衰减(weight decay)一起使用。我们接下来介绍使用它的动机和细节。
3.2.2 Softmax回归模型参数化的特点
Softmax 回归有一个不寻常的特点:它有一个“冗余”的参数集。为了便于阐述这一特点,假设我们从参数向量 θ j \theta_j θj中减去了向量 ψ \psi ψ,这时,每一个 θ j \theta_j θj都变成了 θ j − ψ ( j = 1 , ⋯ , k ) ) \theta_j-\psi(j=1,\cdots,k)) θj−ψ(j=1,⋯,k)).此时假设函数变成了以下的式子:
\begin{array}{lcl}
p(y^{(i)}=j|x^{(i)};\theta)&=&\frac{e^{(\theta_j-\psi)^T x^{(i)}}}{\sum\limits_{l=1}^k e^{(\theta_l-\psi)^Tx^{(i)}}}\\
&=&\frac{e^{\theta_j^Tx^{(i)}}e^{-\psi^Tx^{(i)}}}{\sum\limits_{l=1}^k e^{\theta_l^Tx^{(i)}}e^{-\psi^T x^{(i)}}}\\
&=&\frac{e^{\theta_j^Tx^{(i)}}}{\sum\limits_{l=1}^ke^{\theta_l^Tx^{(i)}}}
\end{array}
换句话说,从 θ j \theta_j θj中减去 ψ \psi ψ完全不影响假设函数的预测结果!这表明前面的 softmax 回归模型中存在冗余的参数。更正式一点来说, Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数 π ( z ) \pi(z) π(z).
进一步而言,如果参数 ( θ 1 , θ 2 , ⋯ , θ k ) (\theta_1,\theta_2,\cdots,\theta_k) (θ1,θ2,⋯,θk)是代价函数 ( θ ) (\theta) (θ)的极小值点,那么 ( θ 1 − ψ , θ 2 − ψ , ⋯ , θ k − ψ ) (\theta_1-\psi,\theta_2-\psi,\cdots,\theta_k-\psi) (θ1−ψ,θ2−ψ,⋯,θk−ψ)同样也是它的极小值点,其中 ψ \psi ψ 可以为任意向量。因此使 J ( θ ) J(\theta) J(θ)最小化的解不是唯一的。(有趣的是,由于 J ( θ ) J(\theta) J(θ)仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题).
注意,当 ψ = θ 1 \psi=\theta_1 ψ=θ1时,我们总是可以将 θ 1 \theta_1 θ1替换为 θ 1 − ψ ) = 0 ⃗ \theta_1-\psi)=\vec{0} θ1−ψ)=0(即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量 θ 1 \theta_1 θ1 (或者其他 θ j \theta_j θj 中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的 k × ( n + 1 ) k\times (n+1) k×(n+1)个参数 ( θ 1 , θ 2 , ⋯ , θ k ) (\theta_1,\theta_2,\cdots,\theta_k) (θ1,θ2,⋯,θk)(其中 θ j ∈ R n + 1 \theta_j\in R^{n+1} θj∈Rn+1),,我们可以令 θ 1 = 0 ⃗ \theta_1=\vec{0} θ1=0,只优化剩余的 ( k − 1 ) × ( n + 1 ) (k-1)\times(n+1) (k−1)×(n+1) 个参数,这样算法依然能够正常工作。
在实际应用中,为了使算法实现更简单清楚,往往保留所有参数 ( θ 1 , θ 2 , ⋯ , θ k ) (\theta_1,\theta_2,\cdots,\theta_k) (θ1,θ2,⋯,θk),而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
3.3.3 权重衰减
我们通过添加一个权重衰减项 λ 2 ∑ i = 1 k ∑ j = 0 n θ i j 2 \frac{\lambda}{2}\sum\limits_{i=1}^k\sum\limits_{j=0}^n \theta_{ij}^2 2λi=1∑kj=0∑nθij2来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
J(\theta)=\sum\limits_{i=1}^m\sum\limits_{j=1}^k [1\{y_{(i)}=j\}log\frac{e^{\theta_j^Tx^{(i)}}}{\sum\limits_{l=1}^k e^{\theta_l^Tx^{(i)}}}]+\frac{\lambda}{2}\sum\limits_{i=1}^k\sum\limits_{j=0}^n \theta_{ij}^2
有了这个权重衰减项以后( λ > 0 \lambda > 0 λ>0),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为 J ( θ ) J(\theta) J(θ)是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
为了使用优化算法,我们需要求得这个新函数 J ( θ ) J(\theta) J(θ)的导数,如下:
\nabla_{\theta_j}J(\theta)=\sum\limits_{i=1}^m[x^{(i)}(1\{y^{(i)}=j\}-p(y^{(i)}=j|x^{(i)};\theta))]+\lambda\theta_j,
通过最小化 J ( θ ) J(\theta) J(θ),我们就能实现一个可用的softmax 回归模型。
3.3.4 计算softmax和数值稳定性
对于一个给定的向量,使用Python来计算softmax的简单方法是:
def softmax(x):
"""Compute the softmax of vector x."""
exps = np.exp(x)
return exps / np.sum(exps)
比如:
In [146]: softmax([1, 2, 3])
Out[146]: array([ 0.09003057, 0.24472847, 0.66524096])
然而当我们使用该函数计算较大的值时(或者大的负数时),会出现一个问题:
In [148]: softmax([1000, 2000, 3000])
Out[148]: array([ nan, nan, nan])
Numpy使用的浮点数的数值范围是有限的。对于float64,最大可表示数字的大小为1030810308。
softmax函数中的求幂运算可以轻松超过这个数字,即使是相当适中的输入。避免这个问题的一个好方法是通过规范输入使其不要太大或者太小,通过观察我们可以使用任意的常量C,如下所示:
S j = e z j ∑ k = 1 n e z k = C e z j ∑ k = 1 n C e z k , \qquad S_j=\frac{e^{z_j}}{\sum_{k=1}^ne^{z_k}}=\frac{Ce^{z_j}}{\sum_{k=1}^nCe^{z_k}}, Sj=∑k=1nezkezj=∑k=1nCezkCezj,
然后将这个变量转换到指数上:
S j = e z j + log ( C ) ∑ k = 1 n e z k + log ( C ) , \qquad S_j=\frac{e^{z_j+\log(C)}}{\sum_{k=1}^ne^{z_k+\log(C)}}, Sj=∑k=1nezk+log(C)ezj+log(C),
因为C是一个随机的常量,所以我们可以写为:
S j = e z j + D ∑ k = 1 n e z k + D , \qquad S_j=\frac{e^{z_j+D}}{\sum_{k=1}^ne^{z_k+D}}, Sj=∑k=1nezk+Dezj+D,
D也是一个任意常量。对任意D,这个公式等价于前面的式子,这让我们能够更好的进行计算。对于D,一个比较好的选择是所有输入的最大值的负数:
D = − m a x ( z 1 , z 2 , ⋯ , z n ) D=-max(z_1,z_2,\cdots,z_n) D=−max(z1,z2,⋯,zn)
假定输入本身彼此相差不大,这会使输入转换到接近于0的范围。最重要的是,它将所有的输入转换为负数(除最大值外,最大值变为0)。很大的负指数结果会趋于0而不是无穷,这就让我们很好的避免了出现NaN的结果。
def stablesoftmax(x):
"""Compute the softmax of vector x in a numerically
stable way."""
shiftx = x - np.max(x)
exps = np.exp(shiftx)
return exps / np.sum(exps)
现在我们有:
In [150]: stablesoftmax([1000, 2000, 3000])
Out[150]: array([ 0., 0., 1.])
请注意,这仍然是不完美的,因为数学上softmax永远不会真的产生零,但这比NaN好得多,且由于输入之间的距离非常大,所以无论如何都会得到非常接近于零的结果。
3.3.5 python实现
实现1
import numpy as np
import math
from matplotlib import pyplot as plt
from sklearn import datasets
#计算假设的“相对概率”分布,注意防止指数运算数据溢出 dataset: m*(n+1) theta: k*(n+1) m:样本数 n:特征数 k:标签类别数
def Hypothesis(theta,dataset):
score=np.dot(theta,dataset.T)
a=np.max(score,axis=0)
exp_score=np.exp(score-a)
sum_score=np.sum(exp_score,axis=0)
relative_probability=exp_score/sum_score
return relative_probability
#计算损失函数
#theta为参数矩阵k*(n+1)
def Cost_function(theta,dataset,labels,lamda):
m,n=dataset.shape
new_code=One_hot_encode(labels)
log_probability = np.log(Hypothesis(theta,dataset))
cost = -1/m * np.sum(np.multiply(log_probability,new_code)) + lamda * np.sum(theta*theta)/2
return cost
#对标签进行独热编码
#new_code为 k*m k为标签数 m为样本数
def One_hot_encode(labels):
m=len(labels)
k=len(np.unique(labels))
new_code=np.zeros((k,m))
for i in range(m):
new_code[labels[i],i]=1
return new_code
#使用Batch Gradient Descent优化损失函数
#迭代终止条件: 1:达到最大迭代次数 2:前后两次梯度变化小于一个极小值 3:迭代前后损失函数值变化极小
#dataset为原始数据集:m*n labels:标签 lamda:正则项系数 learning_rate:学习率 max_iter:最大迭代次数
#eps1:损失函数变化量的阈值 eps2:梯度变化量阈值
def SoftmaxRegression(dataset,labels,lamda,learning_rate,max_iter,eps1,eps2,EPS):
loss_record=[]
m,n = dataset.shape
k = len(np.unique(labels))
new_code = One_hot_encode(labels)
iter = 0
new_cost = 0
cost = 0
dataset=np.column_stack((dataset,np.ones(m)))
theta = np.random.random((k,n+1))
gradient = np.zeros(n)
while iter < max_iter:
new_theta = theta.copy()
temp = new_code - Hypothesis(new_theta,dataset)
for j in range(k):
sum = np.zeros(n+1)
for i in range(m):
a=dataset[i,:]
sum += a * temp[j,i]
j_gradient=-1/m * sum + lamda * new_theta[j,:] #计算属于第j类相对概率的梯度向量
new_theta[j,:] = new_theta[j,:] - learning_rate * j_gradient
iter += 1
#print("第"+str(iter)+"轮迭代的参数:")
new_cost = Cost_function(new_theta,dataset,labels,lamda)
loss_record.append(new_cost)
print("损失函数变化量:" + str(abs(new_cost-cost)))
if abs(new_cost-cost) < eps1:
break
theta = new_theta
cost=new_cost
return theta,loss_record
def Classification(theta,dataset):
X=dataset.copy()
X=np.column_stack((X,np.ones(X.shape[0])))
relative_probability=Hypothesis(theta,X)
return np.argmax(relative_probability,axis=0)
测试:
iris= datasets.load_iris()
X=iris.data
y = iris.target
target_names = iris.target_names
theta,loss_record=SoftmaxRegression(dataset=X,labels=y,lamda=0.1,learning_rate=1e-2,max_iter=500000,eps1=1e-6,eps2=1e-4,EPS=1e-6)
predict=Classification(theta,X)
(predict==y).astype(np.int).mean() #训练集上精度
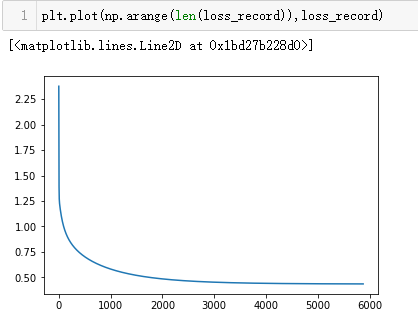
结果为96%,损失函数迭代曲线如下:
实现2
简单实现代码如下:
import numpy as np
import os
class Softmax:
def loadData(self, dir): #给出文件目录,读取数据
digits = list() #数据集(数据)
labels = list() #标签
if os.path.exists(dir): #判断目录是否存在
files = os.listdir(dir) #获取目录下的所有文件名
for file in files: #遍历所有文件
labels.append(file.split('_')[0]) #按照文件名规则,文件名第一位是标签
with open(dir + '\\' + file) as f: #通过“目录+文件名”,获取文件内容
digit = list()
for line in f: #遍历文件每一行
digit.extend(map(int, list(line.replace('\n', '')))) #遍历每行时,把数字通过extend的方法扩展
digits.append(digit) #将数据扩展进去
digits = np.array(digits) #数据集
labels = list(map(int, labels)) #标签
labels = np.array(labels).reshape((-1, 1)) #将标签重构成(N, 1)的大小
return digits, labels
def softmax(self, X): #softmax函数
return np.exp(X) / np.sum(np.exp(X))
def train(self, digits, labels, maxIter = 1000, alpha = 0.1):
self.weights = np.random.uniform(0, 1, (3,4))
for iter in range(maxIter):
for i in range(len(digits)):
x = digits[i].reshape(-1, 1)
y = np.zeros((3, 1))
y[labels[i]] = 1
y_ = self.softmax(np.dot(self.weights, x))
self.weights -= alpha * (np.dot((y_ - y), x.T))
return self.weights
def predict(self, digit): #预测函数
return np.argmax(np.dot(self.weights, digit)) #返回softmax中概率最大的值
if __name__ == '__main__':
softmax = Softmax()
#trainDigits, trainLabels = softmax.loadData('files/softmax/trainingDigits')
#testDigits, testLabels = softmax.loadData('files/softmax/testDigits')
#softmax.train(trainDigits, trainLabels, maxIter=100) #训练
iris= datasets.load_iris()
X=iris.data
y = iris.target
softmax.train(X, y, maxIter=6000) #训练
accuracy = 0
N = len(X) #总共多少测试样本
for i in range(N):
digit = X[i] #每个测试样本
label = y[i] #每个测试标签
predict = softmax.predict(digit) #测试结果
if (predict == label):
accuracy += 1
#print("predict:%d, actual:%d"% (predict, label))
print("accuracy:%.1f%%" %(accuracy / N * 100))
结果为:96%.
备注:Softmax回归与Logistic 回归的关系
当类别数 \textstyle k = 2 时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当 \textstyle k = 2 时,softmax 回归的假设函数为:
\pi(z)=\frac{1}{e^{\theta_1^Tx}+e^{\theta_2^Tx^{(i)}}}
\begin{bmatrix}
e^{\theta_1^Tx}\\e^{\theta_2^Tx}
\end{bmatrix}
利用softmax回归参数冗余的特点,我们令 ψ = θ 1 \psi=\theta_1 ψ=θ1,并且从两个参数向量中都减去向量 θ 1 \theta_1 θ1,得到:
\begin{array}{lcl}
\pi(z)&=&\frac{1}{e^{\vec{0}^T x}+e^{(\theta_2-\theta_1)^Tx^{(i)}}}
\begin{bmatrix}
e^{\vec{0}^T x}\\ e^{(\theta_2-\theta_1)^T x}
\end{bmatrix}\\
&=&\begin{bmatrix}
\frac{1}{1+e^{(\theta_2-\theta_1)^Tx^{(i)}}} \\
\frac{e^{(\theta_2-\theta_1)^T x}}{1+e^{(\theta_2-\theta_1)^Tx^{(i)}}}
\end{bmatrix}\\
&=&\begin{bmatrix}
\frac{1}{1+e^{(\theta_2-\theta_1)^Tx^{(i)}}}\\
1-\frac{1}{1+e^{(\theta_2-\theta_1)^Tx^{(i)}}}
\end{bmatrix}
\end{array}
因此,用 θ ′ \theta' θ′来表示 θ 2 − θ 1 \theta_2-\theta_1 θ2−θ1,我们就会发现 softmax 回归器预测其中一个类别的概率为 1 1 + e ( θ 2 − θ 1 ) T x ( i ) \frac{1}{1+e^{(\theta_2-\theta_1)^Tx^{(i)}}} 1+e(θ2−θ1)Tx(i)1,另一个类别概率的为 1 − 1 1 + e ( θ 2 − θ 1 ) T x ( i ) 1-\frac{1}{1+e^{(\theta_2-\theta_1)^Tx^{(i)}}} 1−1+e(θ2−θ1)Tx(i)1,这与 logistic回归是一致的。
注:有点书上记 π ( z ) : = h θ ( x ) \pi(z):=h_{\theta}(x) π(z):=hθ(x),其中 z = θ T x = θ 1 T x 1 + θ 2 T x 2 + ⋯ + θ k T x k z=\theta^T x=\theta_1^T x_1+\theta_2^T x_2+\cdots+\theta_k^T x_k z=θTx=θ1Tx1+θ2Tx2+⋯+θkTxk,还有的将z记为 z = w 0 + w 1 x 1 + w 2 + x 2 + ⋯ + w k − 1 x k − 1 . z=w_0+w_1x_1+w_2+x_2+\cdots+w_{k-1}x_{k-1}. z=w0+w1x1+w2+x2+⋯+wk−1xk−1.