二叉树中两个节点的最近公共祖先节点
题目:求二叉树中两个节点的最近公共祖先节点
一、该二叉树为搜索二叉树
搜索二叉树的特点:
任意一个节点的左子树的所有节点值都比该节点的值小,其右子树的所有节点值都比该节点的值大。
解决该问题方法:
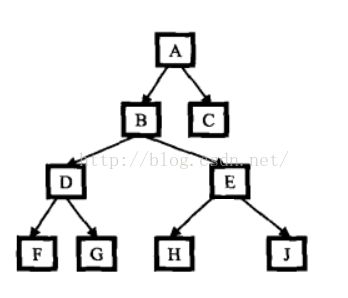
从树的根节点开始和两个节点作比较,如果当前节点的值比两个节点的值都大,则这两个节点的最近公共祖先节点一定在该节点的左子树中,则下一步遍历当前节点的左子树;
如果当前节点的值比两个节点的值都小,则这两个节点的最近公共祖先节点一定在该节点的右子树中,下一步遍历当前节点的右子树;这样直到找到第一个值是两个输入节点之间的值的节点,该节点就是两个节点的最近公共祖先节点。
如图:
二、该二叉树为一般二叉树,有二叉树节点中包含指向父节点的指针
struct BinaryNode
{
BinaryNode* _left;
BinaryNode* _right;
BinaryNode* _parent;
int _value;
BinaryNode(const int& value)
:_value(value)
, _left(NULL)
, _right(NULL)
, _parent(NULL)
{}
};方法一:
首先给出node1的父节点node1->_parent,然后将node1的所有父节点依次和node2->parent作比较,如果发现两个节点相等,则该节点就是最近公共祖先,直接将其返回。如果没找到相等节点,则将node2的所有父节点依次和node1->_parent->_parent作比较......直到node1->_parent==NULL。
代码如下:
BinaryNode * GetLastCommonAncestor(BinaryNode * root, BinaryNode * node1, BinaryNode * node2)
{
BinaryNode * temp;
while (node1 != NULL)
{
node1 = node1->_parent;
temp = node2;
while (temp != NULL)
{
if (node1 == temp->_parent)
return node1;
temp = temp->_parent;
}
}
}该算法时间复杂度为O(n^2),可用另一种O(n)的算法
方法二:
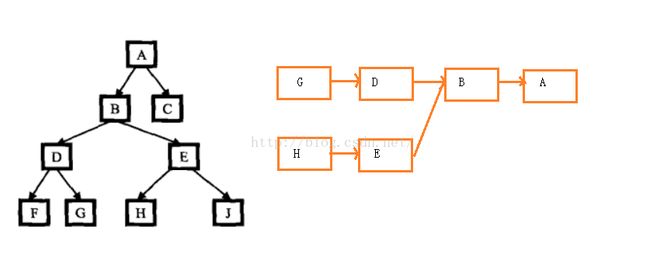
给定的两个节点都含有父节点,因此,可将这两个节点看做是两个链表的头结点,将求两个节点的最近公共祖先节点转化为求两链表的交点,这两个链表的尾节点都是根节点。
如图:
若查找节点G, H的最近公共祖先节点可转化为如图所示的两个链表的交点,可知两节点最近公共祖先节点为B。
代码如下:
int Hight(BinaryNode* root, BinaryNode* node)
{
int len = 0;
for (; node != NULL; node = node->_parent)
len++;
return len;
}BinaryNode* GetLastCommonAncestor(BinaryNode* root, BinaryNode* node1, BinaryNode* node2)
{
if (root == NULL || node1 == NULL || node2==NULL)
return NULL;
int len1 = Hight(root,node1);
int len2 = Hight(root,node2);
for (; len1 > len2; len1--)
node1 = node1->_parent;
for (; len2 > len1; len2--)
node2 = node2->_parent;
while (node1 && node2 && node1 != node2)
{
node1 = node1->_parent;
node2 = node2->_parent;
}
if (node1 == node2)
return node1;
else
return NULL;
}三、该二叉树为一般二叉树,有二叉树节点中没有指向父节点的指针
方法一:1) 找到从根到node1的路径,并存储在一个向量或数组中。
2)找到从根到node2的路径,并存储在一个向量或数组中。
3) 遍历这两条路径,直到遇到一个不同的节点,则前面的那个即为最低公共祖先.
如图,若查找节点G, H的最近公共祖先节点可转化为如图所示的两个数组中的最后一个相同的节点,可知两节点最近公共祖先节点为B。
方法二:
上面的方法虽然是O(n),但是操作依然繁琐,并且需要额外的空间来存储路径。
从根节点开始遍历,如果node1和node2中的任一个和root匹配,那么root就是最低公共祖先。 如果都不匹配,则分别递归左、右子树,如果有一个 节点出现在左子树,并且另一个节点出现在右子树,则root就是最低公共祖先. 如果两个节点都出现在左子树,则说明最低公共祖先在左子树中,否则在右子树。
若求G, H节点的最近公共祖先节点,在B的左子书中找到G, B的右子树中返回H,得到G,H的最低公共祖先B。
代码如下:
BinaryNode* GetLastCommonAncestor(BinaryNode* root, BinaryNode* node1, BinaryNode* node2)
{
if (root == NULL || node1 == NULL || node2 == NULL)
return NULL;
if (node1 == root || node2 == root)
return root;
BinaryNode* cur = NULL;
BinaryNode* left_lca = GetLastCommonAncestor(root->_left, node1, node2);
BinaryNode* right_lca = GetLastCommonAncestor(root->_right, node1, node2);
if (left_lca && right_lca)
return root;
if (left_lca == NULL)
return right_lca;
else
return left_lca;
}该函数当一个节点是另一个节点的祖先时,返回的是离根节点最近的那个节点,要想返回最近公共祖先节点需进行判断两节点是否有祖孙关系,参考代码如下:
简要说明:若两节点为F,D,则判断出B的左子树中的D节点后,继续判断判断节点D的左右子树中是否含有节点F,若有,则返回B,若没有则继续判断右子树中的另一个节点。
参考代码如下:
BinaryNode* GetLastCommonAncestor(BinaryNode* root, BinaryNode* node1, BinaryNode* node2)
{
if (root == NULL || node1 == NULL || node2 == NULL)
return NULL;
if (node1 == root || node2 == root)
return root;
BinaryNode* cur = NULL;
BinaryNode* left_lca = GetLastCommonAncestor(root->_left,node1,node2);
if (NULL != left_lca)
{
cur = GetLastCommonAncestor(left_lca->_left, node1, node2);
if (cur ==NULL)
cur = GetLastCommonAncestor(left_lca->_right, node1, node2);
if ((cur == node1) && (left_lca == node2) || (cur == node2) && (left_lca == node1))
return root;
}
BinaryNode* right_lca = GetLastCommonAncestor(root->_right, node1, node2);
if (NULL != right_lca)
{
cur = GetLastCommonAncestor(right_lca->_left, node1, node2);
if (cur == NULL)
cur = GetLastCommonAncestor(right_lca->_right, node1, node2);
if ((cur == node1) && (left_lca == node2) || (cur == node2) && (left_lca == node1))
return root;
}
if (left_lca && right_lca)
return root;
if (left_lca == NULL)
return right_lca;
else
return left_lca;
}测试用例:
void Test()
{
BinaryNode* root = new BinaryNode(1);
BinaryNode* cur = root;
queue q;
BinaryNode* top = NULL;
q.push(root);
for (int i = 2; i <= 7; i++)
{
if (!q.empty())
{
top = q.front();
if (cur == top->_left)
{
cur = new BinaryNode(i);
top->_right = cur;
cur->_parent = top;
q.pop();
}
else
{
cur = new BinaryNode(i);
top->_left = cur;
cur->_parent = top;
}
q.push(cur);
}
}
BinaryNode* node1 = root->_left->_left;
BinaryNode* node2 = root->_left->_right;
BinaryNode* ancestor = GetLastCommonAncestor(root, node1, node2);
if (ancestor)
cout << ancestor->_value << endl;
else
cout << "没有公共祖先" << endl;
}
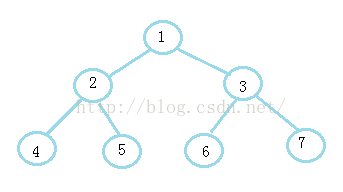
测试用例二叉树