数据结构——图的概述

引言

首先介绍图的基本概念，然后介绍两种实现图的方式，最后探讨一些相关算法。

本文相关代码实现涉及到栈和队列的请访问：栈和队列的实现

基本概念

以下基本概念转自数据结构：图概念与基本图实现

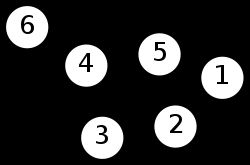
图是由顶点$V$集和边$E$集构成，因此图可以表示成$G=(V,E)$。

就是无向图，我们可以说这张图中，有点集$V=\{1,2,3,4,5,6\}$，边集$E=\{(1,2),(1,5),(2,3),(2,5),(3,4),(4,5),(4,6)\}$。在无向图中，边$(u,v)$和边$(v,u)$是一样的，因此只要记录一个就行了。也就是说方向是无关的。

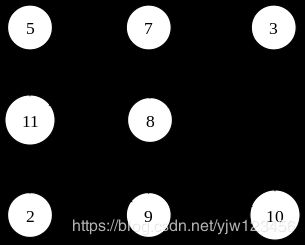
有向图也很好理解，就是加上了方向性，顶点$(u,v)$之间的关系和顶点$(v,u)$之间的关系不同。例如你欠我的钱和我欠你的钱是万万不能混淆的。

加权图：与加权图对应的就是无权图，或叫等权图。如果一张图不含权重信息，我们就认为边与边之间没有差别。不过，具体建模的时候，很多时候都需要有权重，比如对中国重要城市间道路联系的建模，总不能认为从北京去上海和从北京去广州一样远(等权)。

完全图：每一对顶点间都存在一条边的图。

无向图中，任意两个顶点间都有边，称为无向完全图。

• 两个重要关系：

  • 邻接(adjacency)：邻接是两个顶点之间的一种关系。如果图包含$(u,v)$，则称顶点$v$与顶点$u$邻接。当然，在无向图中，这也意味着顶点$u$与顶点$v$邻接。
  • 关联(incidence)：关联是边和顶点之间的关系。在有向图中，边$(u,v)$从顶点$u$开始关联到$v$，或者相反，从$v$关联到$u$。

注意，有向图中，边不一定是对称的，有去无回是完全有可能的。细化这个概念，就有了顶点的入度(in-degree)和出度(out-degree)。无向图中，顶点的度就是与顶点相关联的边的总数，没有入度和出度。在有向图中，我们以上图为例，顶点10有2个入度，$3\to 10$，$11\to 10$，但是没有从10指向其它顶点的边，因此顶点10的出度为0。

路径(path)：依次遍历顶点序列之间的边所形成的轨迹。注意，依次就意味着有序，先1后2和先2后1不一样。
简单路径：没有重复顶点的路径称为简单路径。说白了，这一趟路里没有出现绕了一圈回到同一点的情况，也就是没有环。

环：包含相同的顶点两次或者两次以上。上图中的顶点序列$<1,2,4,3,1>$，1出现了两次，当然还有其它的环，比如$<1,4,3,1>$。
无环图：没有环的图，其中，有向无环图有特殊的名称，叫做DAG(Directed Acyline Graph)（最好记住，DAG具有一些很好性质，比如很多动态规划的问题都可以转化成DAG中的最长路径、最短路径或者路径计数的问题）。

连通的：无向图中每一对不同的顶点之间都有路径。如果这个条件在有向图里也成立，那么就是强连通的。下图中的图不是连通的，因为看到$a$和$d$之间没有通路。

连通分量：不连通的图是由2个或者2个以上的连通子图组成的。这些不相交的连通子图称为图的连通分量。

比如下图中有三个连通分量

有向图的连通分量：如果某个有向图不是强连通的，而将它的方向忽略后，任何两个顶点之间总是存在路径，则该有向图是弱连通的。若有向图的子图是强连通的，且不包含在更大的连通子图中，则可以称为有向图的强连通分量。
下图中，$a$、$e$没有到$\{b,c,d\}$中的顶点的路径，所以各自是独立的连通分量。因此，图中有三个强连通分量，用集合写出来就是：$\{\{a\},\{e\},\{b,c,d\}\}$（已经用不同颜色标出）。

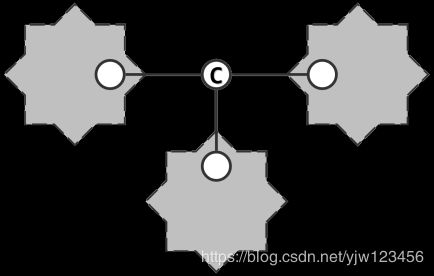
关节点(割点)：某些特定的顶点对于保持图或连通分支的连通性有特殊的重要意义。如果移除某个顶点将使图或者分支失去连通性，则称该顶点为关节点。如下图中的$c$。

关节点的重要性不言而喻。如果你想要破坏互联网，你就应该找到它的关节点。同样，要防范敌人的攻击，首要保护的也应该是关节点。在资源总量有限的前提下，找出关节点并给予特别保障，是提高系统整体稳定性和鲁棒性的基本策略。
桥(割边)：和关节点类似，删除一条边，就产生比原图更多的连通分支的子图，这条边就称为割边或者桥。

实现方式

常见的实现方式有两种

邻接矩阵

假定图中顶点数为v,邻接矩阵通过长、宽都为v的二维数组实现，若稀疏图(图中边的数目较少)通过邻接矩阵，会浪费很多内存空间。

邻接链表

通过代码实现时，我们进行一个优化，不使用链表这种数据结构，而是用集合（不会存在相同元素）。这种实现方式也可以叫做邻接集。

无向图的邻接链表实现见： 无向图的邻接集实现

有向图的邻接链表实现见： 有向图的邻接集实现

相关算法

无向图

无向图的深度优先搜索和广度优先搜索寻路

无向图的连通分量计算

有向图

在有向图中，边是有方向的。有向图中，顶点的出度为该顶点出发的边的总数，入度为指向该顶点的边的总数。

我们重点学习下有向图的算法，有：

• 有向图的可达性与寻路
• 环和有向无环图相关算法 包括调度问题、检测是否有环、拓扑排序
• 有向图的强连通分量计算算法详解

最小生成树

加权图是一种为每条边关联一个权值(可表示成本、时间等)的图模型。这种图能表示许多场景，如航空图中边表示航线，权值表示距离或费用。在航空图中，通常的问题是如何使距离或费用最小化。

我们可以通过加权无向图的最小生成树来解决这个问题。

图的生成树：是它的一颗含有其他所有顶点的无环连通子图。一幅加权无向图的最小生成树(MST)是它的一颗权值最小的生成树(树中所有边的权值之和最小)。

我们会一起学习计算最小生成树的两种经典算法：Prime算法和Kruskal算法。

首先有几个注意点：

• 只考虑连通图
• 边的权值可以表示距离、时间、费用或其他变量
• 边的权重可能是0或负数
• 所有边的权重都不相同

我们要在一幅加权连通无向图中找到它的最小生成树。

首先定义一下加权无向图的数据结构

最小生成树算法：Prim算法和Kruskal算法

最短路径

我经常用百度地图来获取从A地到B地最快的走法是什么。该问题的其实就是最短路径问题：找到从一个顶点到达另一个顶点的成本(时间)最小的路径。

我们采用加权有向图模型作为数据结构。

在一幅加权有向图中，从顶点s到顶点t的最短路径是所有从s到t的路径中的权重最小者

单点最短路径：给定一幅加权有向图和一个起点s，找出最短(总权重最小)的那条路径。

首先定义加权有向图的数据结构

然后给出图的最短路径算法实现