Trie树(基础操作）

开始写这篇文章的时候，其实也是初学，trie树是那个时候唯一听得懂得了…

当时就初一吧…，所以还拿3D画图贴纸，也是消磨时光，结果就骗了这么多访问…

现在初三啦，有点惭愧啊，所以决定在保留原版本的基础上再写一篇。

远古版本。

远古版本

Trie树：

概念什么的，请百度。
一棵树，26叉树，子节点都代表字符。
我觉得吧，这就是将字符串用树的方式存储，以便于操作。忽略根结点，那么第一层就都是字符串的第一个字母，第二层是第二个，以此类推。例如字符串“achq”就可以存储成这样

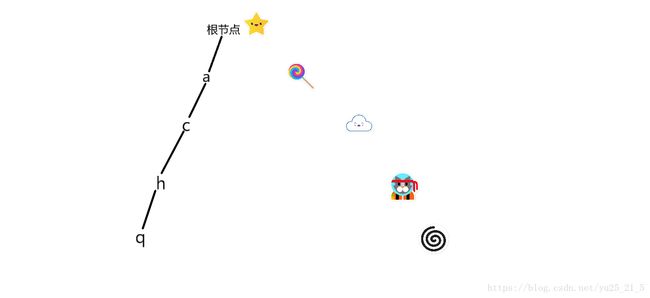
如果再加入一个字符串“abcd"这棵树就变成了这样

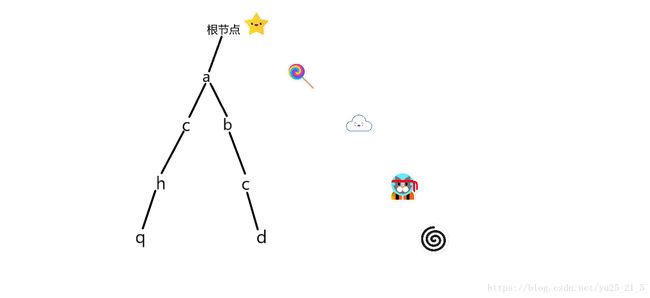
根据顺序还有个编号，于是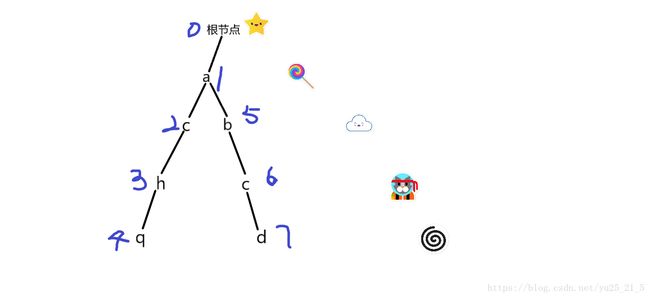

给定n个字符串，再给定Q个询问，每次询问某个字符串在这n个字符串中出现了多少次？"

trie树可以应用于这类问题，可以统计一个数组sum[now]表示以编号为now的这个字符结尾的字符串出现的次数。如上图中sum[4]=1;sum[7]=1;
由上图可知，要到达编号为7的字母就必须到达编号为6的字母，要到达编号为6的字母就必须到达编号为5字母，要到达编号为5的字母就必须到达编号为1的字母。综上所述，若要到达编号为7的字母，则要经过的点的编号为1567，即字符串必须为abcd。所以只要结尾字符编号相同字符串就相同。

建立一棵trie树：

从根节点开始往下，从字符串的第一个字母开始，如果根节点下一层已经有这个字母就走到这个节点，不然就新建立这个节点，直到字符串的末尾结束。我们建立一个二维的a数组，若a[i][j]=0则表示编号为i的节点下没有子节点字母j（一般用数字表示，如可以将‘a’表示为1,'b’表示为2），否则为编号为i的节点下字母j的编号。根节点不代表任何字母。

#include 
using namespace std;
int n,t=0,a[10000][10000];
string str;
void insert(int now,int k)
//now为当前所在节点的编号，k表示字符串的下标
{
    if (k==str.size()) return;//已到字符串结尾，结束
	if (a[now][int(str[k]-96)!=0]) 
	   insert(a[now][int(str[k]-96)],k+1);//已有这个节点，走下去
	else 
	{
		a[now][int(str[k]-96)]=++t;//建立这个节点，t为这个节点的编号
		insert(a[now][int(str[k]-96)],k+1);//走下去
    }//没有这个节点
    return ;
}
int main()
{
	cin>>n;
    for (int i=1;i<=n;i++)
	{
	    cin>>str;
		insert(0,0);//从根节点开始，字符串第一位开始
    }
    return 0;
}
    

上面那道题：

这道题，就要应用一下sum数组啦

#include 
using namespace std;
int n,t=0,a[10000][10000],q,sum[10000];
string str;
void insert(int now,int k)
{
    if (k==str.size()) 
	{
	    return;
	    sum[now]++;
	} 
	if (a[now][int(str[k]-96)!=0]) insert(a[now][int(str[k]-96)],k+1);
	else 
	{
		a[now][int(str[k]-96)]=++t;
		insert(a[now][int(str[k]-96)],k+1);
    }
    return ;
}
int find(int now,int k)
{
    if (k==str.size()) return sum[now];
    if (a[now][int(str[k]-96)]!=0) return 0;
	  else return find(a[now][int(str[k]-96)],k+1); 
}
int main()
{
	cin>>n;
    for (int i=1;i<=n;i++)
	{
	    cin>>str;
		insert(0,0);
    }
    cin>>q;
    for (int i=1;i<=q;i++)
	{
	   cin>>str;
	   cout<<find(0,0);
    }
    return 0;
}
    

ps:代码没有评测过QAQ
例题：
前缀统计
https://www.acwing.com/problem/content/144/
裸题？？
写的时候注意细节

#include 
using namespace std;
int n,m,num=0;
char S[1000010],T[1000010];
int ans;
int a[1000010][30],s[1000010];
void insert(int now,int now_)
{
    if (now==strlen(S)) {s[now_]++;return;}
    if (!a[now_][int(S[now])-96]) a[now_][int(S[now])-96]=++num;
    insert(now+1,a[now_][int(S[now])-96]);
}
void Find(int now,int now_)
{
    ans+=s[now_];
    if (now==strlen(T)) return ;
    if (!a[now_][int(T[now])-96]) return ; 
    Find(now+1,a[now_][int(T[now])-96]);
}
int main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++)
    {
        scanf("%s",S);
        insert(0,0);
    }
    for (int i=1;i<=m;i++)
    {
        ans=0;
        scanf("%s",T); 
        Find(0,0);
        printf("%d\n",ans);
    }
    return 0;
}

trie树可以转化为0/1树，也就是说你可以将一个整数拆成二进制然后存到trie树上
例题：
最大异或对
https://www.acwing.com/problem/content/145/
我觉得这道题挺优秀的

#include 
using namespace std;
int a[32*100010][2],num=0,n;
long long s,ans=0;
void Find(long long now,long long now_,long long gg)
{
	if (now==0) return ;
	if (a[now_][!((gg>>(now-1))&1)]) 
	{
		s=s+(1LL<<(now-1));
	    Find(now-1,a[now_][!((gg>>(now-1))&1)],gg);
    }
    else Find(now-1,a[now_][(gg>>(now-1))&1],gg);
}
void insert(long long now,long long now_,long long gg)
{
	if (now==0) return ;
	if (!a[now_][(gg>>(now-1))&1]) a[now_][(gg>>(now-1))&1]=++num;
	insert(now-1,a[now_][(gg>>(now-1))&1],gg);
}
int main()
{
	cin>>n;
	for (int i=1;i<=n;i++)
	{
		long long x;
		cin>>x;
		s=0;
		if (i!=1) Find(32,0,x);
		insert(32,0,x);
		ans=max(ans,s);
    }
    cout<<ans;
    return 0;
}

升级版：
最长异或值路径
https://www.acwing.com/problem/content/146/
咳咳，我还没写

可持久化trie树

这个我好想还不是很懂的说，参考可持久化线段树？？

新

---

基础操作

其实就是你想要建一棵树，这棵树需要支持你插入一个单词，查询某个单词出现了多少次。

所以我们用边来代表字符，一个节点所代表的的字符串就是从根走到这个节点，途中所经过的边（每条边都代表了某一个字符）的字符组成的字符串。具体可以参考远古版本中的图。

所以trie树是一棵26叉的树

所以现在就是插入，查询的问题了。思路其实较简单。

插入，有边就走，没有边就新建啊，走完了就给对应的节点++，表示以这个节点结尾的字符串多了1个。

显然不会有两个节点对于相同的字符串，一个节点对应的字符串也是惟一的（它是棵树啊！）

查询，就是找到对应这个字符串的是哪个节点，如果没有这个节点那么肯定就没有出现过啊。

大括号换行，用递归写trie好丑啊啊啊啊。

看代码就懂了（如果你想看递归版，可以看远古版本里的）