吴恩达机器学习线性回归练习题：多变量线性回归（python实现）

练习题背景：网易云课堂->吴恩达机器学习课程->线性回归练习题->多变量线性回归

对于练习题的详细内容，和课程中推荐的octave编程实现，请见：吴恩达机器学习线性回归练习题：多变量线性回归（octave实现）

这边只贴出整个多变量线性回归步骤的Python实现代码，每个步骤在代码中有注释说明，变量和函数的命名也基本与练习题资料一致。

全部代码：

import pandas
import numpy
import matplotlib.pyplot as plt


def featureNormalization(X):
    """
    数据标准化
    :param X:
    :return:
    """
    mu = numpy.mean(X, axis=0)
    # ddof的设置，会改变标准差的结算结果，因为总体误差和样本误差的计算公式不一样
    sigma = numpy.std(X, axis=0, ddof=1)

    X_norm = (X - mu) / sigma

    return X_norm, mu, sigma


def computeCostMulti(X, y, theta):
    """
    计算损失函数
    :param X:
    :param y:
    :param theta:
    :return:
    """
    m = X.shape[0]
    costs = X.dot(theta) - y
    total_cost = costs.transpose().dot(costs) / (2 * m)
    return total_cost[0][0]


def gradientDescentMulti(X, y, theta, alpha, iterNum):
    """
    梯度下降实现
    :param X:
    :param y:
    :param theta:
    :param alpha:
    :param iterNum:
    :return:
    """
    m = len(X)

    J_history = list()

    for i in range(0, iterNum):
        costs = X.dot(theta) - y
        theta = theta - numpy.transpose(costs.transpose().dot(X) * (alpha / m))

        J_history.append(computeCostMulti(X, y, theta))

    return theta, J_history


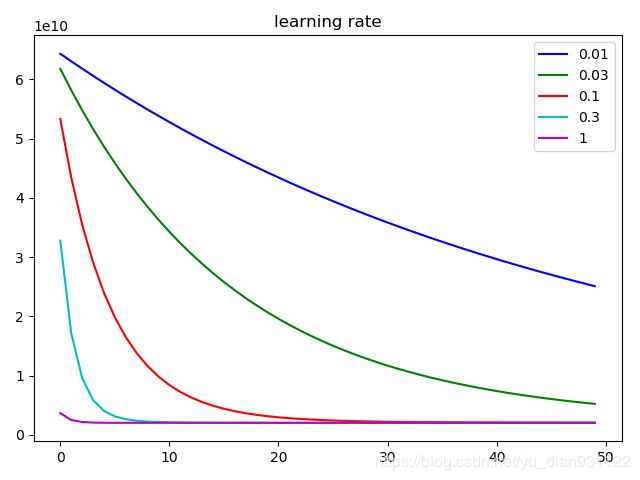
def learningRatePlot(X_norm, y):
    """
    不同学习速率下的梯度下降比较
    :param X_norm:
    :param y:
    :return:
    """
    colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k']
    plt.figure()
    iter_num = 50
    # 如果学习速率取到3，损失函数的结果随着迭代次数增加而发散，值越来越大，不太适合在同一幅图中展示
    for i, al in enumerate([0.01, 0.03, 0.1, 0.3, 1]):
        ta = numpy.zeros((X_norm.shape[1], 1))
        ta, J_history = gradientDescentMulti(X_norm, y, ta, al, iter_num)

        plt.plot([i for i in range(len(J_history))], J_history, colors[i], label=str(al))

    plt.title("learning rate")
    plt.legend()
    plt.show()


def normalEquation(X, y):
    """
    正规方程实现
    :param X:
    :param y:
    :return:
    """
    return numpy.linalg.inv(X.transpose().dot(X)).dot(X.transpose()).dot(y)


if __name__ == '__main__':
    # 读取数据
    data_path = r'D:\ML\AndrewNg\machine-learning-ex1\ex1\ex1data2.txt'
    data = pandas.read_csv(data_path, delimiter=",", header=None)

    # 切分特征和目标， 注意：索引是从0开始的
    X = data.iloc[:, 0:2].values
    y = data.iloc[:, 2:3].values

    # 数据标准化
    X_norm, mu, sigma = featureNormalization(X)

    ones = numpy.ones((X_norm.shape[0], 1))

    # 假设函数中考虑截距的情况下，给每个样本增加一个为1的特征
    X_norm = numpy.c_[ones, X_norm]

    # 初始化theta
    theta = numpy.zeros((X_norm.shape[1], 1))

    # 梯度下降学习速率为0.01
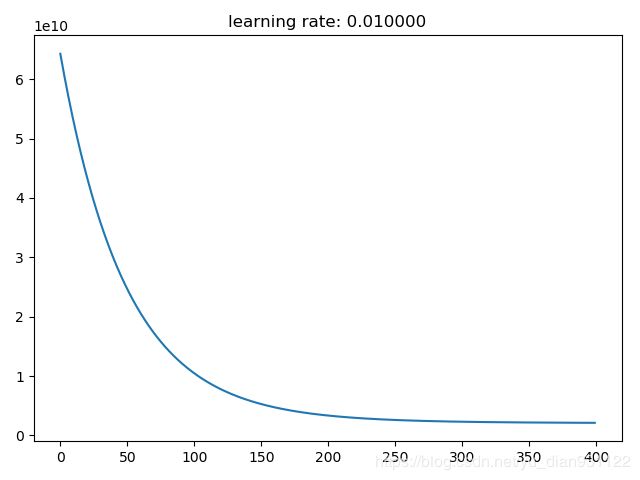
    alpha = 0.01
    # 梯度下降迭代次数为400
    iterNum = 400

    # 梯度下降
    theta, J_history = gradientDescentMulti(X_norm, y, theta, alpha, iterNum)

    # 画出梯度下降过程中的收敛情况
    plt.figure()
    plt.plot([i for i in range(len(J_history))], J_history)
    plt.title("learning rate: %f" % alpha)
    plt.show()

    # 使用不同学习速率下的收敛情况
    learningRatePlot(X_norm, y)

    # 预测面积为1650，卧室数量为3的房子价格
    x_pre = numpy.array([1650, 3])

    x_pre_norm = (x_pre - mu) / sigma
    numpy_ones = numpy.ones((1,))
    x_pre_norm = numpy.concatenate((numpy.ones((1,)), x_pre_norm))
    price = x_pre_norm.dot(theta)
    print("通过梯度下降求解的参数预测面积1650、卧室数量3的房子价格为：%f" % price[0])

    # 下面使用正规方程计算theta
    X_ = numpy.c_[ones, data.iloc[:, 0:2].values]
    y_ = data.iloc[:, 2:3].values

    theta = normalEquation(X_, y)

    # 预测面积为1650，卧室数量为3的房子价格
    x_pre = numpy.array([1, 1650, 3])
    price = x_pre.dot(theta)
    print("通过正规方程求解的参数预测面积1650、卧室数量3的房子价格为：%f" % price[0])

代码执行结果：

通过梯度下降求解的参数预测面积1650、卧室数量3的房子价格为：289314.620338
通过正规方程求解的参数预测面积1650、卧室数量3的房子价格为：293081.464335

代码运行过程中会生成两张图：

• 迭代次数为400，学习速率为0.01时，梯度下降的收敛情况：
• 迭代次数为50时，不同学习速率下梯度下降的收敛情况：