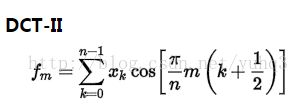关于图像压缩实验
图像压缩实验报告
一、背景介绍【1】
图像压缩是数据压缩技术在数字图像上的应用,目的是减少图像数据中的冗余信息,从而用更加高效的格式存储和传输数据。而图像压缩的方法可以是有损压缩或无损压缩,常见的应用有gif和tiff格式等。
有损压缩又称“破坏性资料压缩”、“不可逆压缩”,通过这种压缩方法,解压后的数据会与原始数据不同但非常相近,借由将次要的信息数据舍弃,牺牲一些质量来减少数据量、提高压缩比。根据各种格式设计的不同,有损压缩都会有代间损失——每次压缩与解压文件都会带来渐进的质量下降。在很多情况下,数据会包含比必要的还多的信息。例如,一张分辨率过高的照片,其中的细节肉眼可能已无法辨识;同理,在一个音量很高的音频片段中,一些细节可能是人耳难以察觉的。舍弃这些人类无法察觉的细节,就可以用更小的数据量,提供与原始数据相差无几的感官体验。有时也允许失去一部分可以察觉的细节,来达到更好的压缩率。
无损压缩是指数据经过压缩后,信息不受损失还能完全恢复到压缩前的原样。无损”一词是相对于有损数据压缩,有损数据压缩只允许一个近似原始数据进行重建,以换取更好的压缩率。无损压缩通常用于严格要求“经过压缩、解压缩的数据必须与原始数据一致”的场合。我们可以借由无损压缩,在不失去任何信息的条件下,将数据压缩得更小。例如,当一张图片存储成数字文件时,我们会将它转换成一连串的点,再分别存储每个点的颜色信息。如果某张图片由200个红点构成,我们会以类似“红点、红点、...(重复197次)...、红点”的格式来存储它。在这个例子中,我们可以改成用“200个红点”这样的格式来存储这张图片,就能不失去任何信息的完成压缩。然而,若要保留源文件案的所有信息,信息论说明了,无论使用任何压缩方法,文件大小都无法低于一个下界。一个直观的例子:压缩后得到的zip文件会比源文件案更小,但一直重复压缩同一个文件并不会让文件大小变成0,因为源文件案终究含有一定量的信息。
二、回顾算法【2】
①游程编码(无损压缩)【3】:Run-Length Coding,又称行程长度编码或变动长度编码法,是一种与资料性质无关的无损数据压缩技术。变动长度编码法为一种“使用变动长度的码来取代连续重复出现的原始资料”的压缩技术。举例来说,一组资料串"AAAABBBCCDEEEE",由4个A、3个B、2个C、1个D、4个E组成,经过变动长度编码法可将资料压缩为4A3B2C1D4E(由14个单位转成10个单位)。简言之,其优点在于将重复性高的资料量压缩成小单位;然而,其缺点在于─若该资料出现频率不高,可能导致压缩结果资料量比原始资料大,例如:原始资料"ABCDE",压缩结果为"1A1B1C1D1E"(由5个单位转成10个单位)。
其算法步骤如下:先使用一个暂存函数Q读取第一个资料,接着将下一个资料与Q值比,若资料相同,则计数器加1;若资料不同,则将计数器存的数值以及Q值输出,再初始计数器为,Q值改为下一个资料。以此类推,完成资料压缩。
②香农范诺编码(无损压缩)【4】:Shannon–Fanocoding,是一种基于一组符号集及其出现的或然率(估量或测量所得),从而构建前缀码的技术。该编码将符号从最大可能到最少可能排序,然后将排列好的符号分化为两大组,使两组的概率和近于相同,并各赋予一个二元码符号“0”和“1”。只要有符号剩余,以同样的过程重复这些集合以此确定这些代码的连续编码数字。依次下去,直至每一组的只剩下一个信源符号为止。当一组已经降低到一个符号时,意味着符号的代码是完整的,不会形成任何其他符号的代码前缀。
其算法步骤如下:1)对于一个给定的符号列表,制定概率相应的列表或频率计数,得到每个符号的相对发生频率。2)根据频率的符号列表排序,最常出现的符号在左边,最少出现的符号在右边。3)清单分为两部分,使左边部分的总频率和尽可能接近右边部分的总频率和。4)该列表的左半边分配二进制数字0,右半边是分配的数字1。5)对左、右半部分递归应用步骤3和4,细分群体,并添加位的代码,直到每个符号已成为一个相应的代码树的叶。
③哈夫曼编码(无损压缩)【5】:HuffmanCoding,是一种用于无损数据压缩的熵编码(权编码)算法。它使用变长编码表对源符号(如文件中的一个字母)进行编码,其中变长编码表是通过一种评估来源符号出现机率的方法得到的,出现机率高的字母使用较短的编码,反之出现机率低的则使用较长的编码,这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。同时它又称最优二叉树,是一种带权路径长度最短的二叉树。
其算法步骤如下:1)为每个符号建立一个叶子节点,并加上其相应的发生频率。2)当有一个以上的节点存在时,进行下列循环:把这些节点作为带权值的二叉树的根节点,左右子树为空;选择两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,且新的二叉树的根结点的权值为其左右子树上根结点的权值之和;把权值最小的两个根节点移除;将新的二叉树加入队列中。3)最后剩下的节点暨为根节点,此时二叉树已经完成。
④算术编码(无损压缩)【6】:ArithmeticCoding,是一种无损数据压缩方法,也是一种熵编码的方法。和其它熵编码方法不同的地方在于,其他的熵编码方法通常是把输入的消息分区为符号,然后对每个符号进行编码,而算术编码是直接把整个输入的消息编码为一个数,一个满足(0.0 ≤ n < 1.0)的小数n。在给定符号集和符号概率的情况下,算术编码可以给出接近最优的编码结果。使用算术编码的压缩算法通常先要对输入符号的概率进行估计,然后再编码。这个估计越准,编码结果就越接近最优的结果。
算法步骤举例如下:1)假设对一个简单的信号源进行观察,得到的统计模型如下: 60%的机会出现符号中性,20%的机会出现符号 阳性 ,10%的机会出现符号 阴性 ,10%的机会出现符号数据结束符. (出现这个符号的意思是解码已完成)。2)则得到符号模型如下:中性对应的区间是[0, 0.6) 阳性对应的区间是[0.6,0.8) 阴性对应的区间是[0.8, 0.9) 数据结束符对应的区间是[0.9,1)。3)假设此时编码为0.538,则它落在子区间[0,0.6)中,这向我们提示编码器所读的第一个符号必然属于中立的,这样我们就可以将它作为消息的第一个符号记下来。4)然后我们将区间[0,0.6)分成子区间: 中性 的区间是[0, 0.36) -- [0, 0.6)的60% ,阳性 的区间是[0.36, 0.48) -- [0, 0.6)的20% ,阴性 的区间是[0.48, 0.54) -- [0, 0.6)的10% ,数据结束符 的区间是[0.54, 0.6). -- [0, 0.6)的10% ,我们的分数.538在[0.48, 0.54)区间;所以消息的第二个符号一定属于阴性的。5)我们再一次将当前区间划分成子区间: 中性 的区间是[0.48, 0.516) 阳性的区间是[0.516, 0.528) 阴性 的区间是[0.528,0.534) 数据结束符 的区间是[0.534, 0.540). 我们的分数.538落在符号数据结束符的区间;所以,这一定是下一个符号。由于它也是内部的结束符号,这也就意味着编码已经结束。
⑤离散余弦变换编码(有损压缩)【7】:Discrete CosineTransform (DCT),是与傅里叶变换相关的一种变换,类似于离散傅里叶变换,但是只使用实数。离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换,这个离散傅里叶变换是对一个实偶函数进行的(因为一个实偶函数的傅里叶变换仍然是一个实偶函数),在有些变形里面需要将输入或者输出的位置移动半个单位(DCT有8种标准类型,其中4种是常见的)。最常用的一种离散余弦变换的类型是下面给出类型,通常我们所说的离散余弦变换指的就是这种。
⑥K-L转换(有损压缩)【8】:Karhunen-Loève Transform,是建立在统计特性基础上的一种转换,它是均方差(MSE, Mean Square Error)意义下的最佳转换,因此在资料压缩技术中占有重要的地位。在影像的压缩上,目的是要将原始的影像档用较少的资料量来表示,由于大部分的影像并不是随机的分布,相邻的像素间存在一些相关性,如果我们能找到一种可逆转换(reversible transformation),它可以去除数据的相关性,如此一来就能更有效地储存资料,由于K-L转换是一种线性转换,它可以对输入的向量x做一个正交变换,使得输出的向量得以去除数据的相关性,因此可以将它应用在影像的压缩上。
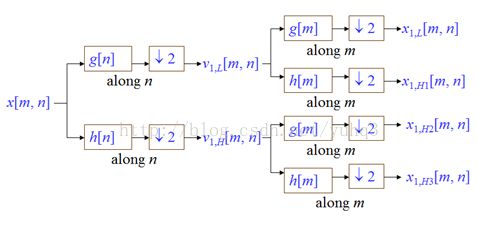
⑦小波压缩(有损压缩)【9】:Wavelet-Based Coding,主要的方式是利用离散小波转换来处理。示例如下:
上图是二维离散小波转换的结构图,输入信号{\displaystyle {\mathit {x[m,n]}}} ,由结构图顺序可以得到:1)先沿n方向做离散小波转换得{\displaystyle {\mathit{v_{1,L}[m,n]}}=\sum _{k=0}^{K-1}x[m,2n-k]g[k]}
2)再沿m方向得{\displaystyle {\mathit{x_{1,L}[m,n]}}=\sum _{k=0}^{K-1}v_{1,L}[2m-k,n]g[k]} {\displaystyle{\mathit {x_{1,H_{1}}[m,n]}}=\sum _{k=0}^{K-1}v_{1,L}[2m-k,n]h[k]}
上述过程即做完一阶二维的离散小波转换。下图是将视频经过处理的结果,可以看出在高频部分,左下角为水平方向的边缘;右上方为垂直方向的边缘;右下方为图形的角落。而左上角为低频,可继续做小波转换,分出更粗略、接近原视频的缩略图,来达到压缩效果。
三、无损压缩Huffman编码和有损压缩JPEG原理及步骤:
1)无损压缩Huffman编码:
在第二节③中已经详细介绍过Huffman编码的原理和步骤,接下来再举个例子:设已得到文件中每个符号(对应每个字节)的出现概率统计情况为

将出现次数多的符号结点作为左子树,出现次数少的符号结点作为右子树,则可得到如下构造Huffman树的过程,以及最终每个符号对应编码的表。
2)有损压缩JPEG:
JPEG压缩是有损压缩,它利用了人的视角系统的特性,使用量化和无损压缩编码相结合来去掉视角的冗余信息和数据本身的冗余信息。其编码过程如下【10】:
①色彩空间转换:首先,视频由RGB(红绿蓝)转换为一种称为YUV的不同色彩空间。(Y成分表示一个像素的亮度,U和V成分一起表示色调与饱和度。)这种编码系统非常有用,因为人类的眼睛对于亮度差异的敏感度高于色彩变化。使用这种知识,编码器(encoder)可以被设计得更有效率地压缩视频。
②缩减取样(Downsampling):上面所作的转换使下一步骤变为可能,也就是减少U和V的成分(也可称为"色度抽样"(chroma subsampling)。在JPEG上这种缩减取样的比例可以是4:4:4(无缩减取样),4:2:2(在水平方向2的倍数中取一个),以及最普遍的4:2:0(在水平和垂直方向2的倍数中取一个)。对于压缩过程的剩余部分,Y、U、和V都是以非常类似的方式来个别地处理。
③离散余弦变换(Discrete cosine transform):下一步,将视频中的每个成分(Y, U, V)生成三个区域,每一个区域再划分成如瓷砖般排列的一个个的8×8子区域,每一子区域使用二维的离散余弦变换(DCT)转换到频率空间。(具体步骤为将8x8子区域里的每个值减128,使其范围变为-128~127,然后使用离散余弦变换和舍位取整得到结果。在结果的8x8子区域里左上角之相当大的数值称为DC系数;其他63个值称为AC系数。然后对所有8×8表格中的DC系数使用差分编码,对AC系数使用进程编码。)
④量化(Quantization):人类眼睛在一个相对大范围区域,容易辨别亮度上细微差异,但是却难以分辨高频率亮度变动的确切强度。这让我们能在高频率成分上极佳地降低信息的数量。简单地把频率领域上每个成分,除以一个对于该成分的常量即可,然后舍位取最接近的整数,这是整个过程中的主要有损运算。以这个结果而言,经常会把很多更高频率的成分舍位成为接近0,而剩下很多会变成小的正或负数。一个普遍的量化矩阵是: 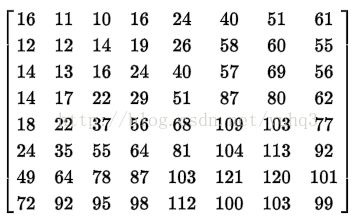 ,然后使用这个量化矩阵与前面所得到的DCT系数矩阵逐项相除得到结果。
,然后使用这个量化矩阵与前面所得到的DCT系数矩阵逐项相除得到结果。
⑤熵编码技术(entropy coding):熵编码是无损数据压缩的一个特别形式。它牵涉到将视频成分以Z字体(zigzag)排列,把相似频率组群在一起(矩阵中往左上方向是越低频率之系数,往右下较方向是较高频率之系数),插入长度编码的零,且接着对剩下的使用霍夫曼编码。 JPEG标准也允许(但是并不要求)在数学上优于霍夫曼编码的算术编码之使用。然而,这个特色几乎很少被使用,因为它被专利所涵盖,且它相较于霍夫曼编码在编码和解码上会更慢。使用算术编码一般会让文件更小约5%。当剩下的所有系数都是零,对于过早结束的序列,JPEG有一个特别的霍夫曼编码用词,EOB。
至此JPEG压缩编码完成,而要使用到压缩的图像时则需要进行解码,即包含反向以上所有操作。
四、实现Huffman编码和JPEG压缩编码(关键代码):
1)Huffman编码【11】:
①首先定义需要建立的Huffman树结点结构,如下所示:
// 二叉树结点
struct TreeNode {
// 频率
unsigned long frequency;
// 深度,编码长度
int length;
// 父结点
TreeNode * parent;
// 左结点
TreeNode * left;
// 右结点
TreeNode * right;
// 字节编码
char * code;
TreeNode() :length(0), frequency(0),code(0), parent(0), left(0), right(0){}
};
②读入bmp图像,使用定义好的缓冲区和其他变量存储图像文件头、长度以及图像内容,并将图像内容(即图像各个像素值)存入各像素值编码的数组中,每次读取一个像素值,对应的像素值结点frequency++。
③读取完毕后,首先根据各像素值frequency大小从小到大排序;然后构建树,从小到大不断两两依次合并,要注意合并之后还需根据frequency插入适当的位置中;最后生成编码。关键代码如下:
// 编码
void HuffmanCode::CreateCode()
{
// 将所有非0次值按指定顺序加入临时队列
for (int i = 0; i < 256; i++)
if (code[i].frequency > 0)
// 将结点按顺序加入临时队列
AddToList(&code[i]);
// 构建树:取出前两个合并为一个结点,并再加入到队列,直到只有一个结点为止
while (NULL != CodeHead&& CodeHead->parent != NULL)
{
// 取出前两个结点
…
// 合并结点
…
// 增加结点儿子深度
AddChildLen(p);
// 将结点按顺序加入临时队列
AddToList(p);
}
// 构建树完成,生成编码
for (int i = 0; i < 256; i++)
if (code[i].frequency > 0)
CreateCode(&code[i]);
}
// 生成结点编码
void HuffmanCode::CreateCode(TreeNode* pNode)
{
// 没有,则不需要空间
…
// 只有一个节点的情况。即只有一个字符出现过
if (pNode->length == 0)
{
…
}
else
{
// 左儿子为1
…
// 右儿子为0
…
}
}
④在输出文件中写入之前存储好的文件头、文件长度以及上一步得到的以0、1字符串形式表示的编码表,即可得到根据huffman编码完成的无损压缩图像。
⑤当需要显示压缩图像时,将上述流程逆操作即可。
2)JPEG编码【12】:
①首先分离RGB颜色分量,并将其转换到YUV颜色空间。
②将图像分为8*8的block,并对每个block进行DCT变换:
%产生一个 8*8 的 DCT 变换矩阵
T=dctmtx(8);
%进行 DCT 变换 BY BU BV 是 double 类型
BY=blkproc(Y,[88],'P1*x*P2',T,T');
BU=blkproc(U,[88],'P1*x*P2',T,T');
BV=blkproc(V,[88],'P1*x*P2',T,T');
③分别声明低频分量量化表a和高频分量量化表b,并使用a对Y分量进行量化,使用b对U、V分量进行量化:
BY2=blkproc(BY,[8 8],'round(x./P1)',a);
BU2=blkproc(BU,[8 8],'round(x./P1)',b);
BV2=blkproc(BV,[8 8],'round(x./P1)',b);
④分别对三个分量数组使用Z字型顺序重新排列,将数组最后一个非0元素舍弃,并加上结束标记,压缩完成:
%将8x8 的块转化为列
y =im2col(x, [8 8], 'distinct');
%分块数
xb =size(y, 2);
%按照order的顺序排列数据
y =y(order, :);
%设置块尾结束标志
eob =max(y(:)) + 1;
r =zeros(numel(y) + size(y, 2), 1);
%计数
count= 0;
%每次处理一个块,找到最后一个非零元素,加入块结束标志
for j =1:xb
…
end
%删除r中不需要的元素
r((count+ 1):end) = [];
⑤当需要显示压缩图像时,将上述流程逆操作即可。
五、实验结果:
1)Huffman编码:
图1 文件大小
如图1所示,t1.bmp为输入图像,t2.bmp为输出图像,可以看到大小都是1,407KB,证明Huffman编码确实是无损编码;hfm文件是输入图像压缩后的文件,大小为1,288KB。因此可以计算得到,Huffman编码压缩了大概100KB,压缩率为91.5%,没有失真。
输入图像与输出图像如图2,3所示,因为是无损压缩,所以恢复原图后视觉上也不会有任何变化。
图2 输入图像
图3 输出图像
2)JPEG编码:
图4 文件大小
如图4所示,t1.bmp是输入图像,t2.jpg是输出图像,大小分别是1,407KB和49KB,可见JPEG有损压缩具有非常高的压缩比,其压缩比为3.5%,根据公式 得,失真率SNR为29.6。
得,失真率SNR为29.6。
图5 输入图像
图6 输出图像
输入图像与输出图像如图5,6所示,尽管压缩了将近97%的大小,但视觉上变化并不大,但如果仔细观察还是可以发现输出图像比输入图像要淡一些,这也正是在YUV颜色空间上减弱了UV分量所导致的。
六、总结:
从第五节的实验结果可以看到,JPEG编码压缩和解压缩之后得到的图像,与原图差距不大,然而在压缩率上远远超过了Huffman编码。针对这次实验结果,我认为有如下原因:
1)Huffman编码属于无损压缩,JPEG编码属于有损压缩,在不能失去任何信息的前提下,Huffman编码只能做到减少冗余表示这一层,极大地限制了可以被压缩的空间。而JPEG编码不受无损的限制,可以在像素颜色分量层面忽略许多高频细节信息,使得这些细枝末节的部分全部省略,大大地压缩了表示空间。
2)在用C++实现Huffman编码进行图像压缩时,没有在真正意义上将每一个像素值以一个位的形式存储起来,而是用char(实际是1个字节8位)存储,这样就占据了很多空间。
3)在用Matlab实现JPEG编码进行图像压缩时,使用了imwrite函数以.jpg形式存储输出图像,可能会使得输出图像在通过jpeg编码后再次用matlab自带的编码重新压缩一遍,于是我在不进行任何处理下直接使用imwrite函数对原图以.jpg形式储存,如图4所示中的directimg.jpg,可以看到只有59KB,这也证明了imwrite函数在对不同格式的图像文件操作时确实具有压缩功能。
尽管有如上原因或多或少干扰了本次实验结果,但对于无损压缩和有损压缩各自的优点和缺点在这次实验也能稍显区别:如果想要图像经过压缩和解压缩后能完全保持原图的所有细节信息,应该选择无损压缩,例如在朋友圈晒照片、将图像作为壁纸等情况;如果不追求图像经过压缩和解压缩后显示的质量,而在于存储空间时,则应该选择有损压缩,例如传输大量文件、快速显示当前页面所有图像等情况。
参考文献
【1】维基百科:图像压缩、有损数据压缩、无损数据压缩
【2】Li Z N, Drew M S, LiuJ. Fundamentals of multimedia. 2nd ed[J]. Technology Literacy Applications inLearning Environments, 2004.
【3~10】维基百科:游程编码、香农-范诺编码、哈夫曼编码、算术编码、离散余弦变换、K-L 转换、小波压缩、JPEG
【11】http://bbs.csdn.net/topics/300165376
【12】http://blog.csdn.net/geekzph/article/details/53105858