机器学习入门——使用TensorFlow搭建一个简单的神经网络实现非线性回归

TensorFlow是一个基于数据流编程的符号数学系统，被广泛应用于各类机器学习算法的编程实现。

回归是一种基本算法，也是机器学习中比较重要的内容。

回归的英文是regression，单词原型regress的意思是“回退，退化，倒退”。其实 regression——回归分析的意思是借用里面“倒退，倒推”的含义。简单说就是“由果索因” 的过程，是一种归纳的思想——当我看到大量的事实所呈现的样态，我推断出原因或客观蕴含的关系是如何的；当我看到大量的观测而来的向量是某种样态，我设计一种假说来描述它们之间蕴含的关系是如何的。

在机器学习领域，最常用的回归有两大类----类是线性回归，一类是非线性回归。

所谓线性回归，就是在观察和归纳样本的过程中认为向量和最终的函数值呈现线性的关系。而后设计这种关系为：

y=f(x)=Wx+b

这里的W和x分别是1*n和n*1的矩阵，Wx则指的是这两个矩阵的内积。具体一点说， 例如，如果你在一个实验中观察到一名病患的几个指标呈现线性关系（注意这个是大前提， 如果你观察到的不是线性关系而用线性模型来建模的话，会得到欠拟合的结果）。拿到的x是一个5维的向量，分别代表一名患者的年龄、身高、体重、血压、血脂这几个指标值，y 标签是描述他们血糖程度的指标值，x和y都是观测到的值。在拿到大量样本（就是大量的 x和y)后，我猜测向量（年龄，身髙，体重，血压，血脂）和与其有关联关系的血糖程度y值有这样的关系：

y= w1*年龄+ w2*身高+w3*体重+w4*血压+ w5*血脂+b

那么就把每一名患者的（年龄，身高，体重，血压，血脂）具体向量值代入，并把其血糖程 度少值也代入。这样一来，在所有的患者数据输入后，会出现一系列的六元一次方程，未 知数是w1~w5和b——也就是W矩阵的内容和偏置b的内容。而下面要做的事情就是要对 w矩阵的内容和偏置b的内容求出一个最“合适”的解来。这个“合适”的概念就是要得 到一个全局范围内由/(x)映射得到的y和我真实观测到的那个y的差距加和，写出来是这种方式：

Loss=Σ|Wxi+b-yi|

怎么理解这个的含义呢？加和的内容是Wxi+b和yi的差值， 每一个训练向量xi在通过我们刚刚假设的关系f(Wx+b) 映射后与实际观测值yi的差距值。取绝对值的含义就是指这个差距不论是比观测值大还是比观测值小，都是一样的差距。 将全局范围内这n个差距值都加起来，得到所谓的总差距值，就是这个的含义。那么 显而易见，如果映射关系中W和b给的理想的话，这个差距值应该是0,因为每个X经过 映射都“严丝合缝”地和观测值一致了——这种状况太理想了，在实际应用中是见不到的。 不过，Loss越小就说明这个映射关系描述越精确，这个还是很直观的。那么想办法把Loss描述成：

Loss=f(W, b)

再使用相应的方法找出保证Loss尽可能小的W和b的取值，就算是大功告成了。一旦得到一 个误差足够小的W和b,并能够在验证用的数据集上有满足当前需求的精度表现后就可以了。例如，预测病患的血糖误差是取误差平均小于等于0.3为容忍上线，训练后在验证集上的表现是误差平均为0.2,那就算是合格了。

非线性回归训练的过程跟普通线性回归也是一样的，只不过损失函数的形式不同。但是，它的损失函数的含义仍旧是表示这种拟合残差与待定系数的关系，并通过相应的手段进行迭代式的优化，最后通过逐步调整待定系数减小残差。

 

import tensorflow as tf #导入TensorFlow
import numpy as np#导入Numpy
import matplotlib.pyplot as plt#导入Matplotlib
#使用numpy生成200个随机点
x_data = np.linspace(-0.5,0.5,200)[:,np.newaxis]
#添加随机噪声
noise = np.random.normal(0,0.02,x_data.shape)
y_data = np.square(x_data) + noise

#定义两个占位符（placeholder）
x = tf.placeholder(tf.float32,[None,1])
y = tf.placeholder(tf.float32,[None,1])

#定义神经网络中间层，10个神经元
#变量参数用tf.Variable表示
Weights_L1 = tf.Variable(tf.random_normal([1,10]))#权重
biases_L1 = tf.Variable(tf.zeros([1,10]))#偏置
Wx_plus_b_L1 = tf.matmul(x,Weights_L1) + biases_L1
L1 = tf.nn.tanh(Wx_plus_b_L1)#tanh激励函数

#定义神经网络输出层
Weights_L2 = tf.Variable(tf.random_normal([10,1]))
biases_L2 = tf.Variable(tf.zeros([1,1]))
Wx_plus_b_L2 = tf.matmul(L1,Weights_L2) + biases_L2
prediction = tf.nn.tanh(Wx_plus_b_L2)

#二次代价函数
loss = tf.reduce_mean(tf.square(y-prediction))
#使用梯度下降法训练
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

#创建一个会话（Session）
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())#初始化所有变量，分配内存
    #进行2000次梯度下降优化
    for _ in range(2000):
        sess.run(train_step,feed_dict={x:x_data,y:y_data})#将x_data和y_data喂给tf变量x，y
        
    #获得预测值
    prediction_value = sess.run(prediction,feed_dict={x:x_data})
    #画图
    plt.figure()
    plt.scatter(x_data,y_data)
    plt.plot(x_data,prediction_value,'r-',lw=5)
    plt.xticks(color='white')
    plt.yticks(color='white')
    plt.xlabel('x',fontproperties = 'Times New Roman', fontsize=20, fontstyle = 'italic', color='white')
    plt.ylabel('y',fontproperties = 'Times New Roman', fontsize=20, fontstyle = 'italic', color='white')
    plt.show()

 该程序的神经网络结构如下：

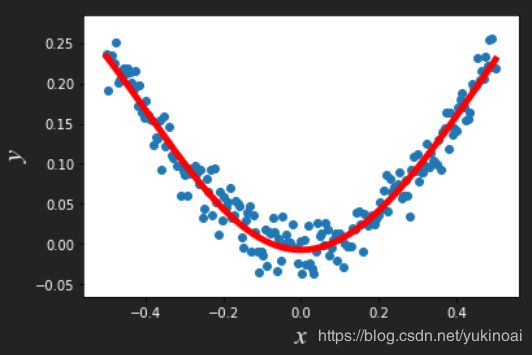
 结果如下，蓝色散点为样本，红色曲线为回归曲线