【定位】正态分布变换（NDT）配准与无人车定位

作者简介：申泽邦（Adam Shan），兰州大学在读硕士研究生，主攻无人驾驶，深度学习；
原文链接：http://blog.csdn.net/adamshan/article/details/79230612

定位即确定无人车在这个世界中的哪个位置，是无人驾驶技术栈中必不可少的一部分。对于无人车而言，对定位的要求极高，一般情况下，我们希望我们的无人车能够达到 厘米级 的定位精度，单纯使用GPS能够达到米级别的定位，显然，无人车的定位模块需要其他的技术支持以进一步提高定位的精度。本文介绍一种依赖于高精度地图和激光雷达的定位技术——正态分布变换（Normal Distributions Transform， NDT）。它能实现满足无人车需求的厘米级的定位需求。

无人车系统中的定位问题

无人车的定位问题，实际上就是要找出无人车当前在地图的那个位置（并且要求精度在厘米级别）。其中有一类方法被称为即时定位与地图构建（simultaneous localization and mapping，SLAM），它能够实现导航定位而不需要地图，然而，真正实现无人车的SLAM是非常困难的，作为交通工具，远距离的行驶会使得实时构建地图的偏差变大。所以，在已经拥有高精度地图的前提下去做无人车的定位，是更加现实，简单的。NDT就是一类利用已有的高精度地图和激光雷达实时测量数据实现高精度定位的技术。

NDT配准的大致理念

下图是一个高精度点云地图的例子：

下图是一个Lidar扫描点云的例子：

通过正态分布变换配准，能够确定车辆当前在高精度地图中的位置，如下图所示：

放大之后：

可以看出，为了知道我们在这个地图中的确切位置，我们比较lidar扫描得到的点云和我们的地图点云，其中一个问题在于：lidar扫描得到的点云可能和地图的点云存在细微的区别，这里的偏差可能来自于测量误差，也有可能这个“场景”发生了一下变化（比如说行人，车辆）。NDT配准就是用于解决这些细微的偏差问题。

NDT并没有比较两个点云点与点之间的差距，而是先将参考点云（即高精度地图）转换为多维变量的正态分布，如果变换参数能使得两幅激光数据匹配的很好，那么变换点在参考系中的概率密度将会很大。因此，可以考虑用优化的方法求出使得概率密度之和最大的变换参数，此时两幅激光点云数据将匹配的最好。

NDT算法

多元正态分布

我们知道，如果随机变量X满足正态分布(即 $X\sim N(\mu ,\sigma )$,则其概率密度函数为：
$$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
其中的$\mu$为正态分布的均值，${\sigma }^2$为方差，这是对于维度D=1的情况而言的。对于多元正态分布而言，其概率密度函数可以表示为：

其中 $x$ 就表示均值向量，而$\Sigma$表示协方差矩阵,我们知道，协方差矩阵对角元素表示的是对应的元素的方差，非对角元素则表示对应的两个元素（行与列）的相关性。

下图表示一个二元的正态分布，

NDT算法流程

网格化并计算正态分布参数

NDT算法的第一步就是将参考点云网格化（对于三维地图来说，即使用一个一个小立方体对整个空间的扫描点进行划分），对于每一个网格（cell）,基于网格内的点计算其概率密度函数（probability density function, PDF）,

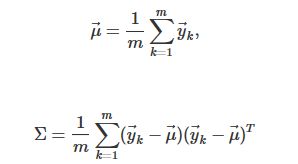
其中， $y_{k=1,...,m}$表示一个网格内所有的扫描点。那么一个网格的概率密度函数则为：

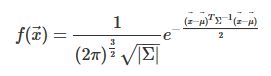
使用正态分布来表示原本离散的点云有诸多好处，这种分块的（通过一个个cell）光滑的表示是连续可导的，每一个概率密度函数可以被认为是一个局部表面（local surface）的近似,它不但描述了这个表面在空间中的位置，同时还包含了这个表面的方向和光滑性等信息。下图是一个3D点云及其网格化效果:

上图中立方体的边长为 1 米，其中越明亮的位置表示概率越高。此外，局部表面的方向和光滑性则可以通过协方差矩阵的特征值和特征向量反映出来。我们以三维的概率密度函数为例，如果三个特征值很接近，那么这个正态分布描述的表面是一个球面，如果一个特征值远大于另外两个特征值，则这个正态分布描述的是一条线，如果一个特征值远小于另外两个特征值，则这个正态分布描述的是一个平面。下图描述了协方差矩阵特征值和表面形状之间的关系：

变换参数和最大似然

当使用NDT配准时，目标是找到当前扫描的姿态，使当前扫描的点位于参考扫描（3D地图）表面上的可能性最大化。那么我们需要优化的参数就是对当前扫描的点云的变换（旋转，平移等），我们使用一个变换参数 $p$ 来描述。当前扫描为一个点云 $X=x_1,...,x_n$，给定扫描点集合$X$和变换参数$p$，令空间转换函数 $T(p,x_k)$ 表示使用使用姿态变换 $p$ 来移动点 $x_k$，结合之前的一组状态密度函数（每个网格都有一个PDF），那么最好的变换参数 $p$ 应该是最大化似然函数的姿态变换：

那么最大化似然也就相当于最小化负对数似然 −logΘ;

到这里，就到了我们最熟悉的最优化的部分了。现在的任务就是使用优化算法来调整变换参数 $p$ 来最小化这个负对数似然。NDT算法使用牛顿法进行参数优化。我们不难看出，这里的概率密度函数 $f(x)$其实并不要求一定是正态分布，任何能够反映扫描表面的结构信息且对异常扫描点具有鲁棒性的概率密度函数都是可以的。

使用C++实现NDT配准

下面我们使用C++实现一个正态分布配准的例子。本例使用Point Cloud Library（PCL）提供的正态分布变换函数来对两个点云图进行配准，点云数据分别保存在 build/cloud1.pcd 和 build/cloud2.pcd 文件中。

PCL是一个用于处理2D/3D图像和点云的C++库，是一个开源项目，其github仓库：https://github.com/PointCloudLibrary/pcl 安装：http://www.pointclouds.org/downloads/

读取pcd文件中的点云信息

我们写一个函数来读取对应的pcd文件：

pcl::PointCloud::Ptr read_cloud_point(std::string const &file_path){
    // Loading first scan.
    pcl::PointCloud::Ptr cloud (new pcl::PointCloud);
    if (pcl::io::loadPCDFile (file_path, *cloud) == -1)
    {
        PCL_ERROR ("Couldn't read the pcd file\n");
        return nullptr;
    }
    return cloud;
}

在main函数中分别读取点云：

    auto target_cloud = read_cloud_point("cloud1.pcd");
    std::cout << "Loaded " << target_cloud->size () << " data points from cloud1.pcd" << std::endl;

    auto input_cloud = read_cloud_point("cloud2.pcd");
    std::cout << "Loaded " << input_cloud->size () << " data points from cloud2.pcd" << std::endl;

从两个pcd文件中读取出来的点的数量：

Loaded 112586 data points from cloud1.pcd
Loaded 112624 data points from cloud2.pcd

过滤输入点云

对如此多点做优化是非常耗时的，我们使用 voxel_filter 对输入的点云进行过滤，这里只对 input_cloud 进行了滤波处理，减少其数据量到10%左右，而target_cloud 不做滤波处理:

pcl::PointCloud::Ptr filtered_cloud (new pcl::PointCloud);
    pcl::ApproximateVoxelGrid approximate_voxel_filter;
    approximate_voxel_filter.setLeafSize(0.2, 0.2, 0.2);
    approximate_voxel_filter.setInputCloud(input_cloud);
    approximate_voxel_filter.filter(*filtered_cloud);

    std::cout<<"Filtered cloud contains "<< filtered_cloud->size() << "data points from cloud2.pcd" << 

过滤后的扫描点数量只有原来的10%

Filtered cloud contains 12433data points from cloud2.pcd

初始化NDT并且设置NDT参数，

pcl::NormalDistributionsTransform ndt;
    ndt.setTransformationEpsilon(0.01);
    ndt.setStepSize(0.1);
    ndt.setResolution(1.0);

    ndt.setMaximumIterations(35);
    ndt.setInputSource(filtered_cloud);
    ndt.setInputTarget(target_cloud);

其中 ndt.setTransformationEpsilon() 即设置变换的 ϵ（两个连续变换之间允许的最大差值），这是判断我们的优化过程是否已经收敛到最终解的阈值。ndt.setStepSize(0.1) 即设置牛顿法优化的最大步长。ndt.setResolution(1.0) 即设置网格化时立方体的边长，网格大小设置在NDT中非常重要，太大会导致精度不高，太小导致内存过高，并且只有两幅点云相差不大的情况才能匹配。ndt.setMaximumIterations(35) 即优化的迭代次数，我们这里设置为35次，即当迭代次数达到35次或者收敛到阈值时，停止优化。

初始化变换参数并开始优化

我们对变换参数 $p$ 进行初始化(给一个估计值)，虽然算法不指定初值也可以运行，但是有了它，易于得到更好的结果，尤其是当两块点云差异较大时。变换参数的初始化数据往往来自与测量数据：

Eigen::AngleAxisf init_rotation(0.6931, Eigen::Vector3f::UnitZ());
    Eigen::Translation3f init_translation (1.79387, 0.720047, 0);
    Eigen::Matrix4f init_guess = (init_translation * init_rotation).matrix();

    pcl::PointCloud::Ptr output_cloud (new pcl::PointCloud);

    ndt.align(*output_cloud, init_guess);
    std::cout << "Normal Distribution Transform has converged:" << ndt.hasConverged()
              << "score: " << ndt.getFitnessScore() << std::endl;

保存配准以后的点云图，输出到文件 cloud3.pcd ：

pcl::transformPointCloud(*input_cloud, *output_cloud, ndt.getFinalTransformation());
    pcl::io::savePCDFileASCII("cloud3.pcd", *output_cloud);

将配准以后的点云图可视化

我们写一个函数用于现实配准以后的点云,其中，目标点云（即我们已有的高精度地图）用红点绘制，而输入点云用绿点绘制：

void visualizer(pcl::PointCloud::Ptr target_cloud, pcl::PointCloud::Ptr output_cloud){
    // Initializing point cloud visualizer
    boost::shared_ptr
            viewer_final (new pcl::visualization::PCLVisualizer ("3D Viewer"));
    viewer_final->setBackgroundColor (0, 0, 0);

    // Coloring and visualizing target cloud (red).
    pcl::visualization::PointCloudColorHandlerCustom
            target_color (target_cloud, 255, 0, 0);
    viewer_final->addPointCloud (target_cloud, target_color, "target cloud");
    viewer_final->setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE,
                                                    1, "target cloud");

    // Coloring and visualizing transformed input cloud (green).
    pcl::visualization::PointCloudColorHandlerCustom
            output_color (output_cloud, 0, 255, 0);
    viewer_final->addPointCloud (output_cloud, output_color, "output cloud");
    viewer_final->setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE,
                                                    1, "output cloud");

    // Starting visualizer
    viewer_final->addCoordinateSystem (1.0, "global");
    viewer_final->initCameraParameters ();

    // Wait until visualizer window is closed.
    while (!viewer_final->wasStopped ())
    {
        viewer_final->spinOnce (100);
        boost::this_thread::sleep (boost::posix_time::microseconds (100000));
    }
}

效果：

完整代码：https://gitee.com/AdamShan/NDT_PCL_demo