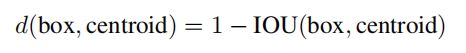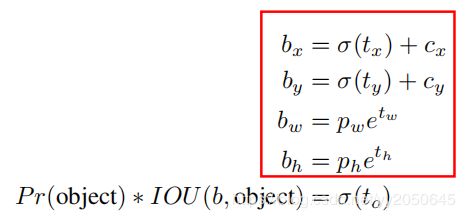YOLOV2

继YOLOV1之后，这篇文章主要讲解YOLOV2，YOLOV2可以说是在YOLOV1的基础之上采取了一系列的trick去进行改进。YOLOV2在YOLOV1的基础之上效果也有了明显的提升，接下来开始介绍YOLOV2的改进之处。

一.增加BN层

相对于YOLOV1，YOLOV2中加入了batch normalization层，加入BN层之后作者发现对于模型收敛有着明显的提升，并且发现BN层后将Dropout层去掉也并不影响预测精度，模型也并没有发生overfitting，因此BN层也可以起到正则化模型的作用。最终通过加入BN层，模型的mAP值提升了2%。

二.高像素的分类器

在YOLOV1中，使用的是在Imagenet上预训练的模型，而在Imagenet上训练使用的图像尺寸基本都小于256 * 256，但是在自己数据集训练时使用的时448 * 448的图像尺寸，这样就带来一个问题，模型不能够迅速适应当前448 * 448尺寸的图像输入。因此在YOLOV2中，首先获取Imagenet上预训练的模型，随后在448 * 448尺寸的Imagenet数据集上首先fine tune10个epoch，最后再在自己的数据集上进行fine tune，这样使得模型可以能够适应图像尺寸的转变，这个技巧使得模型提升了4%的mAP值。

三.全卷积网络与Anchor boxes

在YOLOV1中，模型最终使用了全连接层，通过对全连接层变形得到一个7 * 7 * 30的tensor作为模型输出。而在YOLO V2中取消了全连接层，整个网络采用一个全卷积的网络，那么网络输出就是一个feature map，将feature map的每一个像素当作一个anchor，一个anchor可以设置多个尺寸不同的anchor boxes，YOLOV2中仍然采用了anchor boxes去预测真实的bounding box。作者移除了之前YOLOV1中的一个池化层使得模型最终输出的feature map有着更高的像素，并且将模型输入图像尺寸由448改为了416，这是因为大部分物体都是处于图像的中间位置，而如果网络输出一个偶数尺寸的feature map，则在中心位置没有anchor，这样对于预测中间物体来说就不是那么的容易了，因此改变图像输入尺寸可以使得模型最终输出的feature map时一个奇数尺寸。YOLOV2中，整个网络相当于对图片进行了一个32倍的下采样，因此模型的输出尺寸为416 / 32 = 13，相当于有13 * 13个anchor。

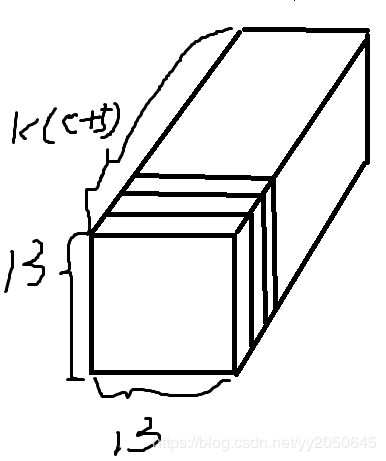
YOLOV2仍然使用YOLOV1的方式，对于每一个anchor box，除了位置信息（x, y, w, h），还要预测confidence和每个类别的条件概率prob(Class_i|object)，i=1,...,C，C为物体类别数目，这里的confidence和YOLO V1中的一致，也是prob(object) * iou，这里的prob(object)表示当前anchor box存在一个物体的概率，这里的iou是通过当前anchor box所预测得到的bounding box和ground truth bounding box的iou，因此从这里可以看出一点优于YOLOV1的就是，对于每个anchor box都会预测一个类别，那么这样就不存在YOLOV1中一个grid cell只能预测一个类别的情况，比如有3个同类物体中心落入了同一个grid cell，YOLOV1只能检测出其中的两个，或者说有2个不同类别物体中心落入了同一个grid cell则YOLOV1只能检测出其中的一个，YOLOV2对于这种情况有了很好的改善，其每个grid cell可以预测不同类别的物体，可预测数目为模型设置的每个anchor/grid cell的anchor box数目。通过上述我们可以得知，针对每个anchor box模型最终输出一个(4 + 1 + C)长度的tensor，那针对每一个anchor模型输出的是k * (4 + 1 + C)长度的tensor，k为每个anchor的anchor box数目，C为物体类别数目。因此模型最终输出的形状为(13, 13 , k * (5 + C))，通道数为k * (5 + C)，如下图所示：

采用anchor box的策略使模型的mAP值略微下降，但是召回率有了极大的提升，从81%提升至88%，并且还有一点就是，YOLOV1中一张图最多只能同时检测49 * 2=98个物体，但是YOLO V2最多可以同时检测13 * 13 * k个物体。
四.维度聚类

维度聚类是YOLOV2中的一个重要改进，其作用就是相比于原先类似于RPN网络那样人工手动先验的设置anchor boxes，这里是通过聚类的方式来得到ancbor boxes的。作者认为，类似于RPN那样的手工先验的选取anchor box当然可以，模型在训练过程中也会通过先验手选出的anchor box不断调整找到所要预测的bounding box的位置，但是如果能够一开始就设置质量较高的anchor box对于模型训练和检测来说会有更好的效果。

作者的想法使这样的，首先看一下训练集中大部分物体的ground truth bounding box都是些什么形状的，那么anchor box就设置成这些形状。具体做法如下，首先将所有训练集中的物体的bounding box的(h, w)取出，注意这里不考虑bounding box的中心坐标(x, y)的信息，那么就取出一组数据，假设训练集一共有n个bounding box，则取出的数据形状为(n, 2)，即n行两列，每一行为一个bounding box的高宽信息，也是聚类时使用的一个样本，然后对着n个样本进行kmeans聚类，具体聚多少类可自行设置，比如这里要聚5类那么就选取5个初始聚类中心(h1, w1), (h2, w2), ...(h5, w5)，之后进行kmeans聚类，注意kmeans聚类需要计算样本与样本之间的距离，一般采用欧式距离，但是这里如果使用欧式距离大的boxes会产生比小的boxes更大的误差，因此这里使用如下公式作为距离度量：

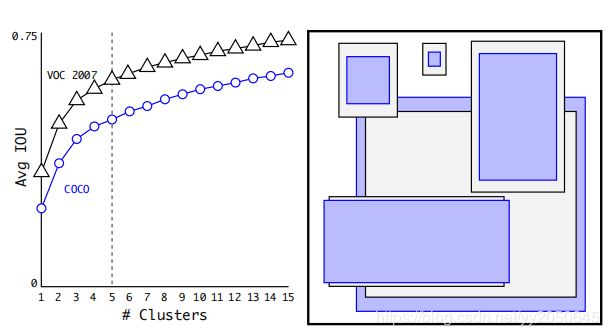
可以看出，如果boudning box和聚类中心的iou越大则说明此bounding box和聚类中心的形状越相似，则距离越小，上式的设计正好符合这种条件。然后进行聚类迭代即可得到最终的5个聚类中心，则这五个聚类中心就作为最终的anchor boxes，当然如果聚类中心更多则可以得到更多的anchor boxes。下图为作者聚类结果

可以看到，聚类中心越多则平均iou越大，这不难想象，比如前面所说共有n个样本，那如果我们聚n类，则每个样本时一个聚类中心，则平均iou为1。更多的聚类中心平局iou更大，anchor boxes形状更贴近于ground truth，模型的召回率就越高，但是模型的计算复杂度也随之上升，因此这里对于召回率和模型复杂度做了一个tradeoff，选取聚类中心数目（anchor boxes数目）为5。从上图右图中可以看到，训练集中貌似瘦高形状的bounding box更多一些。

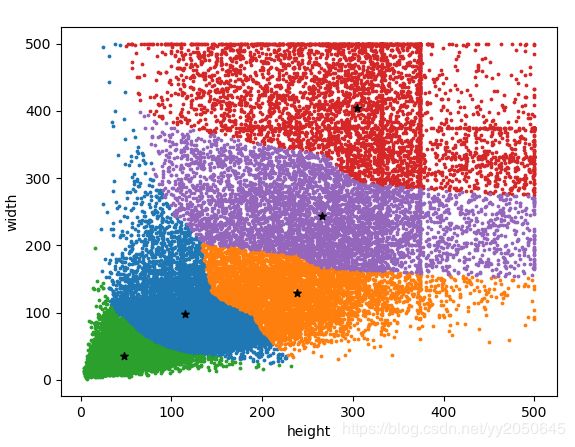
以下是我在复现yolov2时对voc 2012数据集自己划分训练集和验证集合后，对训练集的bounding box的聚类结果，这里我使用的时kmeans++，因为初始聚类中心的选取对于kmeans的聚类效果有较大的影响，如果初始点选不好则聚类效果也不好，因此这里我采用kmeans++来代替kmeans，kmeans++对于初始聚类中心的选取有更好的自适应性：

五个聚类中心(h, w)分别为: [array([114.94166885,  98.62058593]), array([237.84242061, 128.4799281 ]), array([47.17747217, 34.89194499]), array([304.95433281, 404.73914012]), array([265.41587211, 243.91430193])]

可以看到，确实瘦高的bounding box比较多。

五.直接预测位置

作者认为，类似于RPN那样的通过anchor box的中心坐标预测Bounding box的中心位置是一件糟糕的事情，其公式如下所示

注意原论文中公式写错了，右边的减号需要改为加号。tx和ty为模型输出的-1到1之间的两个数值。上式可以理解为anchor box的中心坐标加上或减去全图尺寸的一个百分比(tx, ty)作为模型预测的bounding box的中心坐标，那么作者认为这样增加了模型训练的不稳定性，因为按照这样的计算方法，预测的bounding box可以满图乱飘。

那么YOLOV2中仍然采用了YOLOV1中的方法，其只预测bounding box的中心点相对于grid cell左上角点的偏移量，因此预测bounding box的中心点不会用到anchor box的信息。

对于bounding box的预测，首先给出下图，然后对其进行解释：

如果之前聚类聚出5个簇，也就是说一个grid cell有5个anchor boxes，因此一个grid cell负责预测5个bounding box。上式中tx, ty, tw, th, to为每个anchor box都要预测的除了类别条件概率之外的5个值，也是模型的输出值，范围再负无穷到正无穷，tx, ty, tw, th代表位置信息，to代表confidence，可以看出其confidence值和YOLOV1中计算方法一致。confidence计算结果一定为0到1之间的数值，因此可以看出σ函数实际就是将数值压缩到0到1之间，可以是一个sigmoid函数。

这里的cx，cy表示的是当前grid cell相对于全图的左上角在分别在x和y方向的偏移量（注意是偏移了多少个grid cell，而不是真实的原图尺寸），例如模型输出为13 * 13的feature map，也就是将原图划分为13 * 13个grid cell，如果某一物体落入了索引为(2, 3)grid cell中（索引从0开始计算），则cy为2，cx为3。σ(tx)和σ(ty)实际得到的是0到1之间的数值，代表着在物体所落入的grid cell中，物体的中心坐标相对于这个grid cell左上角点的横向和纵向偏移量，可以理解为便宜了小数个grid cell，那么物体中心相对于全图左上角点的横向和纵向偏移量就为σ(tx) + cx，σ(ty) + cy也就是bx，by，那么就可以说物体中心点相对于左上角点横向偏移了bx个grid cell，纵向偏移了by个grid cell。最终使用bx和by分别乘以单个网格的宽和高就得到了物体在原图真实坐标。

这里bw和bh实际不用多说，和中心点预测不同，这里bw和bh得到的就是真实的宽高，而其预测使用了anchor boxes的宽高pw和ph的信息，并且预测方法和RCNN中的边框回归一样。注意tw，和th才是模型的输出，也就是模型实际预测的是log(bw / pw)以及log(bh / ph)，模型输出tw和th后通过上式就可以计算出预测的bounding box真实宽高了。

六.细粒度特征

作者认为，由于网络最终降采样32倍，得到一个13 * 13的feature map用来预测，但是这个尺寸的feature map中每一个像素的感受野都很大，因此对于大目标的检测应该不错，但是对于小物体的检测却不是那么好，因此模型的输出需要融入更细粒度的特征。那么具体做法为，在网络中添加了一个passthrough层，这个层的作用就是将网络靠前的某一层的feature map引入到最后的模型输出中，文中选取某某个卷积层，其输出为26 * 26 * 512 的feature map，那么这个feature map的感受野相对于13 * 13就小了。那怎么将其融入到最后的13 * 13的输出中去呢，其实很简单，就是沿着通道方向进行一个concatenate，那么问题来了，尺寸不一致如何进行concatenate呢？实际上文中就是将26 * 26 * 512reshape成了13 * 13 * 2048，那么这样就可以进行concatenate了。这一操作带来了1%的提升。

七.多尺度训练

因为模型是全卷积结构，因此网络能够跑通各种尺度的图像输入，因此作者就希望模型能够适应多尺度的输入，预测时能够通过不同尺度的输入来进行预测。在训练过程中图像输入尺寸不是一成不变416了，而是每10个batch进行一次转变。由于网络相当于对图像进行了32倍下采样，候选的图像尺寸必须为32的倍数，原文中采用的时{320, 352, ...., 608}这几个尺寸，网络每训练10个batch就随机选择一个图像尺寸进行训练。输入尺寸变了，输出尺寸也就随之改变，例如输入为320则输出为10 * 10尺寸，那么网络就相当于有10 * 10个anchor。

大尺寸输入，网络预测精度较高，但是网络预测速度较慢，而小尺寸的输入预测精度较低，但是速度更快，那么这样就可以根据自己的应用场景在速度和精度之间做一个tradeoff了，如果对于速度没有特别的要求，对于精度要求高那么就采用大尺度输入，否则就采用小尺度输入。

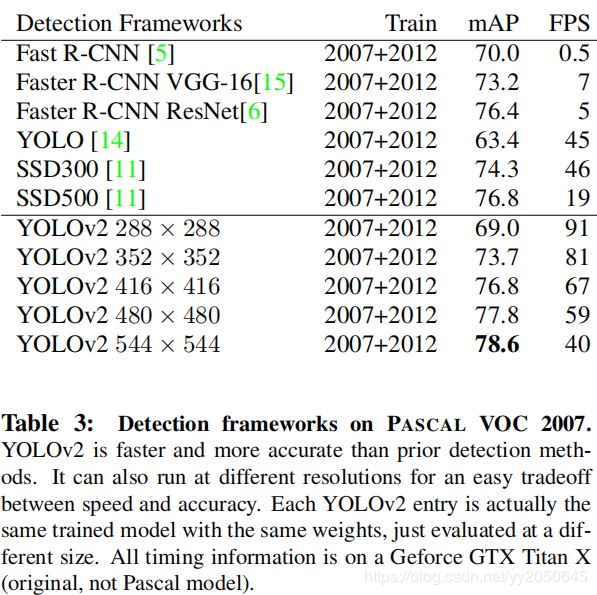
那最后看一下yolov2和其他state-of-the-art模型的对比：

可以看到，Yolov2相比与其他模型有更高的准确率以及更快的检测速度。

下图为在YOLOV1上逐步加入各个trick，mAP的变化：

可以看到YOLOV2在加上各个trick后比YOLO确实提升了很多。