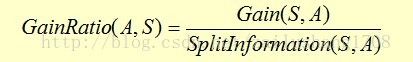对《从决策树学习谈到贝叶斯分类算法、EM、HMM》的自己总结
文章参考:《从决策树学习谈到贝叶斯分类算法、EM、HMM》
1,一个 classifier 会从它得到的训练集中进行“学习”,从而具备对未知数据进行分类的能力,这种提供训练数据的过程通常叫做 supervised learning (监督学习),监督学习属于分类算法则不准确,常见的其他监督问题,比如相似性学习,特征学习等等也是监督的,但不是分类
2,一个聚类算法通常只需要知道如何计算相似 度就可以开始工作了,因此 clustering 通常并不需要使用训练数据进行学习,这在 Machine Learning 中被称作 unsupervised learning (无监督学习).
3,当样例是输入/输出对给出时,称为监督学习,有关输入/输出函数关系的样例称为训练数据。而在无监督学习中,其数据不包含输出值,学习的任务是理解数据产生的过程。
4,决策树的举例:①决策树分类的思想类似于找对象 ②天气的情况决定是否打球。。
5,决策树算法
步骤:
自上而下分而治之的方法
开始时,所有的数据都在根节点
所有记录用所选属性递归的进行分割
属性的选择是基于一个启发式规则或者一个统计的度量 (如, information gain)
停止分割的条件:
一个节点上的数据都是属于同一个类别
没有属性可以再用于对数据进行分割
建树阶段
MakeTree (Training Data T)
Partition (T);
Partition (Data S)
if (all points in S are in the same class or no attributes)
then return;
else
evaluate splits for each attribute A
Use best split found to partition S into S1 and S2;
Partition (S1);
Partition (S2);
6,C++中的向量解释:
vector<int> count (2,0); 表示创建一个向量(相当于一位数组),它有2个元素,且它的每一个值都是0,以后就可以用count【i】
vector
7,ID3算法的核心思想:就是以信息增益度量属性选择
熵:它刻画了任意样例集的纯度,熵越大表明样本集越不纯。比如:S的所有成员属于同一类,Entropy(S)=0; S的正反样例数量相等,Entropy(S)=1;
步骤:
①计算数据集S的熵 E(S)=-∑Pi log2(pi) (i=1,…,m)其中ii表示种类,pi表示种类比例。
②计算每一个属性的信息熵:E(A)= ∑(|si|/|s| * E(si)) (S划分为v个子集{S1,S2,…si....,Sv}), E(si)表示子集的熵
③Gain(S,A)= E(s) - E(A):计算属性A的信息增益(越大表明越先选择该属性为分支)
代码:
function ID3 (R: 一个非类别属性集, C: 类别属性, S: 一个训练集)
returns 一棵决策树;
begin
If S为空
return 一个值为Failure的节点;
If S由纯粹是相同种类属性值的记录构成
return 一个该值构成的节点;
If R为空
return 一个节点,值为S中所有记录的类别属性中最频繁出现的值;
//有的记录被不正确的分类,所以这里会出现错误
D = R中Gain(D,S)最高的属性;
{dj| j=1,2, .., m} = D的属性值;
{Sj| j=1,2, .., m} = S的子集,Sj的所有记录的属性D的值为dj
返回一棵树,根节点标记为D,弧标记为d1, d2, .., dm,弧对应的子树分别为
ID3(R-{D}, C, S1), ID3(R-{D}, C, S2), .., ID3(R-{D}, C, Sm);
end ID3;
id3局限:
①信息增益度量存在一个内在偏置,它偏袒具有较多值的属性。例如,如果有一个属性为日期,那么将有大量取值,这个属性可能会有非常高的信息增益。假如它被选作树的根结点的决策属性则可能形成一颗非常宽的树,这棵树可以理想地分类训练数据,但是对于测试数据的分类性能可能会相当差。
②ID3算法增长树的每一个分支的深度,直到属性的使用无法导致信息增益。当数据中有噪声或训练样例的数量太少时,产生的树会过渡拟合训练样例。
8,C4.5算法
C4.5算法是ID3的改进算法,那么C4.5相比于ID3改进的地方有哪些呢?
有以下改进:
a.用增益比率的概念(通过增加分母分割信息,解决了ID3偏袒具有较多值的属性的缺点);
分割信息:(分割信息是S关于属性A的各值的熵,如果属性值比较多,并且样本分布比较离散,那么该属性的分割信息就会大,导致最后的信息增益率降低,这也解决了ID3偏袒具有较多值的属性的缺点)
增益比率:
其中:G(S,A)和上面ID3的一样。。。
增益比率最大属性就是最优的属性
b.合并连续值属性;
c.可以处理缺少属性值的训练样本;
d.通过使用不同的修剪技术以避免树的不平衡;
e.K次迭代交叉验证;
f.规则的产生。
最后总结:
- 实际应用中,决策树overfitting比较的严重,一般要做boosting。
- 分类器的性能上不去,很主要的原因在于特征的鉴别性不足,而不是分类器的好坏,好的特征才有好的分类效果,分类器只是弱相关。 那如何提高 特征的鉴别性呢?一是设计特征时尽量引入domain knowledge,二是对提取出来的特征做选择、变换和再学习,这一点是机器学习算法不管的部分。。。
第二部分、贝叶斯分类
1,Bayes定理可表述为:后验概率 = 标准相似度*先验概率
P(A/B) 表示A的后验概率,P(A)表示A的先验概率
其中 比例 P(B|A)/P(B) 被称作标准相似度(0-1之间,它越小表明A和B相互影响比较大)
2个例子来理解贝叶斯:
例1:键盘敲入一个错误的单词后,系统如何判断他想敲入的是什么单词呢?比如敲入thew后系统判断是想敲入the呢?还是thaw呢?
p(the/thew)正比于p(the)*p(thew/the) :用户实际是想输入 the 的可能性大小取决于 the 本身在词汇表中被使用的可能性(频繁程度)大小(先验概率)和 想打 the 却打成 thew 的可能性大小(似然)的乘积。
例2:学校里男生(60%),女生(40%),男生都穿长裤(100%),女生一般穿短裤(50%),一般穿长裤(50%),然后来了一群穿长裤的人(不知道性别),请你判断女生的人数。。。
解:其实就是计算P(Girl|Pants) = P(Pants, Girl)/P(Pants) (这和学习总人数无关)
3贝叶斯的应用
①中文分词:给你一个句子,如何分割成单词呢?设句子为X,分割方法为Y
那么P(Y|X) ∝ P(Y)*P(X|Y) (显然P(X|Y)为1,因为分割法确定后把分割符去掉就是这个句子)
所以P(Y|X) ∝ P(Y) 。也就是寻找一种分词使得这个词串(句子)的概率最大化。
而如何计算一个词串W1, W2, W3, W4 ..的可能性呢?
我们假设句子中一个词的出现概率只依赖于它前面的有限的 k 个词(k 一般不超过 3,如果只依赖于前面的一个词,就是2元语言模型(2-gram),同理有 3-gram 、 4-gram 等),这个就是所谓的“有限地平线”假设。
那么一种分割方法可表示为P(W1, W2, W3, W4 ..) =P(W1) * P(W2|W1) * P(W3|W2) * P(W4|W3) ,计算所以分割方式取概率最大的分割方法
以如何分割句子”南京市长江大桥“为例
p(南京市长,江大桥)=0的(因为在语料库中单词南京市长和江大桥同时出现概率为0)
p(南京市 ,长江大桥)的概率是最高的,那么就选择这种分割方法了!!!
总结:总的来说很多问题还是依赖于大数据的,比如此例中依赖语料库这个大数据库,所以说大数据是未来的方向。。。
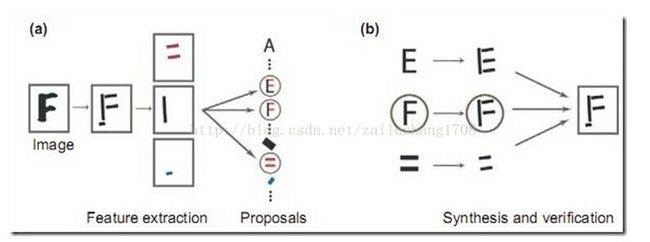
②贝叶斯图像识别,Analysis by Synthesis
首先是视觉系统提取图形的边角特征,然后使用这些特征自底向上地激活高层的抽象概念(比如是 E 还是 F 还是等号),然后使用一个自顶向下的验证来比较到底哪个概念最佳地解释了观察到的图像。
③最大似然与最小二乘
回归可以看作是拟合的特例,即允许误差的拟合
下面解释用贝叶斯解释最小二乘法:
P(h|D) ∝ P(h) * P(D|h)
这里 h 就是指一条特定的直线,D 就是指这 N 个数据点。我们需要寻找一条直线 h 使得 P(h) * P(D|h) 最大。
很显然,P(h) 这个先验概率是均匀的,因为哪条直线也不比另一条更优越。所以我们只需要看 P(D|h) 这一项,这一项是指这条直线生成这些数据点的概率,刚才说过了,生成数据点 (Xi, Yi) 的概率为 EXP[-(ΔYi)^2] 乘以一个常数。而 P(D|h) = P(d1|h) * P(d2|h) * .. 即假设各个数据点是独立生成的,所以可以把每个概率乘起来。于是生成 N 个数据点的概率为 EXP[-(ΔY1)^2] * EXP[-(ΔY2)^2] * EXP[-(ΔY3)^2] * .. = EXP{-[(ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + ..]} 最大化这个概率就是要最小化 (ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + .. 。 得证
第三部分 朴素贝叶斯方法
在众多的分类模型中,应用最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型(Naive Bayesian Model,NBC)
在属性个数比较多或者属性之间相关性较大时,NBC模型的分类效率比不上决策树模型。而在属性相关性较小时,NBC模型的性能最为良好。