上采样之双线性插值法
上采样之双线性插值法
- One:上采样的定义
- 上采样的类型:
- 一、双线性插值:
- 二、转置卷积 :
- 三、上采样(unsampling)
- 四、上池化(unpooling)
- 总结:
- tow:具体的讲解双线性插值
- 线性插值
- 具体来说线性插值的过程如下:(如图:)
- 扩展到双线性插值:
- Three:Python实现
One:上采样的定义
上采样实际上是一个统称。在下采样的过程中,我们把一张图片的特征提取出来,实际上是把图片的关键部分提取出来的,图片的分辨率就降低了,可以说图片缩小了;在上采样过程中,要恢复图片的大小,提高图片的分辨率,就要用到一些方法,任何可以让图片变成高分辨率的技术都可以称为上采样。
上采样的类型:
1. 双线性插值
双线性插值又称为双线性内插
2. 转置卷积
转置卷积又称为反卷积,但是这种叫法是不对的。
3. 上采样—Unsampling
4. 上池化—Unpooling
一、双线性插值:
FCN(全卷机神经网络)中上采样的过程用到的就是双线性插值法,双线性插值不需要学习任何的参数,通过人为的操作的。
实际上,双线性插值还包括:{最近邻插值、双线性插值、双立方插值},后面我们会详细的讲解第二种——双线性插值。
二、转置卷积 :
有人称转置卷积为** 反卷积**,这种叫法是不对的,以后不要这样叫了。
双线性插值不需要学习参数,但是转置卷积最大的特点就是要学习参数。
三、上采样(unsampling)
上采样(unsampling)相对来说比较简单,直接填充最临近的数值:

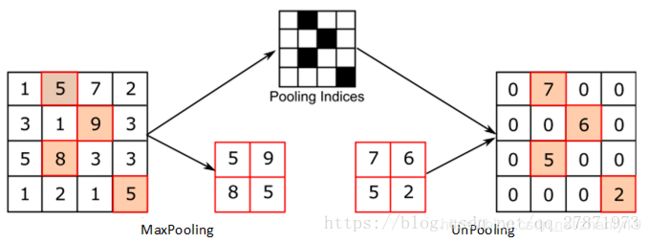
四、上池化(unpooling)
上池化,又称为** 反池化 **,这个过程中保存了最大池化的位置,应该将上池化和下采样结合起来。
总结:
对比上面两个示意图,可以发现区别:
两者的区别在于UnSampling阶段** 没有 **使用MaxPooling时的位置信息,而是直接将内容复制来扩充Feature Map。第一幅图中右边4*4矩阵,用了四种颜色的正方形框分割为四个区域,每一个区域内的内容是直接复制上采样前的对应信息。UnPooling的过程,特点是在Maxpooling的时候保留最大值的位置信息,之后在unPooling阶段使用该信息扩充Feature Map,除最大值位置以外,其余补0。
tow:具体的讲解双线性插值
在讲解双线性插值的时候,先讲解线性插值:
线性插值
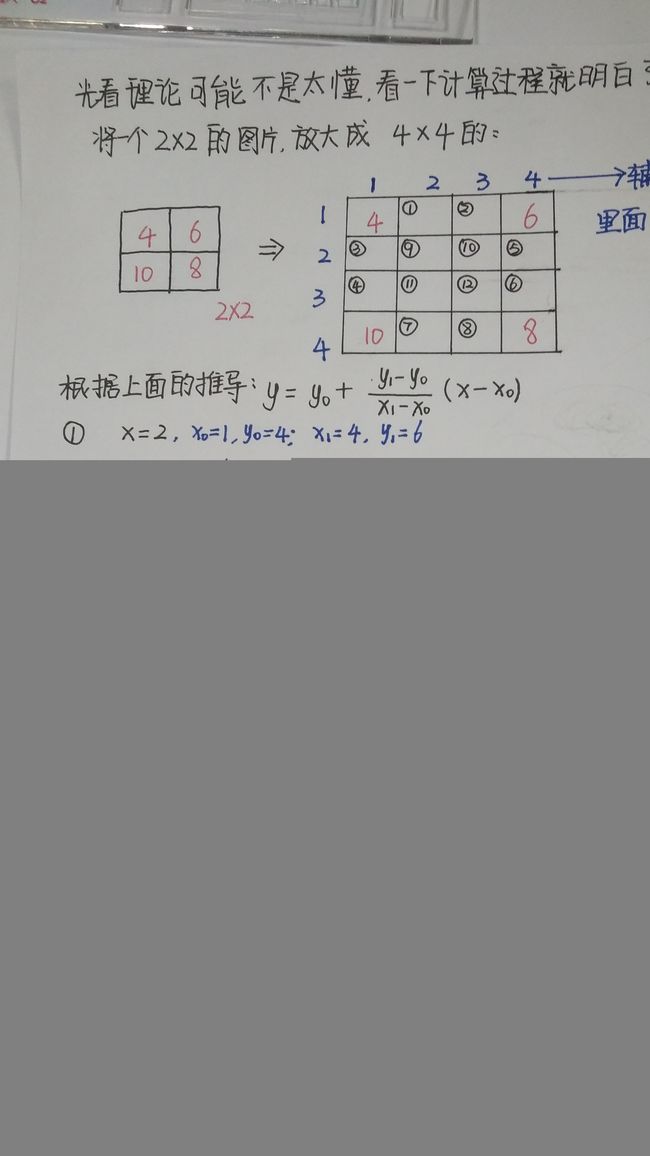
我们想把一个像素为2 * 2的图片放大为一个3 * 3 的图片,如下图所示:
 上图中,我们已经知道的是四个值,为了放大图片,我们进行根据已知的像素点填充未知的像素点
上图中,我们已经知道的是四个值,为了放大图片,我们进行根据已知的像素点填充未知的像素点
特别注意:线性插值是一种针对一维数据的插值方法,它根据一维数据序列中需要插值的点的左右邻近两个数据点来进行数值的估计,根据到这两个点的距离来分配它们的比重的。
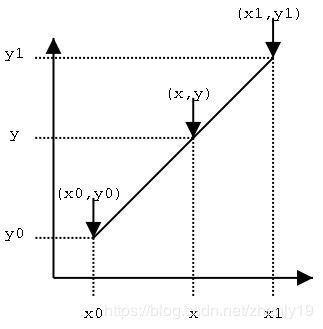
具体来说线性插值的过程如下:(如图:)
根据图中的假设:已知点(x0,y0)、(x1,y1),试问在x处插值,y的值是多少?用我们初中学过的知识,已知两个点的坐标可以得到一条线,又已知线上一点的一个坐标可以求得这个点的另一个坐标值。这就是线性插值的原理。x只是表示的相对的位置,y才是我们想要的结果:

详细过程以及结果:

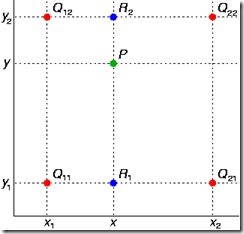
扩展到双线性插值:
如图,已知Q12,Q22,Q11,Q21,但是要插值的点为P点,这就要用双线性插值了,首先在x轴方向上,对R1和R2两个点进行插值,这个很简单,然后根据R1和R2对P点进行插值,这就是所谓的双线性插值。
Three:Python实现
import cv2
import numpy as np
import time
def resize(src, new_size):
dst_w, dst_h = new_size # 目标图像宽高
src_h, src_w = src.shape[:2] # 源图像宽高
if src_h == dst_h and src_w == dst_w:
return src.copy()
scale_x = float(src_w) / dst_w # x缩放比例
scale_y = float(src_h) / dst_h # y缩放比例
# 遍历目标图像,插值
dst = np.zeros((dst_h, dst_w, 3), dtype=np.uint8)
for n in range(3): # 对channel循环
for dst_y in range(dst_h): # 对height循环
for dst_x in range(dst_w): # 对width循环
# 目标在源上的坐标
src_x = (dst_x + 0.5) * scale_x - 0.5
src_y = (dst_y + 0.5) * scale_y - 0.5
# 计算在源图上四个近邻点的位置
src_x_0 = int(np.floor(src_x))
src_y_0 = int(np.floor(src_y))
src_x_1 = min(src_x_0 + 1, src_w - 1)
src_y_1 = min(src_y_0 + 1, src_h - 1)
# 双线性插值
value0 = (src_x_1 - src_x) * src[src_y_0, src_x_0, n] + (src_x - src_x_0) * src[src_y_0, src_x_1, n]
value1 = (src_x_1 - src_x) * src[src_y_1, src_x_0, n] + (src_x - src_x_0) * src[src_y_1, src_x_1, n]
dst[dst_y, dst_x, n] = int((src_y_1 - src_y) * value0 + (src_y - src_y_0) * value1)
return dst
if __name__ == '__main__':
img_in = cv2.imread('../data/picture/timg.jpg')
start = time.time()
img_out = cv2.resize(img_in, (600,600))
#print'cost %f seconds' % (time.time() - start)
cv2.imshow('src_image', img_in)
cv2.imshow('dst_image', img_out)
cv2.waitKey()
双线性插值是图像缩放的一种方式,其主要分为两步线性插值,一是在x方向插值,二是用x方向插值结果再在y方向插值,具体步骤如下:
1.定位像素点
先找到目标图像像素点(dst_x, dst_y)在源图像上的像素点位置(src_x, src_y)。
一般是使用直接缩放:
src_x=dst_x * scale_x (scale_x为源图像与目标图像宽比例)
而我们这里使用几何中心对称:
src_x = (dst_x + 0.5) * scale_x - 0.5
然后找到上下左右最近邻的四个像素点用于计算插值。
2. 两步插值(借别人图)

效果图如下: