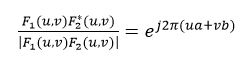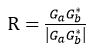Opencv2.4.9源码分析——phaseCorrelate
相位相关法(phase correlate)可以用于检测两幅内容相同的图像之间的相对位移量。它是基于傅立叶变换的位移定理:一个平移过的函数的傅立叶变换仅仅是未平移函数的傅立叶变换与一个具有线性相位的指数因子的乘积,即空间域中的平移会造成频域中频谱的相移。它的公式定义为:设二维函数(图像)f(x,y)的傅立叶变换为F(u,v),即DFT[f(x,y)]=F(u,v),如果f(x,y)平移(a,b),则平移后的傅立叶变换为:
因此,当两幅函数f1(x,y)和f2(x,y)仅仅有位移的差异,即f2(x,y)= f1(x-a,y-b),则它们的傅立叶变换F1(u,v)和F2(u,v)有如下关系:
![]() (2)
(2)
由上式很容易得到f1(x,y)和f2(x,y)的互功率谱为(这里还用到了f1(x,y)和f2(x,y)的频谱的模相等):
式中F*表示F的共轭,上式表示平移定理保证了互功率谱的相位等于两幅图像之间的相移。
Opencv的文档给出了详细的用相位相关法求解位移量的过程,
1、对待处理的两幅图像src1和src2应用窗函数去除图像的边界效应,文档中推荐使用汉宁窗,它可用createHanningWindow函数生成;
2、求傅立叶变换:Ga=DFT[scr1]和Ga=DFT[scr1];
4、对互功率谱求傅立叶逆变换:r=DFT-1[R];
5、对r计算最大值的位置,并在以该位置为中心的5×5的窗体内应用下列公式获得亚像素级的精度位置:
最终(a,b)为两个图像之间的位移量。
phaseCorrelate函数的原型为:
Point2d phaseCorrelate(InputArray src1,InputArray src2, InputArray window=noArray())
src1和src2为两个要比较的图像,window为步骤1中所要用到的窗函数,该参数可选,默认情况下不使用任何窗函数,函数返回是具有亚像素级精度的位移量。
下面就给出具体的源码分析,该函数在source/modules/imgproc/src/phasecorr.cpp文件内,cv::Point2d cv::phaseCorrelate(InputArray _src1, InputArray _src2, InputArray _window)
{
return phaseCorrelateRes(_src1, _src2, _window, 0);
}
phaseCorrelateRes函数的第4个参数表示的是最大响应值,也就是公式4中分母部分的归一化后的值,在这里我们没有用到它。
cv::Point2d cv::phaseCorrelateRes(InputArray _src1, InputArray _src2, InputArray _window, double* response)
{
//分别得到两幅输入图像和窗函数的矩阵形式
Mat src1 = _src1.getMat();
Mat src2 = _src2.getMat();
Mat window = _window.getMat();
//输入图像的类型和大小的判断,必须一致,而且类型必须是32位或64位浮点灰度图像
CV_Assert( src1.type() == src2.type());
CV_Assert( src1.type() == CV_32FC1 || src1.type() == CV_64FC1 );
CV_Assert( src1.size == src2.size);
//如果使用窗函数,则窗函数的大小和类型必须与输入图像的一致
if(!window.empty())
{
CV_Assert( src1.type() == window.type());
CV_Assert( src1.size == window.size);
}
//因为要进行离散傅立叶变换,所以为了提高效率,就要得到最佳的图像尺寸
int M = getOptimalDFTSize(src1.rows);
int N = getOptimalDFTSize(src1.cols);
Mat padded1, padded2, paddedWin;
//生成尺寸修改以后的矩阵
if(M != src1.rows || N != src1.cols) //最佳尺寸不是原图像的尺寸
{
//通过补零的方式填充多出来的像素
copyMakeBorder(src1, padded1, 0, M - src1.rows, 0, N - src1.cols, BORDER_CONSTANT, Scalar::all(0));
copyMakeBorder(src2, padded2, 0, M - src2.rows, 0, N - src2.cols, BORDER_CONSTANT, Scalar::all(0));
if(!window.empty())
{
copyMakeBorder(window, paddedWin, 0, M - window.rows, 0, N - window.cols, BORDER_CONSTANT, Scalar::all(0));
}
}
else //最佳尺寸与原图像的尺寸一致
{
padded1 = src1;
padded2 = src2;
paddedWin = window;
}
Mat FFT1, FFT2, P, Pm, C;
// perform window multiplication if available
//执行步骤1,两幅输入图像分别与窗函数逐点相乘
if(!paddedWin.empty())
{
// apply window to both images before proceeding...
multiply(paddedWin, padded1, padded1);
multiply(paddedWin, padded2, padded2);
}
// execute phase correlation equation
// Reference: http://en.wikipedia.org/wiki/Phase_correlation
//执行步骤2,分别对两幅图像取傅立叶变换
dft(padded1, FFT1, DFT_REAL_OUTPUT);
dft(padded2, FFT2, DFT_REAL_OUTPUT);
//执行步骤3
//计算互功率谱的分子部分,即公式3中的分子,其中P为输出结果,true表示的是对FF2取共轭,所以得到的结果为:P=FFT1×FFT2*,mulSpectrums函数为通用函数
mulSpectrums(FFT1, FFT2, P, 0, true);
//计算互功率谱的分母部分,即公式3中的分母,结果为:Pm=|P|,magSpectrums函数就是在phasecorr.cpp文件内给出的,它的作用是对复数取模。
magSpectrums(P, Pm);
//计算互功率谱,即公式3,结果为:C=P / Pm,divSpectrums函数也是在phasecorr.cpp文件内给出的,它仿照mulSpectrums函数的写法,其中参数false表示不取共轭
divSpectrums(P, Pm, C, 0, false); // FF* / |FF*| (phase correlation equation completed here...)
//执行步骤4,傅立叶逆变换
idft(C, C); // gives us the nice peak shift location...
/*平移处理,fftShift函数也是在phasecorr.cpp文件内给出的,它的作用是把图像平均分割成——左上、左下、右上、右下,把左上和右下对调,把右上和左下对调。它的目的是把能量调整到图像的中心,也就是图像的中心对应于两幅图像相频差为零的地方,即没有发生位移的地方。*/
fftShift(C); // shift the energy to the center of the frame.
//执行步骤5
// locate the highest peak
//找到最大点处的像素位置,minMaxLoc为通用函数
Point peakLoc;
minMaxLoc(C, NULL, NULL, NULL, &peakLoc);
// get the phase shift with sub-pixel accuracy, 5x5 window seems about right here...
//在5×5的窗体内确定亚像素精度的坐标位置
Point2d t;
// weightedCentroid也是在phasecorr.cpp文件内给出的,它是利用公式4来计算更精确的坐标位置
t = weightedCentroid(C, peakLoc, Size(5, 5), response);
// max response is M*N (not exactly, might be slightly larger due to rounding errors)
//求最大响应值
if(response)
*response /= M*N;
// adjust shift relative to image center...
//最终确定位移量
//先找到图像中点,然后用中点减去由步骤5得到的坐标位置
Point2d center((double)padded1.cols / 2.0, (double)padded1.rows / 2.0);
return (center - t);
}
phaseCorrelate函数的源码可读性较强,而且它的原理在文档中说明得也十分清晰,因此对相位相关的理解难度应该不大。下面就给出具体的实现程序。我是对彩色图像进行测试,因为phaseCorrelate函数只能处理32位或64位浮点型的单通道图像,因此如果不是处理这类图像,是需要进行转换的。
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include
using namespace cv;
using namespace std;
int main( int argc, char** argv )
{
Mat src1, src2;
Mat dst1, dst2;
if( argc != 3 || !(src1=imread(argv[1], 1)).data || !(src2=imread(argv[2], 1)).data)
return -1;
cvtColor( src1, src1, CV_BGR2GRAY ); //转换为灰度图像
src1.convertTo(dst1,CV_32FC1); //转换为32位浮点型
cvtColor( src2, src2, CV_BGR2GRAY );
src2.convertTo(dst2,CV_32FC1);
Point2d phase_shift;
phase_shift = phaseCorrelate(dst1,dst2);
cout<
最终得到的结果是:
warp:
X shift : 3.803 Y shift : 21.8661