Policy Gradient(PG算法)理解笔记
学习PG算法,看了很多的文章,看代码也花了不少时间,这篇文章主要写莫烦老师给的程序的理解,当然也结合了一些文章里面的公式推导,还参考了其他相关的文章
代码
这边直接给出莫烦老师的RL代码,其他剩余的理解不难,可以自己下载。
import numpy as np
import tensorflow as tf
# reproducible
np.random.seed(1)
tf.set_random_seed(1)
class PolicyGradient:
def __init__(
self,
n_actions,
n_features,
learning_rate=0.01,
reward_decay=0.95,
output_graph=False,
):
self.n_actions = n_actions
self.n_features = n_features
self.lr = learning_rate
self.gamma = reward_decay
self.ep_obs, self.ep_as, self.ep_rs = [], [], []
self._build_net()
self.sess = tf.Session()
if output_graph:
# $ tensorboard --logdir=logs
# http://0.0.0.0:6006/
# tf.train.SummaryWriter soon be deprecated, use following
tf.summary.FileWriter("logs/", self.sess.graph)
self.sess.run(tf.global_variables_initializer())
def _build_net(self):
with tf.name_scope('inputs'):
self.tf_obs = tf.placeholder(tf.float32, [None, self.n_features], name="observations")
self.tf_acts = tf.placeholder(tf.int32, [None, ], name="actions_num")
self.tf_vt = tf.placeholder(tf.float32, [None, ], name="actions_value")
# fc1
layer = tf.layers.dense(
inputs=self.tf_obs,
units=10,
activation=tf.nn.tanh, # tanh activation
kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.3),
bias_initializer=tf.constant_initializer(0.1),
name='fc1'
)
# fc2
all_act = tf.layers.dense(
inputs=layer,
units=self.n_actions,
activation=None,
kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.3),
bias_initializer=tf.constant_initializer(0.1),
name='fc2'
)
self.all_act_prob = tf.nn.softmax(all_act, name='act_prob') # use softmax to convert to probability
with tf.name_scope('loss'):
# to maximize total reward (log_p * R) is to minimize -(log_p * R), and the tf only have minimize(loss)
neg_log_prob = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=all_act, labels=self.tf_acts) # this is negative log of chosen action
# or in this way:
# neg_log_prob = tf.reduce_sum(-tf.log(self.all_act_prob)*tf.one_hot(self.tf_acts, self.n_actions), axis=1)
loss = tf.reduce_mean(neg_log_prob * self.tf_vt) # reward guided loss
with tf.name_scope('train'):
self.train_op = tf.train.AdamOptimizer(self.lr).minimize(loss)
def choose_action(self, observation):
prob_weights = self.sess.run(self.all_act_prob, feed_dict={self.tf_obs: observation[np.newaxis, :]})
action = np.random.choice(range(prob_weights.shape[1]), p=prob_weights.ravel()) # select action w.r.t the actions prob
return action
def store_transition(self, s, a, r):
self.ep_obs.append(s)
self.ep_as.append(a)
self.ep_rs.append(r)
def learn(self):
# discount and normalize episode reward
discounted_ep_rs_norm = self._discount_and_norm_rewards()
# train on episode
self.sess.run(self.train_op, feed_dict={
self.tf_obs: np.vstack(self.ep_obs), # shape=[None, n_obs]
self.tf_acts: np.array(self.ep_as), # shape=[None, ]
self.tf_vt: discounted_ep_rs_norm, # shape=[None, ]
})
self.ep_obs, self.ep_as, self.ep_rs = [], [], [] # empty episode data
return discounted_ep_rs_norm
def _discount_and_norm_rewards(self):
# discount episode rewards
discounted_ep_rs = np.zeros_like(self.ep_rs)
running_add = 0
for t in reversed(range(0, len(self.ep_rs))):
running_add = running_add * self.gamma + self.ep_rs[t]
discounted_ep_rs[t] = running_add
# normalize episode rewards
discounted_ep_rs -= np.mean(discounted_ep_rs)
discounted_ep_rs /= np.std(discounted_ep_rs)
return discounted_ep_rs
理解
with tf.name_scope('loss'):
# to maximize total reward (log_p * R) is to minimize -(log_p * R), and the tf only have minimize(loss)
neg_log_prob = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=all_act, labels=self.tf_acts) # this is negative log of chosen action
# or in this way:
# neg_log_prob=tf.reduce_sum(-tf.log(self.all_act_prob)*tf.one_hot(self.tf_acts, self.n_actions), axis=1)
loss = tf.reduce_mean(neg_log_prob * self.tf_vt) # reward guided loss
with tf.name_scope('train'):
self.train_op = tf.train.AdamOptimizer(self.lr).minimize(loss)
tf.nn.sparse_softmax_cross_entropy_with_logits这行代码作用是和下面注释掉的计算结果是一样的,如图所示:
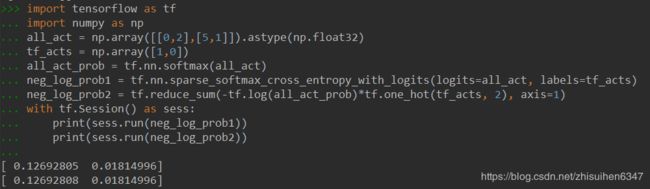
还有tf.log(self.all_act_prob)*tf.one_hot(self.tf_acts, self.n_actions),两个矩阵相乘是Hadamard积,我们普通用的矩阵相乘在tensorflow中应该写成:tf.matmul()。至于tf.one_hot函数的效果如图:
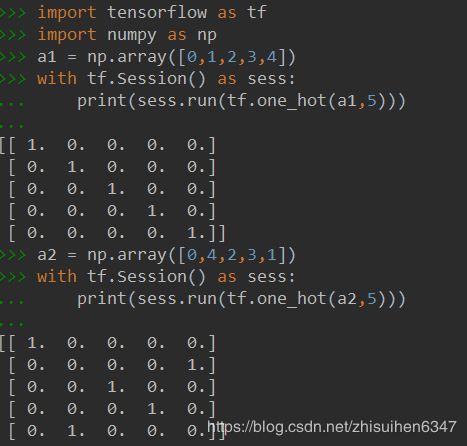
作用就是把执行的动作化为一个矩阵,比如上面的a2,第一位0,那矩阵的第一行第一位为1,第二位为4,那矩阵的第二行第5位为1,以此类推。
接下来,也是我学习的时候最头疼的地方: P G 算 法 是 基 于 P o l i c y 的 算 法 , 目 标 应 该 是 最 大 化 价 值 函 数 , 为 什 么 程 序 里 面 实 现 的 时 候 是 最 小 化 损 失 函 数 呢 ? \color{#ea4335}{PG算法是基于Policy的算法,目标应该是最大化价值函数,为什么程序里面实现的时候是最小化损失函数呢?} PG算法是基于Policy的算法,目标应该是最大化价值函数,为什么程序里面实现的时候是最小化损失函数呢?
下面是我自己的理解,如果错了,欢迎指正讨论。
首先参考这篇文章里面有公式额推导,如下图:
我蓝色画来的两个公式相等,考虑到这是对 θ \theta θ的求导,那么我们所要最大化的 R ˉ θ \bar{R}_\theta Rˉθ是不是可以理解为等于 1 N ∑ n = 1 N R ( τ n ) log p θ ( τ n ) \frac{1}{N}\sum_{n=1}^NR(\tau_n)\log p_\theta (\tau^n) N1∑n=1NR(τn)logpθ(τn),因为程序里面实现的时候是每个episode更新一下神经网络的,所以前面的 1 N ∑ n = 1 N \frac{1}{N}\sum_{n=1}^N N1∑n=1N可以省略,最后程序里面最大化的目标就是 R ( τ n ) log p θ ( τ n ) R(\tau_n)\log p_\theta (\tau^n) R(τn)logpθ(τn),我们求得时候是求得 − log ( ) -\log() −log(),所以最终的结果是要去最小化loss函数的。
之后的_discount_and_norm_rewards函数也很好理解,就是奖励的累加啦,然后标准化一下,同意可以参考上面那篇公式推导的文章。