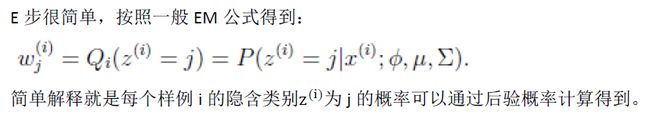混合高斯的EM算法的R代码及疑问

第一次写博客，好紧张

学习了EM的理论后想写一下练练手。在网上找到了混合高斯的R代码；但是这个代码是有问题的，它只能在某些特定情况下使用。

模拟数据是样本集5000个，前2000个是以3为均值，1为方差的高斯分布，后3000个是以-2为均值，2为方差的高斯分布。

# 模拟数据
miu1 <- 3
miu2 <- -2
sigma1 <- 1
sigma2 <- 2
alpha1 <- 0.4
alpha2 <- 0.6
# 生成两种高斯分布的样本
n <- 5000
x <- rep(0,n)
n1 <- floor(n*alpha1)
n2 <- n - n1
x[1:n1] <- rnorm(n1)*sigma1 + miu1
x[(n1+1):n] <- rnorm(n2)*sigma2 + miu2
hist(x,freq=F)
lines(density(x),col='red')
# 设置初始值
m <- 2
miu <- runif(m)
sigma <- runif(m)
alpha <- c(0.2,0.8)
prob <- matrix(rep(0,n*m),ncol=m)
# 迭代
for (step in 1:100){
# E步，已知参数求概率
for (j in 1:m){
        prob[,j]<- sapply(x,dnorm,miu[j],sigma[j])
    }
    sumprob <- rowSums(prob)
    prob<- prob/sumprob     ####求出样本属于各类的概率


    oldmiu <- miu
    oldsigma <- sigma
    oldalpha <- alpha


## M步 更新参数
 for (j in 1:m){
        p1 <- sum(prob[ ,j])
        p2 <- sum(prob[ ,j]*x)
        miu[j] <- p2/p1
        alpha[j] <- p1/n
        p3 <- sum(prob[ ,j]*(x-miu[j])^2)
        sigma[j] <- sqrt(p3/p1)
    }


## 结束迭代的条件
epsilo <- 1e-4
    if (sum(abs(miu-oldmiu))

有疑问的是在E步里面求样本属于各个类的概率的步骤，上面给出的代码是用P(Xi|z=j)/∑P(xi|zj)计算。但是在看理论的时候E步计算的应该是P(z=j|xi)，也就是z=j的后验概率。

用贝叶斯公式，后验概率可以从先验概率计算得到。（这玩意怎么编辑公式？只能截图了）

其中P(x|z)是高斯分布的概率密度，P(z)就是代码中的alpha。

于是我修改了一下上面代码中E步的prob参数计算的方法：

for (j in 1:m){
   prob[,j]<- sapply(x,dnorm,miu[j],sigma[j])
}

for(i in (1:dim(prob)[1])){
   px<-alpha%*%prob[i,]
   prob[i,]<-(prob[i,]*alpha)/px
}

这样计算的prob才是z=j的后验概率。分别贴出来修改前后的计算结果：

修改前：step 35 miu 2.843996 -2.195416 sigma 1.097323 1.849515 alpha 0.4422249 0.5577751 

到第35次迭代时收敛，得到的均值是2.843996，-2.195416 （真实值是3，-2），方差1.097323，1.849515（真实值是1，2），alpha 0.4422249，0.5577751 （真实值0.4,0.6）。

修改后的：step 57 miu -1.924697 3.005561 sigma 2.038401 0.9782731 alpha 0.6028941 0.3971059 

到第57次迭代时收敛，得到的均值是3.005561，-1.924697 （真实值是3，-2），方差0.9782731，2.0384（真实值是1，2），alpha 0.3971，0.6029 （真实值0.4,0.6）。

显然修改后的参数估计更接近实际值。其实如果alpha=（0.5,0.5）的话，修改后的计算公式就是等于修改前的。也就是说，如果每个类别的样本数相差不大的话，修改前的计算结果应该是接近修改后的，反之则不然。好了，下面开始喜闻乐见的实验时间。之前模拟数据一组是2000，一组3000个。两者相差不大，现在吧数量差距加大，一个1000，一个4000。为了使数据分得开，把sigma2调小了一点。

miu1 <- 3
miu2 <- -2
sigma1 <- 1
sigma2 <- 1.5
alpha1 <- 0.2
alpha2 <- 0.8
# 生成两种高斯分布的样本
n <- 5000
x <- rep(0,n)
n1 <- floor(n*alpha1)
n2 <- n - n1
x[1:n1] <- rnorm(n1)*sigma1 + miu1
x[(n1+1):n] <- rnorm(n2)*sigma2 + miu2
hist(x,freq=F)
lines(density(x),col='red')

然后计算，修改前的代码计算的结果：

step 30 miu 0.4491562 -2.376833 sigma 2.539587 1.171815 alpha 0.4864524 0.5135476
可以看到偏离真实值非常夸张，根本不可用了。

修改后的结果呢：step 64 miu 2.95897 -1.993656 sigma 1.027112 1.457444 alpha 0.2002033 0.7997967

嗯，参数估计十分接近真实值。

OK，实验结束。所以上面的推断是正确的，如果每个类别的样本数相差不大的话，修改前的计算结果应该是接近修改后的，反之则不然。所以网上的代码还是不能照搬啊，还是得看明白了再用。