40. 组合总和 II

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

所有数字（包括目标数）都是正整数。
解集不能包含重复的组合。
示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2:

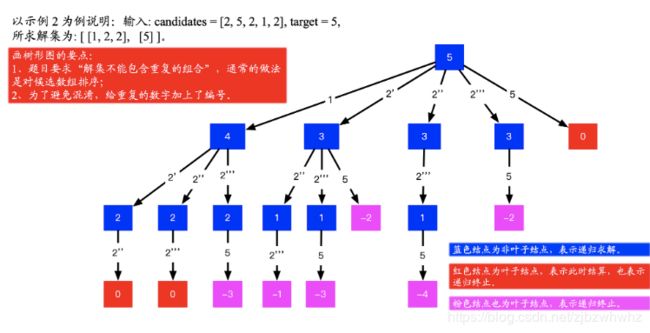
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
  [1,2,2],
  [5]
]

这道题与上一问的区别在于：

• 第 39 题：candidates 中的数字可以无限制重复被选取。
• 第 40 题：candidates 中的每个数字在每个组合中只能使用一次。

编码的不同在于下一层递归的起始索引不一样。

• 第 39 题：还从候选数组的当前索引值开始。
• 第 40 题：从候选数组的当前索引值的下一位开始。

相同之处：解集不能包含重复的组合。

为了使得解集不包含重复的组合。我们想一想，如何去掉一个数组中重复的元素，除了使用哈希表以外，我们还可以先对数组升序排序，重复的元素一定不是排好序以后的第 1 个元素和相同元素的第 1 个元素。根据这个思想，我们先对数组升序排序是有必要的。候选数组有序，对于在递归树中发现重复分支，进而“剪枝”也是有效的。

思路分析

这道题其实比上一问更简单，思路是：

• 以 target 为根结点，依次减去数组中的数字，直到小于 0 或者等于 0，把等于 0 的结果记录到结果集中。
  

这个避免重复当思想是在是太重要了。
这个方法最重要的作用是，可以让同一层级，不出现相同的元素。即
                  1
                 / \
                2   2  这种情况不会发生 但是却允许了不同层级之间的重复即：
               /     \
              5       5
                例2
                  1
                 /
                2      这种情况确是允许的
               /
              2  
                
为何会有这种神奇的效果呢？
首先 cur-1 == cur 是用于判定当前元素是否和之前元素相同的语句。这个语句就能砍掉例1。
可是问题来了，如果把所有当前与之前一个元素相同的都砍掉，那么例二的情况也会消失。 
因为当第二个2出现的时候，他就和前一个2相同了。
                
那么如何保留例2呢？
那么就用cur > begin 来避免这种情况，你发现例1中的两个2是处在同一个层级上的，
例2的两个2是处在不同层级上的。
在一个for循环中，所有被遍历到的数都是属于一个层级的。我们要让一个层级中，
必须出现且只出现一个2，那么就放过第一个出现重复的2，但不放过后面出现的2。
第一个出现的2的特点就是 cur == begin. 第二个出现的2 特点是cur > begin.

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        if len(candidates) == 0:
            return []
        # 剪枝是为了提速，在本题非必需
        candidates.sort()
        # 在遍历的过程中记录路径，它是一个栈
        path = []
        res = []
        # 注意要传入 size ，在 range 中， size 取不到
        self.dfs(candidates, 0, path, res, target)
        return res

    def dfs(self, candidates, begin, path, res, target):
        # 先写递归终止的情况
        if target == 0:
            # Python 中可变对象是引用传递，因此需要将当前 path 里的值拷贝出来
            res.append(path[:])
            return

        for i in range(begin, len(candidates)):
            residue = target - candidates[i]
            # “剪枝”操作，不必递归到下一层，并且后面的分支也不必执行
            if residue < 0:
                break
            if i > begin and candidates[i] == candidates[i-1]:
                continue
            path.append(candidates[i])
            # 因为下一层不能比上一层还小，起始索引还从 index 开始
            
            self.dfs(candidates, i+1, path, res, residue)
            path.pop()

class Solution(object):
    def combinationSum2(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        c = sorted(candidates)
        res = []
        len_c = len(c)
      
        def dfs(target, index, path):

            if target == 0:
                res.append(path)
                return
           
            for i in range(index, len_c):
                
                if i>index and c[i] == c[i-1]:
                    continue
                if c[i]>target:
                    break
                dfs(target-c[i], i+1, path+[c[i]])
        dfs(target, 0, [])
        return res