DBSCAN算法 简单实现 二维/三维结果展示
简介
参考：
https://en.wikipedia.org/wiki/DBSCAN
https://www.cnblogs.com/pinard/p/6208966.html
DBSCAN(Density-based spatial clustering of applications with noise) 最常用的聚类分析算法之一。
该算法以密度为本：给定某空间里的一个点，这算法能把该点附近的点集合成一类（有很多相邻点的点 即高密度区域），并标记出位于低密度区域的局外点（噪音点，最接近它的点也十分远）。
基础知识
DBSCAN 需要两个参数：ε (eps) 和形成高密度区域所需要的最少点数** MinPts**
为了进行 DBSCAN 聚类，所有的点被分为核心点，(密度)可达点及局外点
- ε (eps)
邻域的范围，即在以点p为中心,ε 为半径的圆为p的邻域 - MinPts(领域密度阈值)
判定为核心点(下文解释)邻域内需要的点数(包括自身) - 直接可达
核心点p邻域内的点被称为由 p 直接可达。同时定义，没有任何点是由非核心点直接可达的 - 核心点
如果一个点 p 在距离 ε 范围内有至少 minPts 个点(包括自己)，则这个点被称为核心点 - 密度可达点
如果存在一条道路 p1, …, pn ，有 p1 = p和pn = q， 且每个 pi+1 都是由 pi 直接可达的(道路上除了 q 以外所有点都一定是核心点)，则称 q 是由 p 可达的 - 局外点(噪音)
不由任何点可达的点都被称为局外点
注意：“可达性”（英文：Reachability ）不是一个对称关系，因为根据定义，没有点是由非核心点可达的，但非核心点可以是由其他点可达的。所以为了正式地界定 DBSCAN 找出的聚类，进一步定义两点之间的“连结性”（英文：Connectedness） ：如果存在一个点 o 使得点 p 和点 q 都是由 o 可达的，则点 p 和点 q 被称为(密度)连结的，而连结性是一个对称关系。
总结
如果 p 是核心点，则它与所有由它可达的点(包括核心点和非核心点)形成一个聚类，每个聚类拥有最少一个核心点，非核心点也是聚类的一部分，但它是在聚类的“边缘”位置，因为它不能达至更多的点
算法过程
由一个任意未被访问的点开始，然后探索这个点的 ε-邻域，如果 ε-邻域里有足够的点，则建立一个新的聚类，否则这个点被标签为杂音。注意这个点之后可能被发现在其它点的 ε-邻域里，而该 ε-邻域可能有足够的点，届时这个点会被加入该聚类中。
如果一个点位于一个聚类的密集区域里，它的 ε-邻域里的点也属于该聚类，当这些新的点被加进聚类后，如果它(们)也在密集区域里，它(们)的 ε-邻域里的点也会被加进聚类里。这个过程将一直重复，直至不能再加进更多的点为止，这样，一个密度连结的聚类被完整地找出来。然后，一个未曾被访问的点将被探索，从而发现一个新的聚类或杂音。
代码实现
简单实现 为了方便不再随机挑选点 先将所有核心点挑选出来遍历 未访问到的就是局外点
# -*- coding: utf-8 -*-
"""
Created on Wed Apr 15 16:08:51 2020
@author: alpha
"""
import numpy as np
import matplotlib.pyplot as plt
size = 30
##计算欧式距离
def distEuclid(x,y):
return np.sqrt(np.sum((x-y)**2))
##随机产生n个dim维度的数据 (这里为了展示结果 dim取2或者3)
def genDataset(n,dim):
data = []
while len(data)<n:
p = np.around(np.random.rand(dim)*size,decimals=2)
data.append(p)
return data
##判断两点是否在范围内
def isNeighbor(x,y,eps):
return distEuclid(x,y)<=eps
##获取某一点邻域内的点
def getSeedPos(pos,data,eps):
seed = []
for p in range(len(data)):
if isNeighbor(data[p],data[pos],eps):
seed.append(p)
return seed
##获取核心点列表
def getCorePointsPos(data,eps,minpts):
cpoints=[]
for pos in range(len(data)):
if len(getSeedPos(pos,data,eps))>=minpts:
cpoints.append(pos)
return cpoints
##分类
def getCluster(data,eps,minpts):
corePos = getCorePointsPos(data,eps,minpts)
unvisited =list(range(len(data)))
cluster = {}
num = 0
for pos in corePos:
if pos not in unvisited:
continue
clusterpoint = []
clusterpoint.append(pos)
seedlist = getSeedPos(pos,data,eps)
unvisited.remove(pos)
while seedlist:
p = seedlist.pop(0)
if p not in unvisited:
continue
unvisited.remove(p)
clusterpoint.append(p)
if p in corePos:
seedlist.extend(getSeedPos(p,data,eps))
cluster[num] = clusterpoint
num+=1
cluster["noisy"]=unvisited
return cluster
##展示结果 各类簇使用不同的颜色 中心点使用X表示
def Show(data,cluster):
num,dim = data.shape
color = ['r','g','c','y','m','b','pink','maroon','tomato','peru','lawngreen','gold','aqua','dodgerblue']
##二维图
if dim==2:
for i in cluster:
pos = cluster[i]
if i=="noisy":
for p in pos:
plt.plot(data[p,0],data[p,1],'o',c='k')
else:
for p in pos:
plt.plot(data[p,0],data[p,1],'o',c=color[i])
##三维图
elif dim==3:
ax = plt.subplot(111,projection ='3d')
for i in cluster:
pos = cluster[i]
if i=="noisy":
for p in pos:
ax.scatter(data[p,0],data[p,1],data[p,2],c='black')
else:
for p in pos:
ax.scatter(data[p,0],data[p,1],data[p,2],c=color[i])
plt.show()
data = np.array(genDataset(80,2))
cl = getCluster(data,3,3)
Show(data,cl)
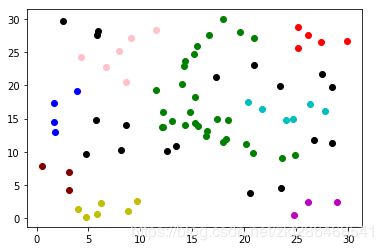
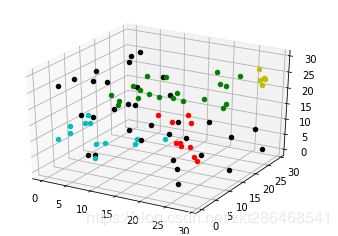
结果展示
注意:
因为数据都是随机生成 并非聚类测试数据 所以结果不是特别好看 仅为模拟算法测试
下图参数：
二维空间80个点
eps=3 minPts=3
每种颜色代表一个集合 黑色代表局外点噪音
下图参数：
三维空间80个点
eps=6 minPts=4
每种颜色代表一个集合 黑色代表局外点噪音
