算法学习----day01如何确定一个点在多面体内

博主一直从事视频图像处理相关工作，由于一些不可抗力因素，必须马上立刻对一些 computer algorithms 有深入的了解，退后，我要开始学习了。

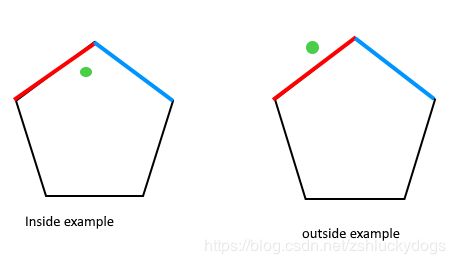
Today‘s  subject：How to check if a given point lies inside a polygon 中文叫如何确定一个给定的点在多面体内。

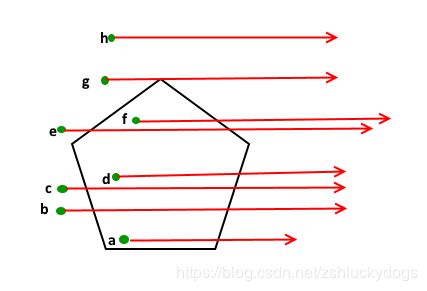
如上图，左边的绿色的点在多面体中，右边的点在多面体外部。具体如何判断呢，简单的说我们可以从绿点 P 发出一条射线，然后统计与多边形的边的交点，如果是奇数则 P （不考虑和多边形顶点共线）则一定是 inside，否则是 outside。见图如下：

先不考虑 g 点的情况，显然如果点 P 在多面体内则与边的交点一定是奇数，否则就是 outside。显而易见的是 g 点也是奇数个交点1，但是 g 在 外部。不用慌，我们接着往下做，判读交点数目奇偶性之后，考虑共线的情况，如果点 P 与多边形当前直线的顶点共线，判断 P 是否位于多边形的当前边，Yes 返回 inside ，No 返回 outside。

这又产生了新的问题：（1）在共线的前提下如何判断一个点是否在线段上（2）如何判断线段相交。

先解决第一个问题，已知三点P，Q，R 共线，如何判断 Q 在线段 PR 上，显然如果 Q 在 PR 上的话，一定满足下面的不等式：

Q.x <= max(P.x, R.x) && Q.x >= min(P.x, R.x) && Q.y <= max(P.y, R.y) && Q.y >= min(P.y, R.y)

接着解决第二个问题，有两种情形，见图如下：

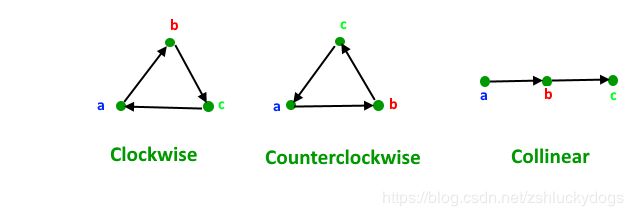
补充概念 Orientations ，对于三元点组（p，q，r）共有三种 orientations，共线、顺时针、逆时针。

假设两条两条线段的顶点分别为 p1，q1，p2，q2，令 
o1 = orientations（p1，q1，p2）
o2 = orientations（p1，q1，q2）
o3 = orientations（p2，q2，p1）
o4 = orientations（p2，q2，p2）

第一种情形： o1 ！= o2 && o3 ！= o4 两条线段一定相交
第二种情形： p1，q1，p2 共线，并且p2在线段 p1q1 上，相交
第三种情形： p1，q1，q2 共线，并且q2在线段 p1q1 上，相交
第四种情形： p2，q2，p1 共线，并且p1在线段 p2q2 上，相交
第五种情形： p2，q2，p2 共线，并且p2在线段 p2q2 上，相交

else 不相交。

Orientation 计算方法：
p，q，r 三点

val = (q.x - p.y) * (r.x -q.x) - (q.x - p.x) * (r.y - q.y)
val == 0 共线
val > 0 顺时针方向
val < 0 逆时针方向

之后就是实现过程了，给出简单的描述：

step1：输入多边形的顶点，顶点数必须大于等于4，输入点 P，交点数目 count := 0;

step2:  从点 P 引一条射线 P->extreme，当前多边形的边 polygon[i]->polygon[next]

           next := (i+1)%n;

           if  P->extreme 与 polygon[i]->polygon[next] 相交；

                   if P、polygon[i]、polygon[next] 的oreintatons := 0，即共线；

                            if  P 在边 polygon[i]->polygon[next] 上；

                                    return  inside

                            end if

                   count ++；

           i = next；

step3：while i != 0，do step2；

step4：if  count%2 ==1，return inside.

 

Bingo！

给出 C++实现的代码：

#include
using namespace std;
#define INF 10000
struct Point
{
    int x;
    int y;

};
bool onSegment(Point p, Point q, Point r)
{
    if (q.x <= max(p.x, r.x) && q.x >= min(p.x, r.x) && q.y <= max(p.y, r.y) && q.y >= min(p.y, r.y))
        return true;

    return false ;    
}
int orientation(Point p, Point q, Point r)
{
    int val = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
    if (val == 0) return 0;
    return (val >0)? 1: 2;
}
bool doIntersect(Point p1, Point q1, Point p2, Point q2) 
{ 
    // Find the four orientations needed for general and 
    // special cases 
    int o1 = orientation(p1, q1, p2); 
    int o2 = orientation(p1, q1, q2); 
    int o3 = orientation(p2, q2, p1); 
    int o4 = orientation(p2, q2, q1); 
  
    // General case 
    if (o1 != o2 && o3 != o4) 
        return true; 
  
    // Special Cases 
    // p1, q1 and p2 are colinear and p2 lies on segment p1q1 
    if (o1 == 0 && onSegment(p1, p2, q1)) return true; 
  
    // p1, q1 and q2 are colinear and q2 lies on segment p1q1 
    if (o2 == 0 && onSegment(p1, q2, q1)) return true; 
  
    // p2, q2 and p1 are colinear and p1 lies on segment p2q2 
    if (o3 == 0 && onSegment(p2, p1, q2)) return true; 
  
     // p2, q2 and q1 are colinear and q1 lies on segment p2q2 
    if (o4 == 0 && onSegment(p2, q1, q2)) return true; 
  
    return false; // Doesn't fall in any of the above cases 
} 

bool isInside(Point polygon[], int n, Point p) 
{ 
    // There must be at least 3 vertices in polygon[] 
    if (n < 3)  return false; 
  
    // Create a point for line segment from p to infinite 
    Point extreme = {INF, p.y}; 
  
    // Count intersections of the above line with sides of polygon 
    int count = 0, i = 0; 
    do
    { 
        int next = (i+1)%n; 
  
        // Check if the line segment from 'p' to 'extreme' intersects 
        // with the line segment from 'polygon[i]' to 'polygon[next]' 
        if (doIntersect(polygon[i], polygon[next], p, extreme)) 
        { 
            // If the point 'p' is colinear with line segment 'i-next', 
            // then check if it lies on segment. If it lies, return true, 
            // otherwise false 
            if (orientation(polygon[i], p, polygon[next]) == 0) 
               return onSegment(polygon[i], p, polygon[next]); 
  
            count++; 
        } 
        i = next; 
    } while (i != 0); 
  
    // Return true if count is odd, false otherwise 
    return count&1;  // Same as (count%2 == 1) 
} 
int main() 
{ 
    Point polygon1[] = {{0, 0}, {10, 0}, {10, 10},{5,15}, {0, 10}}; 
    int n = sizeof(polygon1)/sizeof(polygon1[0]); 
    Point p = {5, 5}; 
    isInside(polygon1, n, p)? cout << "Yes \n": cout << "No \n"; 
    
   /* Point  p = {5, 5}; 
    isInside(polygon1, n, p)? cout << "Yes \n": cout << "No \n"; 
  
    Point polygon2[] = {{0, 0}, {5, 5}, {5, 0}}; 
    Point p = {3, 3}; 
    n = sizeof(polygon2)/sizeof(polygon2[0]); 
    isInside(polygon2, n, p)? cout << "Yes \n": cout << "No \n"; 
  
    Point p = {5, 1}; 
    isInside(polygon2, n, p)? cout << "Yes \n": cout << "No \n"; 
  
    Point p = {8, 1}; 
    isInside(polygon2, n, p)? cout << "Yes \n": cout << "No \n"; 
  
    Point polygon3[] =  {{0, 0}, {10, 0}, {10, 10}, {0, 10}}; 
    Point p = {-1,10}; 
    n = sizeof(polygon3)/sizeof(polygon3[0]); 
    isInside(polygon3, n, p)? cout << "Yes \n": cout << "No \n"; */
    

    return 0; 
}