【Matlab】使用yalmip和cplex求解器求解规划问题
1.yalmip简介
yalmip是由Lofberg开发的一种免费的优化求解工具,其最大特色在于集成许多外部的最优化求解器(包括cplex),形成一种统一的建模求解语言,提供了Matlab的调用API,减少学习者学习成本。简而言之,它可以让你像书写数学模型那样输入你的模型。
2.环境搭建
2.1 yalmip安装
yalmip下载页面,点击下载即可。
解压后,将其复制到toolbox文件夹下面。
打开matlab,在home选项卡里面找setpath(设置路径)。
注意:有些matlab的doc可能不能使用,因此doc yalmip可能会报错,不必担心。
2.2 cplex安装
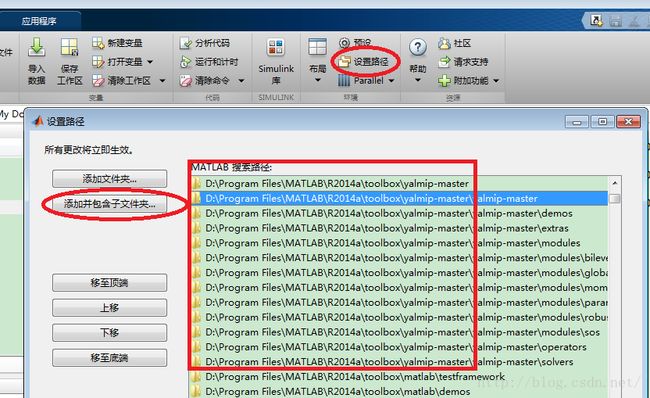
若您已经安装了cplex studio,可以在matlab菜单栏中找到设置路径(set path)的选项,选择“添加并包含子文件夹”,将cplex安装路径的cplex\matlab这一个文件夹添加进去。如下图所示。
若您没有安装cplex studio,也没有关系。可以直接下载简化版,如下图所示。
下载地址已经放在了csdn上,本博客最下方也提供了百度云链接。
下载解压之后,接着,同样需要像上面一样配置路径。
matlab版本2015a上亲测可用,效果如下图。
3. 使用方法
yalmip求解优化问题四部曲
3.1 创建决策变量
yalmip一共有三种方式创建决策变量,分别为:
- sdpvar-创建实数型决策变量
- intbar-创建整数型决策变量
- binvar-创建0/1型决策变量
不过值得注意的是,在创建n*n的决策变量时,yalmip默认是对称方阵,所以要创建非对称方针时,需要这样写:
xxxvar(n,n,'full')
3.2 添加约束条件
比起matlab自带的各种优化函数所要写明的约束条件,yalmip的约束条件写起来是非常舒适直观的。
例如:0<=x1+x2+x3<=1,可以这样写(非常直观简介):
% 创建决策变量
x = sdpvar(1,3);
% 添加约束条件
C = [0<=x(1)+x(2)+x(3)<=1];3.3 参数配置
关于参数设置,我们大多数是用来设置求解器solver的,如下所示。
%设置求解器为cplex
options=sdpsettings('solver','cplex');3.4 求解问题
首先要明确求解目标z,yalmip默认是求解最小值问题,所以遇到求解最大值的问题,只需要在原问题的基础上添加一个负号即可。求解调用格式如下所示。
%求解
optimize(target,constraints,opstions)3.5 举例
3.5.1 求解如下非线性规划问题
% 清除工作区
clear;clc;close all;
% 创建决策变量
x = sdpvar(1,2);
% 添加约束条件
C = [
x(1) + x(2) >= 2
x(2)-x(1) <=1
x(1)<=1
];
% 配置
ops = sdpsettings('verbose',0,'solver','cplex');
% 目标函数
z = -(x(1)+2*x(2))/(2*x(1)+x(2)); % 注意这是求解最大值
% 求解
reuslt = optimize(C,z);
if reuslt.problem == 0 % problem =0 代表求解成功
value(x)
-value(z) % 反转
else
disp('求解出错');
end执行结果如下
First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 1 0.000000e+00 2.000e+00 1.845e+00
1 2 -1.361410e+00 5.242e-01 7.089e-01 1.602e+00
2 3 -1.308814e+00 4.441e-16 7.788e-01 8.140e-01
3 4 -1.299288e+00 0.000e+00 9.851e-02 8.490e-02
4 5 -1.333584e+00 4.441e-16 1.095e-01 7.327e-02
5 6 -1.364417e+00 4.441e-16 2.942e-02 7.491e-02
6 7 -1.360272e+00 0.000e+00 2.021e-02 8.267e-03
7 8 -1.379966e+00 4.441e-16 2.129e-02 5.706e-02
8 9 -1.387834e+00 4.441e-16 3.065e-02 5.399e-02
9 11 -1.391538e+00 4.441e-16 3.738e-02 2.721e-02
10 12 -1.392332e+00 0.000e+00 4.000e-03 6.714e-03
11 13 -1.398128e+00 4.441e-16 7.445e-03 2.336e-02
12 14 -1.398413e+00 0.000e+00 3.518e-03 6.077e-04
13 15 -1.398400e+00 0.000e+00 8.000e-04 2.893e-05
14 16 -1.399667e+00 0.000e+00 1.513e-03 5.037e-03
15 17 -1.399680e+00 0.000e+00 2.062e-04 1.052e-04
16 18 -1.399680e+00 4.441e-16 1.600e-04 1.719e-06
17 19 -1.399935e+00 0.000e+00 3.110e-04 1.024e-03
18 20 -1.399936e+00 0.000e+00 3.200e-05 9.170e-07
19 21 -1.399999e+00 0.000e+00 7.509e-05 2.535e-04
20 22 -1.399999e+00 4.441e-16 3.200e-07 3.477e-08
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the selected value of the function tolerance,
and constraints are satisfied to within the selected value of the constraint tolerance.
ans =
0.5000 1.5000
ans =
1.4000 3.5.2 求解经典TSP问题
% 利用yamlip求解TSP问题
clear;clc;close all;
d = load('E:\\tsp_dist_matrix.txt')';
n = size(d,1);
% 决策变量
x = binvar(n,n,'full');
u = sdpvar(1,n);
% 目标
z = sum(sum(d.*x));
% 约束添加
C = [];
for j = 1:n
s = sum(x(:,j))-x(j,j);
C = [C, s == 1];
end
for i = 1:n
s = sum(x(i,:)) - x(i,i);
C = [C, s == 1];
end
for i = 2:n
for j = 2:n
if i~=j
C = [C,u(i)-u(j) + n*x(i,j)<=n-1];
end
end
end
% 参数设置
ops = sdpsettings('verbose',0,'solver','cplex');
% 求解
result = optimize(C,z);
if result.problem== 0
value(x)
value(z)
else
disp('求解过程中出错');
end其中,用到了tsp_dist_matrix.txt文件,内容如下。
0 7 4 5 8 6 12 13 11 18
7 0 3 10 9 14 5 14 17 17
4 3 0 5 9 10 21 8 27 12
5 10 5 0 14 9 10 9 23 16
8 9 9 14 0 7 8 7 20 19
6 14 10 9 7 0 13 5 25 13
12 5 21 10 8 13 0 23 21 18
13 14 8 9 7 5 23 0 18 12
11 17 27 23 20 25 21 18 0 16
18 17 12 16 19 13 18 12 16 0运行结果如下
Tried aggregator 1 time.
Reduced MIP has 92 rows, 99 columns, and 396 nonzeros.
Reduced MIP has 90 binaries, 0 generals, 0 SOSs, and 0 indicators.
Presolve time = 0.03 sec. (0.19 ticks)
Probing time = 0.02 sec. (0.16 ticks)
Tried aggregator 1 time.
Reduced MIP has 92 rows, 99 columns, and 396 nonzeros.
Reduced MIP has 90 binaries, 0 generals, 0 SOSs, and 0 indicators.
Presolve time = -0.00 sec. (0.19 ticks)
Probing time = -0.00 sec. (0.17 ticks)
Clique table members: 56.
MIP emphasis: balance optimality and feasibility.
MIP search method: dynamic search.
Parallel mode: deterministic, using up to 4 threads.
Root relaxation solution time = 0.08 sec. (0.15 ticks)
Nodes Cuts/
Node Left Objective IInf Best Integer Best Bound ItCnt Gap
0 0 74.6000 20 74.6000 27
0 0 77.0000 20 Cuts: 7 33
* 0+ 0 77.0000 77.0000 33 0.00%
0 0 cutoff 77.0000 77.0000 33 0.00%
Elapsed time = 0.33 sec. (3.33 ticks, tree = 0.00 MB, solutions = 1)
Clique cuts applied: 4
Mixed integer rounding cuts applied: 1
Multi commodity flow cuts applied: 2
Root node processing (before b&c):
Real time = 0.33 sec. (3.34 ticks)
Parallel b&c, 4 threads:
Real time = 0.00 sec. (0.00 ticks)
Sync time (average) = 0.00 sec.
Wait time (average) = 0.00 sec.
------------
Total (root+branch&cut) = 0.33 sec. (3.34 ticks)
ans =
NaN 0 0 1 0 0 0 0 0 0
0 NaN 0 0 0 0 1 0 0 0
0 1 NaN 0 0 0 0 0 0 0
0 0 1 NaN 0 0 0 0 0 0
0 0 0 0 NaN 1 0 0 0 0
0 0 0 0 0 NaN 0 1 0 0
0 0 0 0 1 0 NaN 0 0 0
0 0 0 0 0 0 0 NaN 0 1
1 0 0 0 0 0 0 0 NaN 0
0 0 0 0 0 0 0 0 1 NaN
ans =
77本文引用的其他博主的博客内容均有指明,对此表示感谢。有读者问如何解码最后的邻接矩阵,先给出笔者的做法:
a=[NaN 0 0 1 0 0 0 0 0 0
0 NaN 0 0 0 0 1 0 0 0
0 1 NaN 0 0 0 0 0 0 0
0 0 1 NaN 0 0 0 0 0 0
0 0 0 0 NaN 1 0 0 0 0
0 0 0 0 0 NaN 0 1 0 0
0 0 0 0 1 0 NaN 0 0 0
0 0 0 0 0 0 0 NaN 0 1
1 0 0 0 0 0 0 0 NaN 0
0 0 0 0 0 0 0 0 1 NaN];
%初始时,从第一行开始
k = 1;
path = [k];
for i=1:size(a,1)
%寻找当前行k中的1所在的位置
for j=1:size(a,2)
if(a(k,j) == 1)
k = j;
path = [path, k];
break;
end
end
end
pathpath =
1 4 3 2 7 5 6 8 10 9 1由于看到大家需求比较大,这里直接放在百度网盘上了,需要的话去下载就行了。
链接:https://pan.baidu.com/s/1Zj0JEFNKC7kwmaaBWeOKtQ
提取码:k497