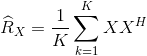MUSIC算法推导及代码实现

---

简介

MUSIC (Multiple Signal Classification)算法，即多信号分类算法，由Schmidt等人于1979年提出。MUSIC算法是一种基于子空间分解的算法，它利用信号子空间和噪声子空间的正交性，构建空间谱函数，通过谱峰搜索，估计信号的参数。对于声源定位来说，需要估计信号的DOA。MUSIC算法对DOA的估计有很高的分辨率，且对麦克风阵列的形状没有特殊要求，因此应用十分广泛。

---

原理

MUSIC算法是基于远场窄带信号的子空间算法，经典的远场窄带DOA估计的阵列信号模型如图1，

图 1 经典DOA估计阵列信号模型

1. 数学模型

远场窄带DOA估计数学模型为，

其中，为采样点数，为M个阵元的输出，为方向响应向量，P为信号源的数量，为入射信号，为阵列噪声。

2. 计算协方差矩阵

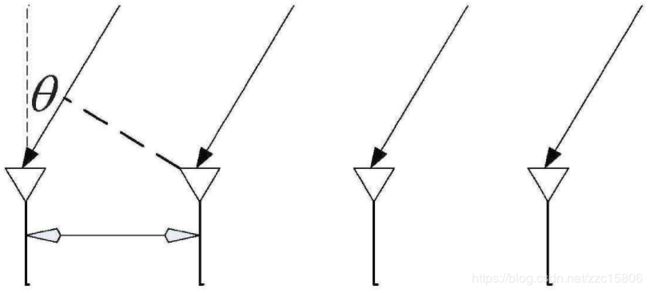
由于各阵元的噪声互不相关，也不和信号相关，因此X(n)的协方差矩阵为，

其中，表示入射信号的协方差矩阵，操作为复共轭转置。

实际上，采集的接收数据矩阵是有限长的，需要对有限的采样数据的协方差矩阵进行最大似然估计，

3. 进行特征值分解

对该协方差矩阵进行特征值分解，对分解得到的特征值进行大小排列，把与信号源数量P相等的最大的P个特征值所对应的特征向量组成的特征空间，称为信号子空间，即；把剩下的(M-P)个特征值对应的特征向量组成的特征空间称为噪声子空间，即,

4. 构建空间谱，

空间谱计算公式如下，

进行谱峰搜索，的个极大值对应的就是信号源的方向。

---

实验仿真

对于一维均匀线性阵列（ULA，Uniform Linear Array），每个阵元等间距线性排列，其MUSIC算法如下：

clear; close all;
%%%%%%%% MUSIC for Uniform Linear Array%%%%%%%%
derad = pi/180;
N = 8;               % 阵元个数        
M = 3;               % 信源数目
theta = [-30 0 60];  % 待估计角度
snr = 10;            % 信噪比
K = 512;             % 快拍数

dd = 0.5;            % 阵元间距 
d=0:dd:(N-1)*dd;
A=exp(-1i*2*pi*d.'*sin(theta*derad));
% 构建信号模型
S=randn(M,K); X=A*S;
X1=awgn(X,snr,'measured');
% 计算协方差矩阵
Rxx=X1*X1'/K;
% 特征值分解
[EV,D]=eig(Rxx);
EVA=diag(D)';
[EVA,I]=sort(EVA);
EV=fliplr(EV(:,I));
En=EV(:,M+1:N);    % 信号子空间

% 遍历每个角度，计算空间谱
for iang = 1:361
    angle(iang)=(iang-181)/2;
    phim=derad*angle(iang);
    a=exp(-1i*2*pi*d*sin(phim)).';    
    Pmusic(iang)=1/(a'*En*En'*a);
end
Pmusic=abs(Pmusic);
Pmusic=10*log10(Pmusic);
h=plot(angle,Pmusic);
set(h,'Linewidth',0.5);
xlabel('入射角/(degree)');
ylabel('空间谱/(dB)');
set(gca, 'XTick',[-90:30:90]);
grid on;

对于二维均匀圆阵（UCA，Uniform Circle Array），每个阵元等间角度的分布在半径为r的圆周上。其MUSIC算法如下：

clear all; close all;
%%%%%%%% MUSIC for Uniform Circle Array%%%%%%%%
r=1;                                            % 半径(m)
N=16;                                           % 阵元数目
d=2*r*sin(pi/N);

M=1;                                            % 信源数量
gamma=2*pi/N*(0:N-1);                           % 和参考阵元的角度
fc=16000;                                       % 采样率
c=340;                                          % 声音的速度（m/s）
lambda=c/fc;

a_theta=45;                                     % 仰角
a_phi=90;                                       % 方位角

zeta=2*pi/lambda*r*sin(a_theta*pi/180);
A=exp(1i*zeta*cos((a_phi-gamma)*pi/180)).';     % 导向矢量

K=100;                                          % 快拍数
t=(0:K-1)/1000;

% 构建信号模型
S=sin(2*pi*fc*t);
X=A*S;
snr=10;
X1=awgn(X,snr,'measured');
% 计算协方差矩阵
R=X1*X1'/K;
% 特征值分解
[Q,D]=eig(R);
[D,I]=sort(diag(D),1,'descend');
Q=Q(:,I);
Qn=Q(:,M+1:N);                                  % 信号子空间

theta=0:90;
phi=0:1:360;

p_MUSIC=zeros(length(theta),length(phi));

for ii=1:length(theta)
    for iii=1:length(phi)
        zeta=2*pi/lambda*r*sin(theta(ii)*pi/180);
        A=exp(1i*zeta*cos((phi(iii)-gamma)*pi/180)).';
        p_MUSIC(ii,iii)=(1/(A'*(Qn*Qn')*A));
    end
end

mesh(phi,theta,abs(p_MUSIC))
grid on;xlabel('仰角');ylabel('方位角');zlabel('PMUSIC');title('UCA MUSIC');