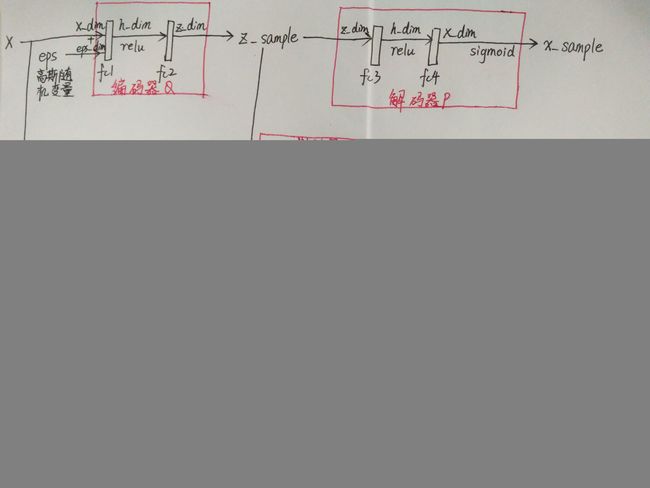
对抗变分贝叶斯：变分自编码器与生成对抗网络的统一 （一）
最近在学习VAE(变分自编码器)， 在github上找到了有关VAE、GAN的许多代码，github链接如下：
https://github.com/wiseodd/generative-models
我试了试在VAE/adversarial_vb/文件夹中的 AVB代码，并找到了对应的论文Adversarial Variational Bayes: Unifying Variational Autoencoders and Generative Adversarial Networks，链接如下：
https://arxiv.org/abs/1701.04722
关于论文的研读我之后再写出来，这里为方便入手，先把github代码贴出来：
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import torch
import torch.nn
import torch.nn.functional as nn
import torch.autograd as autograd
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import os
from torch.autograd import Variable
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('../../MNIST_data', one_hot=True)
mb_size = 32 # batch_size
z_dim = 10
eps_dim = 4
X_dim = mnist.train.images.shape[1]
y_dim = mnist.train.labels.shape[1]
h_dim = 128
cnt = 0
lr = 1e-3 # 学习率
def log(x):
return torch.log(x + 1e-8)
# Encoder: q(z|x,eps) # 编码器
Q = torch.nn.Sequential(
torch.nn.Linear(X_dim + eps_dim, h_dim), # 一个全连接层
torch.nn.ReLU(),
torch.nn.Linear(h_dim, z_dim) # 一个全连接层
)
# Decoder: p(x|z) # 解码器
P = torch.nn.Sequential(
torch.nn.Linear(z_dim, h_dim), # 一个全连接层
torch.nn.ReLU(),
torch.nn.Linear(h_dim, X_dim), # 一个全连接层
torch.nn.Sigmoid()
)
# Discriminator: T(X, z) # 判别器
T = torch.nn.Sequential(
torch.nn.Linear(X_dim + z_dim, h_dim), # 一个全连接层
torch.nn.ReLU(),
torch.nn.Linear(h_dim, 1) # 一个全连接层 # 输出为一维，即一个数
)
def reset_grad(): # 重置梯度为0
Q.zero_grad()
P.zero_grad()
T.zero_grad()
def sample_X(size, include_y=False): # 对输入进行采样
X, y = mnist.train.next_batch(size)
X = Variable(torch.from_numpy(X))
if include_y:
y = np.argmax(y, axis=1).astype(np.int)
y = Variable(torch.from_numpy(y))
return X, y
return X
Q_solver = optim.Adam(Q.parameters(), lr=lr) # 三个模块的优化求解器
P_solver = optim.Adam(P.parameters(), lr=lr)
T_solver = optim.Adam(T.parameters(), lr=lr)
for it in range(1000000): # 开始迭代
X = sample_X(mb_size) # 输入为从训练集中采样并进行类型转换后的数据
eps = Variable(torch.randn(mb_size, eps_dim))
z = Variable(torch.randn(mb_size, z_dim)) # 由标准正态分布（均值为0,方差为1）中随机采样
# Optimize VAE # 优化变分自编码器
z_sample = Q(torch.cat([X, eps], 1))
X_sample = P(z_sample)
T_sample = T(torch.cat([X, z_sample], 1))
disc = torch.mean(-T_sample) # 判别器输出的负数的均值
loglike = -nn.binary_cross_entropy(X_sample, X, size_average=False) / mb_size
# 交叉熵， 最小化交叉熵损失函数等价于最大化对数似然， 让重构图像尽可能接近原始输入图像
elbo = -(disc + loglike) # 证据下界， 常用在变分推断中
elbo.backward() # 证据下界反向传播，优化编码器与解码器
Q_solver.step()
P_solver.step()
reset_grad() # 重置梯度为0
# Discriminator T(X, z) # 对于判别器，优化判别器
z_sample = Q(torch.cat([X, eps], 1))
T_q = nn.sigmoid(T(torch.cat([X, z_sample], 1)))
T_prior = nn.sigmoid(T(torch.cat([X, z], 1)))
T_loss = -torch.mean(log(T_q) + log(1. - T_prior))
T_loss.backward()
T_solver.step()
reset_grad() # 重置梯度为0
# Print and plot every now and then
if it % 1000 == 0:
print('Iter-{}; ELBO: {:.4}; T_loss: {:.4}'
.format(it, -elbo.data[0], -T_loss.data[0]))
samples = P(z).data.numpy()[:16] # 高斯随机变量输入解码器后的输出
fig = plt.figure(figsize=(4, 4)) # python 画图
gs = gridspec.GridSpec(4, 4)
gs.update(wspace=0.05, hspace=0.05)
for i, sample in enumerate(samples): # 遍历每个结果
ax = plt.subplot(gs[i])
plt.axis('off')
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.set_aspect('equal')
plt.imshow(sample.reshape(28, 28), cmap='Greys_r')
if not os.path.exists('out/'):
os.makedirs('out/')
plt.savefig('out/{}.png'
.format(str(cnt).zfill(3)), bbox_inches='tight') # 保存随机变量解码后的图像
cnt += 1
plt.close(fig)
代码中我写了自己的注释，并自己画了一张计算流程图如下所示：
这次写作比较草率，如果有不恰当或错误的地方还请及时指出～