FP-Growth 和 K-Means 学习报告

最近学习了数据挖掘常用的两种算法：FP-Growth 和 K-Means。现在把我的学习结果分享给大家。

以下是本文的目录，大家可以根据需要跳过一些章节：

• 1. FP-Growth
  
  • 1.1 支持度计数筛选
  • 1.2 步骤简介
  • 1.3 实例分析
    
    • 1.3.1 Overview
    • 1.3.2 如何把不同行的数据聚到一行？
    • 1.3.3 如何把 FP-Growth 算法的输出还原成类似于输入的事务？
    • 1.3.4 处理结果与应用场合
• 2. K-Means
  
  • 2.1 分类原理
    
    • 2.1.1 欧几里得距离的高效计算
    • 2.1.2 计算质心的方法：
  • 2.2 步骤简介
  • 2.3 计算实例
  • 2.4 实现要点
• 3.Reference

文中的引用以上标表示。所有源代码都可以在我的 GitHub：https://github.com/K9A2/DataMining 上找到。大家也可以到我的网站查看更多新鲜内容：http://www.stormlin.com。

1. FP-Growth

---

在生活中，我们常常会遇到一些需要分析事物之间的关联性的场合。例如，在分析超市的销售数据时，我们可能会想知道，顾客在买牛奶的时候，还会买什么别的东西。还有数据挖掘领域里面著名的啤酒与尿布的故事^R1。

要解决这些问题，我们就需要一种算法来帮我们寻找这些事务项之间的关联性。常用的关联分析（Association Analysis）
算法有 Apriori 算法和 FP-Growth 算法。Apriori 算法的时空复杂度都比较高，现在已经不常用了，故本文略去对 Apriori 算法的介绍，专注于对 FP-Growth 的介绍与分析。

1.1 支持度计数筛选

在 FP-Growth 算法里面，需要对每一个事项计算各自的支持度计数（即此事务在全集中出现的次数）。如果支持度不满足设定的最小值，那么这项记录将不能被算法所收录。

1.2 步骤简介

FP-Growth 的步骤相对于 Apriori 会简单一点，但绝对值也不低。其伪代码步骤简介如下^R5：

输入：事务集合 List> transactions
输出：频繁模式集合 List> fpOutput

public void getFPOutput(List> transactions, List postPattern, List> fpOutput) {
    构建头表项 HeaderTable：buildHeaderTable(transactions);
    构建 FP 树：buildFPTree(headerTable, transactions);
    if (树空) return;
    输出频繁项集;
    遍历每一个头项表节点并递归;
}

具体操作步骤请参考源代码。

1.3 实例分析

1.3.1 Overview

针对 FP-Growth 的实例分析，我们采用了一个具有 27 万测试数据的数据集（示例见 Fig.1，可以通过度盘链接下载）。在经过预处理阶段之后（即源代码中的 preProcess 方法），数据量下降为 6 万多。包括预处理、FP-Growth 计算频繁项集和重整输出三个阶段的完整流程的处理时间为 10 秒。

Fig.1 Data Sample

1.3.2 如何把不同行的数据聚到一行？

通过观察，我们可以发现，每一条记录都是独立一行的。那么我们就需要把这些记录合并到同一行中，形成一个类似于购物篮分析中所用的数据集。

在这个数据集中，每一个行都是由读者记录号、图书记录号（种）以及图书分类号等组成的。同时，由于这是一个日志文件，那么就可以通过相同的上下文来确定一项事务中所包含的各项。

1.3.3 如何把 FP-Growth 算法的输出还原成类似于输入的事务？

FP-Growth 算法输出是杂乱无章的，所以我们就需要对它的输出进行重整。而为了尽可能扩大相关联事务的范围，我们采用了合并所有有交集的行的方法：

private static void getResultFiltered(List> result, List> removedPrefix) {
    //合并与去重
    HashSet temp = new HashSet<>();
    int elementLeft = removedPrefix.size();
    //任意两行之间如果有交集，就合并他们
    while (removedPrefix.size() != 0) {
        temp.addAll(removedPrefix.get(0));
        for (int j = 1; j < elementLeft - 1; j++) {
            //若两项之间有交集，则 isIntersected 返回 true
            if (isIntersected(temp, removedPrefix.get(j))) {
                temp.addAll(removedPrefix.get(j));
                removedPrefix.remove(j);
                elementLeft--;
                j--;
            }
        }
        result.add(new ArrayList<>(temp));
        temp.clear();
        elementLeft--;
        removedPrefix.remove(0);
    }
}

以上算法中，HashSet 的使用有效加快了匹配的速度。同时，由于算法会删去已添加的行，重整算法的时间复杂度近似为 O(nlogn)，空间复杂度不会超过输入数组的大小，即 O(n)。

1.3.4 处理结果与应用场合

本算法能在给定的事务集中高效计算频繁项集。那么，我们就能把这个算法移植到服务器端，并在小数据量的情况下实现根据用户的指定的类别，实时计算频繁项集，并在结果页面推荐给用户。

2. K-Means

---

在对数据进行了关联分析之后，有时候还需要对数据进行聚簇分析（Clustering Analysis）。聚类分析的算法较多，这里只介绍 K-Means 算法。这个算法的输入有数据集和分类数目 K；输出是分在 K 个簇中的数据项。

2.1 分类原理

分类主要涉及计算欧几里得距离和计算一群质点的质心两个算法，下面分别介绍：

2.1.1 欧几里得距离的高效计算

分类的方法主要是计算某个点与所有 K 个质心之间的欧几里得距离。计算两个 n 维点之间的欧几里得距离^R4：

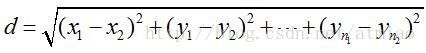
Fig.2 EuclidDistance

实用的计算方法：

private static double getEuclidDistance(Point a, Point b) {
    double result = 0;
    result += Math.pow(a.getX() - b.getX(), 2);
    result += Math.pow(a.getY() - b.getY(), 2);
    result += Math.pow(a.getZ() - b.getZ(), 2);
    return Math.sqrt(result);
}

2.1.2 计算质心的方法：

在 K-Means 算法中，分类需要按照欧几里得距离最小的原则。但在实用的算法中，通常采用重心来代替质心：

private static Point getClusterCenter(List points) {
    if (points.size() == 0) {
        return null;
    }
    if (points.size() == 1) {
        return new Point(points.get(0).getX(), points.get(0).getY(), points.get(0).getZ());
    }
    double x = 0;
    double y = 0;
    double z = 0;
    for (Point point : points) {
        x += point.getX();
        y += point.getY();
        z += point.getZ();
    }
    x = x / points.size();
    y = y / points.size();
    z = z / points.size();
    return new Point(x, y, z);
}

2.2 步骤简介

K-Means 算法是一种很好理解的算法，其步骤异常简单。

1. 用户提供输入数据集。数据集中的每一项都需要包含若干属性。如输入一个二维点集，那其中的一项就需要至少包含 X 和 Y 两个坐标；
2. 由用户指定初始质心或者由算法在输入的数据集中随机选取 K 个点作为初始质心；
3. 计算每一项到每一个质心之间的欧几里得距离；
4. 按照欧几里得距离最小的原则，把这些点分到 K 个簇中的某一个；
5. 重新计算 K 个簇中的质心（通常用计算重心代替）；
6. 如果质心与分类时使用的质心相同，则算法结束；否则就需要重复 2-6 步。

2.3 计算实例

由于每一个点不仅仅需要保存自身的三轴坐标，同时还要保存自身的类别以及名字，故新建了用于表示点的 Point 类，并以 Point[] 来表示点集。

计算实例采用了 CPDA 数据分析天地提供的足球数据^R3。由于设计的时候采用了三维点集，所以无法采用通常的二维分类着色图^R2来表示，故直接输出三种分类。其实验结果如下：

日本,韩国,澳大利亚,
印尼,泰国,
中国,朝鲜,伊拉克,伊朗,沙特,阿联酋,卡塔尔,乌兹别克斯坦,巴林,阿曼,约旦,

其结果符合球队实际排位。

另外，由于本次实验中尚未添加对分类的排序功能，即在输出的时候并非按照质心的“权重”来进行排序，故输出的结果是不能直接提取到别的程序中的。

2.4 实现要点

• 随机初始质心的获取

  获取随机初始质心有两种方法：

  • 第一种是采用 Collection.shuffle() 来直接打乱排序，然后直接取前 K 位作为随机初始质心；
  • 第二种就是使用随机数。先计算出 K 个不重复的随机数，然后按照获得的随机数到 Point[] 数组中获取随机初始质心，其计算过程如下：
    

    private static int[] getUnrepeatedRandomNumbers(int min, int max, int count) {
        int[] result = new int[count];
        int i = 0;
        HashSet temp = new HashSet<>();
        while (true) {
            if (temp.size() == count) {
                break;
            }
            temp.add((int) (Math.random() * (max - min)) + min);
        }
        for (Integer item : temp) {
            result[i] = item;
            i++;
        }
        return result;
    }

• Point[] 数组的复制与判同

  • 如果直接调用系统提供的 System.arraycopy(b, 0, a, 0, a.length)，那在复制的时候就是浅复制：即两个数组都是“引用了”同一个来源。在其中一个数组被改变的时候，另外一个数组由于引用了同一块内存区域，其值也会被改变。故要实现数组的“深拷贝”，则需要自行编写复制方法：

    private static Point[] getArrayCopy(Point[] b) {
    
        Point[] a = new Point[b.length];
    
        if (a.length == 0 || b.length == 0) {
            return null;
        }
    
        System.arraycopy(b, 0, a, 0, a.length);
    
        return a;
    }

  • 那么如何判断两个质心是否移动呢？我们可以直接采用逐行判断的方式：

    private static boolean isClusterCenterChanged(Point[] a, Point[] b) {
        for (int i = 0; i < a.length; i++) {
            if (a[i].getX() != b[i].getX()) {
                return true;
            } else if (a[i].getY() != b[i].getY()) {
                return true;
            } else if (a[i].getZ() != b[i].getZ()) {
                return true;
            }
        }
        return false;
    }

  在任意一次比较中，如果两者的 X、Y 和 Z 三个值中的任意一个不相等，方法就会返回 true，即质心已移动；否则返回 false，表示质心未移动。

3.Reference

1. Grant Stanley - Diapers, Beer, and Data Science in Retail
2. 听云博客 - JAVA实现K-means聚类
3. CPDA 数据分析天地 - 用K-means看透中国男足！
4. tianlan_new_start - 欧几里得距离、曼哈顿距离和切比雪夫距离
5. 人非木石_xst - 单机和集群环境下的FP-Growth算法java实现(关联规则挖掘)