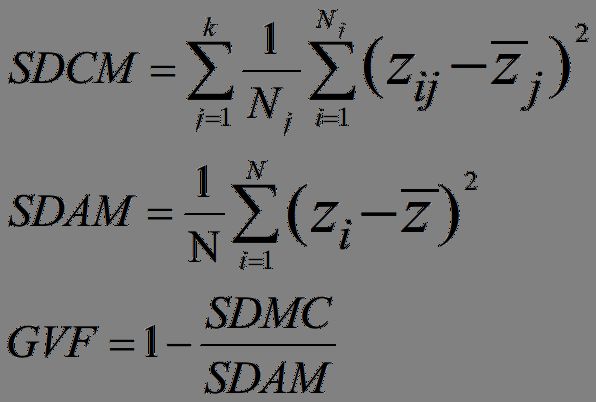数据分类那些事儿

原文链接：http://hmfly.info/2012/10/17/mercator那些事儿/

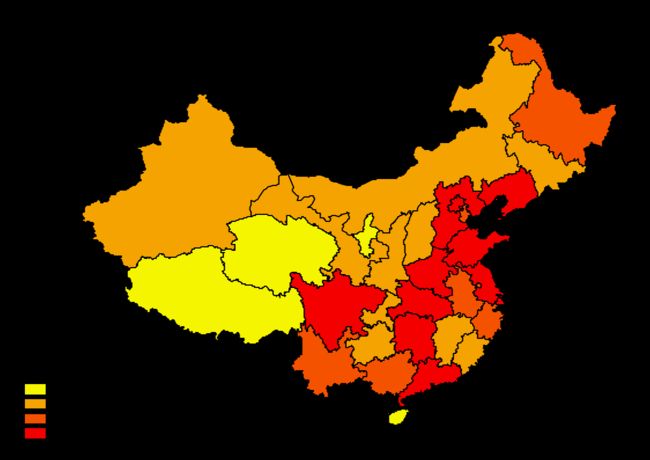
数据分类、地图分级（Classification）通常用于Choropleth Map（面量图）的制作中，是专题制图中最初，也是最基本的一个步骤。没有进行过分类的地图，很难让人理解其表意。比如，以中共十八大的各省代表人数为例。假若为每一个省（港澳台除外）单独设色，会是这样的效果（注：每张地图点击都可以看大图的，不再说明）：

（图1 单一设色分类）

这样的地图让人不明其意，不知道各个省的代表人数到底几何。因为人眼分辨差异（类别数）的能力是有限的（多于7个类别就有点难了吧）。倘若为之分类，就可以极大地简化数据，显现出数据的空间分布特征、模式，更便于人们使用和分析。

所谓数据分类，就是将数据按照大小排列，并以一定的方法（主观、客观的或统计的，等等），将某一部分归为一类，这样每一个数据都有自己的类别，且仅属于一类。数据分类看似是一个很简单的东西，一般我们做图时选择往往随便选个分类，可能连分类方法都不去看，再找个顺眼的颜色，也不知道这些颜色因何而配的（我也不知道），确定显示觉得ok就行了，不ok就再改改，直到满足你的审美为止。最终可能看上去漂亮，但也就只剩看上去还行了，而缺乏基本的分类依据。比如，各个分类方法的原理是什么？什么分类方法适用于什么数据？ArcGIS为什么选择了Natural Breaks作为默认分类法？这些都是简单的操作背后值得思考的问题。

数据说明

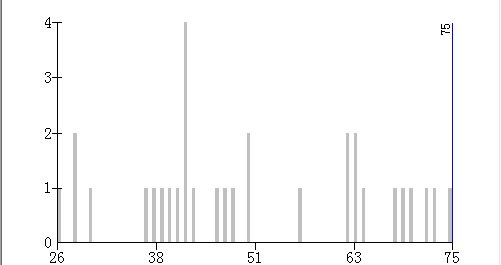
本文将以刚刚胜利结束的中共十八大中各省参会代表人数为数据源，讨论数据分类的问题。本届会议各省代表共计1556人，以下是分布直方图：

（图2 数据分布直方图）

为什么用这个数据？一直觉得，不管是学习还是工作，使用的数据一定要真实，最好还有时效性。真实是一个首要条件。学习中，如果数据真实，才会让自己产生更多的兴趣，有折腾的动力；工作中，只有数据真实，你的工作才有点用处，不然再怎么努力也是自欺欺人。另外，全国各省的矢量数据还是比较容易获得的，这样关联起来就成了本文所用的数据了。至于数据分布是否合适，这就是天命了，该怎么样就怎么样。

常用的分类方法

以ArcGIS提供的六种分类方法为例：Defined Interval、Equal Interval、Quantile、Standard Deviation、Natural Breaks(Jenks)、Geometry Interval（Geometry Interval是Esri自己开发的一种分类法，资料太少，这个就先不讨论），介绍下各种方法的原理、实现以及用途，以前文数据为例。

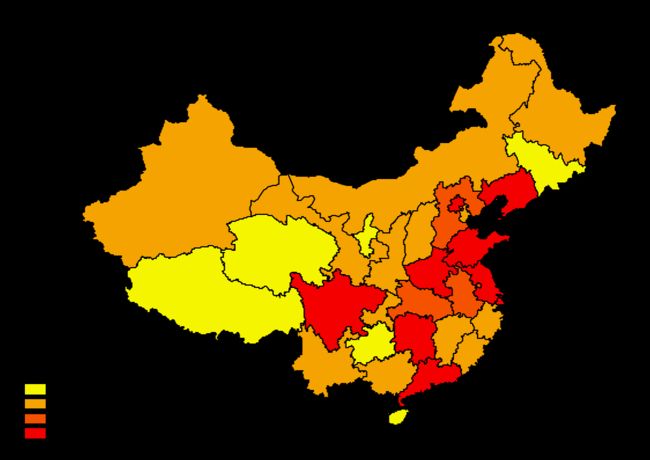
Defined Interval

定义间隔分类。定义一个间隔，比如0～100的数据，定义10为间隔，那么10，20…就是断点，分类数由间隔大小决定。

（图3 Defined Interval分类图，Interval=15）

用Defined Interval分类，提供的信息不多，只能看出不同的省份落在了不同的区间而已，而这个区间的大小没有太大的实际意义。

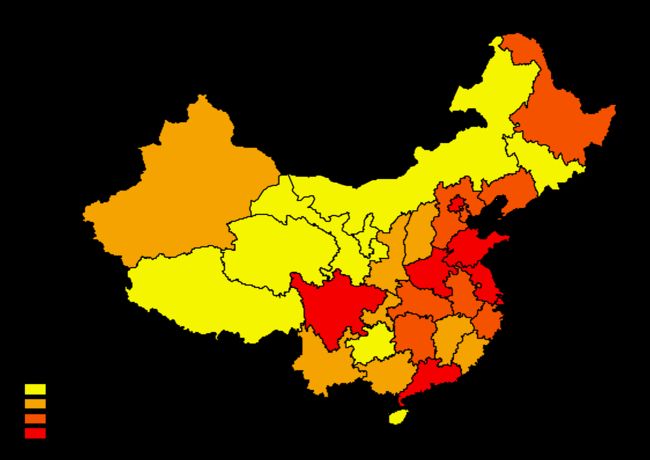
Equal Interval

等距分类。定义一个分类数，比如0～100的数据，分为4类，那么间隔就是25。间隔定了，那就和定义间隔分类的原理一致了。

等距分类和上面的定义间隔分类原理简单，易于计算。比较适合用在温度、成绩和百分比等范围、间隔都为人熟知的数据。但是这两种分类法可能会有“空类”（定义间隔也是的），比如0～100的数据，大部分都在0～50中，剩下的几个在90～100。如果你再按10为间隔去分类，那将会有4个空类！

（图4 Equal Interval分类图）

同样，Equal Interval分类提供的信息也不多。

Quantile

等量分类。又叫分位数分类，每一类的数目一样，这样就不会出现空类了。等量分类适合用于线性分布的数据，比如排名数据。但它不考虑数值大小，很可能将两个大小相近的值分到不同的类别中，也可能数据一样的数据，却分在不同的类中。

（图5 Quantile分类图）

Quantile分类，每一类中的数目是相同的，也就是每一种颜色的省份个数一样，但它忽视了省份之间人数的差异。

Standard Deviation

标准差分类。显然适合正态分布的数据，用于表现与均值相异的程度。但涉及一点点统计知识，普通用户可能不好理解。

（图6 Standard Deviation分类，Interval=1std）

Standard Deviation分类可以看出黄色的省份人数适中（均值），而绿色就偏少了，红色最多。另外，这种分类法的图例与一般的不一样，原因是显而易见的。

Natural Breaks(Jenks)

自然断点分类。一般来说，分类的原则就是差不多的放在一起，分成若干类。统计上可以用方差来衡量，通过计算每类的方差，再计算这些方差之和，用方差和的大小来比较分类的好坏。因而需要计算各种分类的方差和，其值最小的就是最优的分类结果（但并不唯一）。这也是自然断点分类法的原理。另外，当你去看数据的分布时，可以比较明显的发现断裂之处（可以参看前文直方图），这些断裂之处和Natural Breaks方法算出来也是一致的。因而这种分类法很“自然”。

那Jenks又是谁？简单介绍下：

George F. Jenks (1916-1996)，美国制图学家，生于纽约。41年本科毕业后加入陆军航空队，退伍后进入雪城大学深造，在Richard Harrison指导下学习制图。49年博士毕业后获堪萨斯大学教职，设计并执教制图学课程至退休。Jenks发明的Natural Breaks分类法是最常用的数据分类法，也是ArcGIS中的默认分类法。

Natural Breaks算法又有两种：

（1）Jenks-Caspall algorithm(1971)，是Jenks和Caspall发明的算法。原理就如前所述，实现的时候要将每种分类情况都计算一遍，找到方差和最小的那一种，计算量极大。n个数分成k类，就要从n-1个数中找k-1个组合，这个数目是很惊人的。数据量较大时，如果分类又多，以当时的计算机水平根本不能穷举各种可能性。所以当时计算的得到的自然断点是看“运气”的！当然也有一些经验得来的评价指标。

（2）Fisher-Jenks algorithm(1977)，Fisher(1958)发明了一种算法提高计算效率，不需要进行穷举（暂时还没看明白，文献也很少。等我弄明白了，再另写吧）。Jenks将这种方法引入到数据分类中。但后来者几乎只知道Jenks而不知Fisher了，难道是学地理的数学都太差的缘故: P。ArcGIS也是以这个算法为基础改进的，就是说还要更快！开源软件中也有些实现了，后面再说。

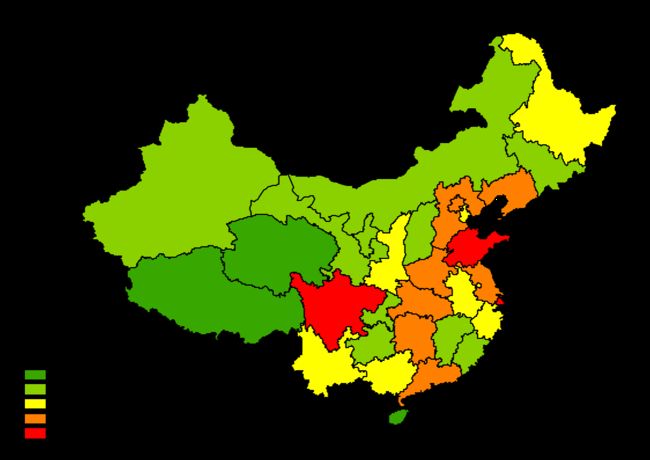
（图7 Natural Breaks分类图）

Natural Breaks分类可以很好地“物以类聚”，类别之间的差异明显，而类内部的差异是很小的，每一类之间都有一个明显的断裂之处。

比较与总结

从直观上看，这份数据用Standard Deviation和Natural Breaks分类的效果较好，它们两个都考虑了数据分布的统计特征。而Equal(Defined) Interval和Quantile，仅仅是两种相对主观的分类法，不管是类间的距离还是类的数目，在这里都没有明确的标准。不像温度这样的数据，长久以来大家都有默认的区间，比如以10度为区间。

这个比较还说明了一点，即相同的数据，用不同分类方法，所表现的效果是截然不同的，特别是偏度很大或很小的数据。idvsolutions曾撰文讨论过，可参考。

另外，如果要表示时序数据的时候，分类一定要确定，不能因为不同时刻不同数据有不同的分类。比如地图汇的这个气温变化例子，做得很好。不过有个小问题，就是图例的区间都是闭合且连续的。即上一个区间的终点和下一个区间的起点相同，那这个间断点到底应该属于哪一类呢？貌似地图汇暂时都是这样的处理。

分类的评价指标

GVF，The Goodness of Variance Fit，暂且叫“方差拟合优度”吧，公式如下：

（公式1 GVF）

其中，SDAM是the Sum of squared Deviations from the Array Mean，即原始数据的方差；SDCM是the Sum of squared Deviations about Class Mean，即每一类方差的和。显然，SDAM是一个常数，而SDCM与分类数k有关。

一定范围内，GVF越大，分类效果越好。SDCM越小，GVF越大，越接近于1。而SDCM随k的增大而大，当k等于n时，SDMC=0，GVF=1。也就是说k越大，GVF越大。但这显然不是说k越大分类效果越好，就如前文提到过的，人的眼睛能识别的类别是有限的，而且也见过了单一设色的效果，很糟糕。

那这个GVF怎么用，又有什么用呢？主要有两种用途：

（1）类数相同，比较方法的优劣

GVF可以用来比较不同的方法，在相同类数情况下，分类效果的优劣。比如，上述几个分类的GVF：

分类方法	GVF
Defined Interval	0.7203
Equal Interval	0.7128
Quantile	0.7271
Natural Breaks	0.8524
Standard Deviation	0.8137

（表1 GVF大小比较图；注：Standard Deviation类数肯定是奇数的，区间为1std时是5；其余分类数均为4）

可见，Natural Breaks明显优于别的分类法，而且任何数据都是这个结果，因为GVF中的SDCM就是Natural Breaks中类方差和嘛。既然Natural Breaks计算出的方差和（SDCM）是最小的，那GVF显然是最大的了。从这个角度来说，Natural Breaks是最优的分类法，ArcGIS将其作为默认分类法也是因为这个原因，有些地方将也称Natural Breaks为Optimal，都显示出了该方法的优越性。

（2）方法相同，比较类数的优劣

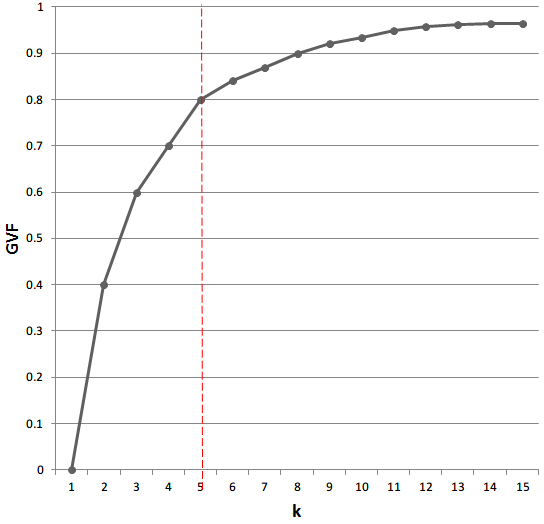
GVF还能用于比较一个方法，不同分类数的分类效果好坏。以k和GVF做图可得：

（图8 GVF变化图）

随着k的增大，GVF曲线变得越来越平缓。特别是在红线处（k=5），曲线变得基本平坦（之前起伏较大，之后起伏较小），k(5)也不是很大，所以可以分为5类。一般来说，GVF>0.7就可以接受了，当然越高越好，但一定要考虑k不能太大。显然，这是一个经验公式，但总比没有好吧。

不分类可以吗？

数据分类的缘起就是因为早年的制图技术不能实现唯一值设色，客观技术的制约导致了数据分类的需求。现在的技术已经完全可以实现，因而有人对数据分类的必要性提出过质疑。但我想数据分类还是必须的，原因前文已述。但如果真的不分类，如何才能更好地表达专题信息？

Prism Map（棱柱图），可以满足这一的需求：

（图9 单一棱柱图）

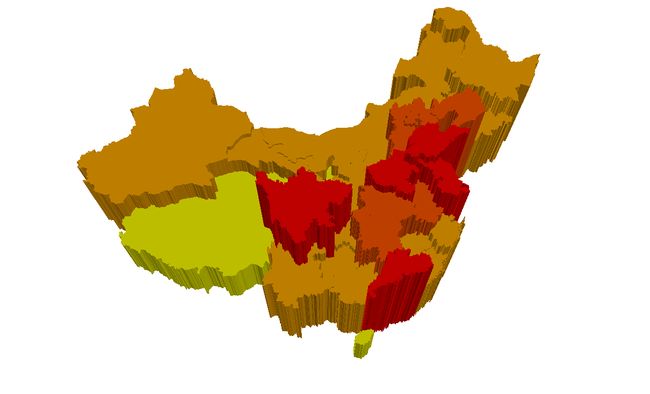
如果再加上自然断点分类，效果就更好了：

（图10 分类棱柱图）

但这不是专题制图的常规手段，比如ArcScene中不能加图例吧。Jenks说可以以Prism Map为标准来评价各种分类的效果，还提出了tabular error、overview error和boundary error三种指标。有兴趣的去翻论文吧: P

由此，可以想到地图投影的各种方法。没有一种投影是完美的，一种投影只能保持一种性质不变。反观数据分类，同样也没有一种分类是完美的，也需要根据不同的需求去选择。空间参考未来或许会归结为没有投影，仅存地理坐标系，所有的显示、分析都基于球面坐标。类似，数据可能也会不需要分类。

更高级的分类法

上述的各种分类法顶多考虑了数据在数轴上的分布，通过统计特征进行分类。而GIS中的数据都是具有空间位置的，如果将空间位置等考虑进去，那分类方法还有很多值得研究的地方。比如空间位置相邻，数值大小也相近，但自然断点分类后却在两个不同的类别中的两个要素，是不是可以考虑分为一类内？类似的分类法（考虑多指标）已经有人研究，目前还没有流行开来，但可以期待是GIS软件中会出现更多的分类方法。

GIS软件中的实现

总结一下各GIS软件中对分类法的实现也是蛮有意思的（以ArcGIS分类法为参考）：

	ArcGIS	SuperMap	MapGIS	QGIS	uDig
Defined Interval	O	O	X	X	X
Equal Interval	O	O	O	O	O
Quantile	O	O	X	O	O
Standard Deviation	O	O	X	O	X
Natural Breaks	O	X	X	O	X
其他	Geometry Interval	对数分段、开方分段	默认提供等距分段	Pretty Breaks	Unique Values

（表2 GIS软件分类法比较）

其中，各测试软件版本号为：ArcGIS 10.1、SuperMap Deskpro 6、MapGIS K9、QGIS 1.8、uDig 1.3.2。

各个厂商对分类的理解不一致的，ArcGIS 不再介绍；超图没有自然断点，另外提供了对数、开方分段；MapGIS默认给数据做等距分段，没有方法选择，只能手动修改；QGIS不提供Defined Interval，矢量支持Natural Breaks，还提供Pretty Breaks（貌似在R中见过）；uDig没有Defined Interval、Quantile以及Natural Breaks，但提供Unique Values（可这不就是不分类吗，这也算一种分类法Orz）。

参考

主要参考了Thematic Cartography and Geovisualization和Cartography: Thematic Map Design，以及若干文献，就不逐一列出了。

代码

我用C#实现了上述提到的分类法，其中Natural Breaks比较“暴力”（穷举），没有用到Fisher的算法，只能有时间再研究了。

using System;
using System.Collections.Generic;
using System.Linq;

namespace Classification
{
    //------------------------ COMMON METHOD
    public static class ClassUtil
    {
        public const double TOLERANCE = 1E-5;

        public enum Distance
        {
            One,
            Half,
            Quarter,
        }

        public static double SquareDeviation(IEnumerable vals)
        {
            var mean = vals.Sum() / vals.Count();
            return vals.Sum(v => (v - mean) * (v - mean)) / vals.Count();
        }

        public static double StandardDeviation(IEnumerable vals)
        {
            return Math.Sqrt(SquareDeviation(vals));
        }

        public static void GetBreaksDetail(double[] vals, double[] breaks, out int[,] range, out double[,] legend)
        {
            var ord_vals = vals.OrderBy(v => v).ToArray();
            var min = ord_vals[0];
            var max = ord_vals[ord_vals.Length - 1];
            var k = breaks.Length + 1;

            range = new int[k, 2];
            legend = new double[k, 2];

            range[0, 0] = 0;
            range[k - 1, 1] = ord_vals.Length - 1;
            legend[0, 0] = min;
            legend[k - 1, 1] = max;
            for (var i = 1; i < k; i++)
            {
                var _break = breaks[i - 1];
                double[] nearest_vals = null;
                int[] nearest_indexes = null;
                findNearestVals(ord_vals, _break, out nearest_indexes, out nearest_vals);
                range[i - 1, 1] = nearest_indexes[0];
                range[i, 0] = nearest_indexes[1];
                legend[i - 1, 1] = nearest_vals[0];
                legend[i, 0] = nearest_vals[1];
            }
        }

        private static void findNearestVals(double[] vals, double obj, out int[] nearest_indexes, out double[] nearest_vals)
        {
            nearest_indexes = new int[2];
            nearest_vals = new double[2];

            for (var i = 0; i < vals.Length; i++) // pre class end
            {
                if (vals[i] - obj >= 0)
                {
                    nearest_indexes[0] = i - 1;
                    nearest_vals[0] = vals[i - 1];
                    break;
                }
            }

            for (var i = vals.Length - 1; i >= 0; i--) // current class begin
            {
                if (vals[i] - obj == 0)
                {
                    nearest_indexes[1] = i;
                    nearest_vals[1] = vals[i];
                    break;
                }
                else
                    if (vals[i] - obj < 0)
                    {
                        nearest_indexes[1] = i + 1;
                        nearest_vals[1] = vals[i + 1];
                        break;
                    }
            }
        }

        public static double GVF(double[] vals, int[,] range) // goodness of viriance fit
        {
            var SDAM = ClassUtil.SquareDeviation(vals); //  the sum of squared deviations from the array mean 

            var SDCM = 0.0d; //  the sum of squared deviations between classes
            var val_list = vals.OrderBy(v => v).ToList();
            for (var i = 0; i < range.GetUpperBound(0) + 1; i++)
            {
                var class_vals = val_list.GetRange(range[i, 0], range[i, 1] - range[i, 0] + 1);
                SDCM += ClassUtil.SquareDeviation(class_vals);
            }

            var GVF = 1 - SDCM / SDAM;
            return GVF;
        }

        public static void PrintLegend(double[,] legend, String method)
        {
            Console.WriteLine(method);
            for (var i = 0; i < legend.GetUpperBound(0) + 1; i++)
            {
                Console.WriteLine(String.Format("{0}~{1}", legend[i, 0], legend[i, 1]));
            }
        }

        public static void PrintGVF(double[] vals, int[,] range)
        {
            Console.WriteLine("GVF: " + ClassUtil.GVF(vals, range));
        }
    }

    //------------------------ DEFINED INTERVAL
    public static class DefinedInterval
    {
        public static double[] GetBreaks(double[] vals, double interval)
        {
            var ord_vals = vals.OrderBy(v => v).ToArray();
            var min = ord_vals[0];
            var max = ord_vals[ord_vals.Length - 1];
            var range = max - min;

            var result = new List();
            var _break = min;
            while (max - (_break + interval) > ClassUtil.TOLERANCE) // the last class interval may be different(arcgis is the first class)
            {
                _break += interval;
                result.Add(_break);
            }

            return result.ToArray();
        }
    }

    //------------------------ EQUAL INTERVAL
    public static class EqualInterval
    {
        public static double[] GetBreaks(double[] vals, int count)
        {
            var result = new List();

            var ord_vals = vals.OrderBy(v => v).ToArray();
            var min = ord_vals[0];
            var max = ord_vals[ord_vals.Length - 1];
            var interval = (max - min) / count;
            var _break = min;
            while (max - (_break + interval) > ClassUtil.TOLERANCE)
            {
                _break += interval;
                result.Add(_break);
            }

            return result.ToArray();
        }
    }

    //------------------------ QUANTILE
    public static class Quantile
    {
        public static double[] GetBreaks(double[] vals, int count)
        {
            var result = new List();

            var ord_vals = vals.OrderBy(v => v).ToArray();
            var min = ord_vals[0];
            var max = ord_vals[ord_vals.Length - 1];

            var class_count = (int)(ord_vals.Length / count);
            var _break = min;

            for (var i = 1; i < count; i++)
            {
                _break = ord_vals[i * class_count];
                result.Add(_break);
            }

            return result.ToArray();
        }
    }

    // STANDARD DEVIATION
    public static class StandardDeviation
    {
        public static double[] GetBreaks(double[] vals, ClassUtil.Distance distance)
        {
            var result = new List();

            var ord_vals = vals.OrderBy(v => v).ToArray();
            var mean = ord_vals.Sum() / ord_vals.Length;
            var min = ord_vals[0];
            var max = ord_vals[ord_vals.Length - 1];
            var std = ClassUtil.StandardDeviation(vals);

            var dist = 0.0d;
            switch (distance)
            {
                case ClassUtil.Distance.One:
                    dist = std;
                    break;
                case ClassUtil.Distance.Half:
                    dist = std / 2;
                    break;
                case ClassUtil.Distance.Quarter:
                    dist = std / 4;
                    break;
                default:
                    break;
            }

            var _break = mean - dist / 2;
            result.Add(_break);
            while (_break - dist - min > ClassUtil.TOLERANCE)
            {
                _break -= dist;
                result.Add(_break);
            }

            result.Reverse();

            _break = mean + dist / 2;
            result.Add(_break);
            while (max - (_break + dist) > ClassUtil.TOLERANCE)
            {
                _break += dist;
                result.Add(_break);
            }

            return result.ToArray();
        }
    }

    // NATURAL BREAKS
    public static class NaturalBreaks
    {
        public static double[] GetBreaks(double[] vals, int count)
        {
            var group_vals = vals.OrderBy(v => v).GroupBy(v => v).ToDictionary(g => g.Key, g => g.ToArray());

            var n = group_vals.Keys.Count;
            var k = count;

            var all_breaks = getAllBreaks(n - 1, k - 1); // combination

            var min_sum_sqd = double.MaxValue;
            int[] optimal_breaks = null;
            foreach (var breaks in all_breaks)
            {
                var break_positions = new List();
                break_positions.Add(0);
                break_positions.AddRange(breaks);
                break_positions.Add(n);

                var sum_sqd = 0.0d;
                for (var i = 0; i < break_positions.Count - 1; i++)
                {
                    var begin = break_positions[i];
                    var gap = break_positions[i + 1] - begin;

                    var class_vals = new List();
                    for (var j = 0; j < gap; j++)
                    {
                        var key_index = begin + j;
                        var key = group_vals.Keys.ElementAt(key_index);
                        var key_vals = group_vals[key];

                        class_vals.AddRange(key_vals);
                    }

                    sum_sqd += ClassUtil.SquareDeviation(class_vals.ToArray());
                }

                if (sum_sqd < min_sum_sqd) // ignore the same min_sum_sqd
                {
                    min_sum_sqd = sum_sqd;
                    optimal_breaks = breaks;
                }
            }

            var result = new List();
            foreach (var _break in optimal_breaks)
            {
                result.Add(group_vals.Keys.ElementAt(_break));
            }

            return result.ToArray();
        }

        private static List getAllBreaks(int n, int k)
        {
            var r = new int[k + 1];
            var rs = new List();
            combination(n, k, r, rs);
            return rs;
        }

        private static void combination(int n, int k, int[] r, List rs)
        {
            for (var i = n; i >= k; i--)
            {
                r[k] = i;
                if (k > 1)
                {
                    combination(i - 1, k - 1, r, rs);
                }
                else
                {
                    rs.Add(r.Skip(1).ToArray());
                }
            }
        }
    }
}

这是测试数据。