HOG（histogram of oriented gradients）特征个人总结

前述

前段时间参加了一项无人飞行器竞赛，用到了HOG+SVM经典算法识别被测物体。赛后系统的查看论文、博客，对HOG特征进行总结。

HOG特征概述

HOG的全称是histogram of oriented gradients，即梯度方向直方图。在2005年，由Dr. Mubarak Shah在CVPR 2005上的论文Histograms of Oriented Gradients for Human Detection 中首次提出。HOG特征作为一种特征描述子，主要用于计算机视觉和图像处理中的物体检测。下面讲一下HOG特征的组成部分。
HOG特征是通过计算和统计图像局部区域的梯度方向直方图来构成的特征。如下图所示，HOG特征提取将图片分成窗口（window）、块（block）、单元（cell）、区间（bin）。其中窗口大小是块的整数倍，块在窗口内以某一固定步长进行滑动；块是单元的整数倍，块刚好可以填满整数倍的单元，并且梯度的计算也在单元内进行；区间是直方图内的横轴的区间，由于HOG特征是以梯度方向为横轴，需要对方向规定角度范围。根据上述论文得到，窗口的大小64x128，块的大小为16x16，步长为8，单元的大小为8x8，区间为9，效果最好。HOG特征算法提取如下。

HOG特征提取

图像预处理

如图所示，首先，我们将图片中的检测目标通过感兴趣区域（ROI）的方式提取出来，然后将ROI的大小缩放为$64\times 128$.然后，我们可以对图像进行伽马校正和灰度化。这两步可做可不做，对实验结果影响不大。其中伽马矫正可以调节图像对比度，减少光照对图像的影响（光照不均和局部阴影），修正过曝或者欠曝的图像。灰度化是将彩色图转换成灰度图，可以直接对彩色图做处理，先对彩色图做通道分离，然后分别对通道计算，采用梯度权值最大的通道作为该像素的梯度权值（即直方图的纵轴变量）。

计算梯度

HOG特征的方向梯度是以cell为单元，如下图a所示为图像中某一cell中的元素P以及其邻域像素值，图b为梯度方向的水平和垂直方向内核，分别用于计算水平梯度和垂直梯度。

a. 区间cell中某一像素	b. 梯度计算的水平和垂直方向内核

先计算像素$P$的水平梯度和垂直梯度，即水平梯度为$P_x=c-a$，垂直梯度为$P_y=d-b$.则每个像素的梯度权值和梯度方向为
$$P=\sqrt{P_x^2+P_y^2}$$
$$\theta =arctan\frac{P_x}{P_y}$$
其中$P$为梯度权值，$\theta$为梯度方向。在这里，我们将梯度方向取绝对值，则梯度方向的范围是0-180度。
由上述可知每个单元（cell）由$8\times 8=64$个像素，每个像素可生成一个Vector（包含梯度权值和梯度方向），即每个单元（cell）可求出64个Vector。
水平梯度和垂直梯度部分的代码实现可以使用OpenCV中的内核大小为1的Sobel算子计算，代码如下：

// C++ gradient calculation. 
// Read image
Mat img = imread("bolt.png");
img.convertTo(img, CV_32F, 1/255.0);

// Calculate gradients gx, gy
Mat gx, gy; 
Sobel(img, gx, CV_32F, 1, 0, 1);
Sobel(img, gy, CV_32F, 0, 1, 1);

# Python gradient calculation 

# Read image
im = cv2.imread('bolt.png')
im = np.float32(im) / 255.0

# Calculate gradient 
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

梯度方向和梯度权值部分的代码如下

// C++ Calculate gradient magnitude and direction (in degrees)
Mat mag, angle; 
cartToPolar(gx, gy, mag, angle, 1); 

# Python Calculate gradient magnitude and direction ( in degrees ) 
mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

计算区间（cell）直方图

上述已经将单元（cell）内的像素的梯度求出来了，现在将计算单元（cell）的梯度直方图。如下图所示，左边的图为被测目标图片。中间的图为被测目标图中的某个单元（cell），图中的蓝色箭头表示对应像素点的梯度，共有64个箭头，其中箭头方向表示梯度方向，箭头长度表示梯度权值。右边的图则是将单元（cell）中的梯度方向/梯度权值分为两个图。

每个单元（cell）都有$8\times 8=64$个Vector，如下图所示，将他们分成梯度方向/梯度权值两个部分，每部分有64个值。梯度方向的范围为0-180度，因为我们已经将梯度方向分为9个区间（bin），即$0,20,40,60,80,100,120,140,160$,所以我们可以将64个梯度权值分配到9个区间内。则64个Vector便可以变成9个Vector，大大降低了计算量，同时因为是局部梯度计算，增强了对环境光的抗干扰能力。

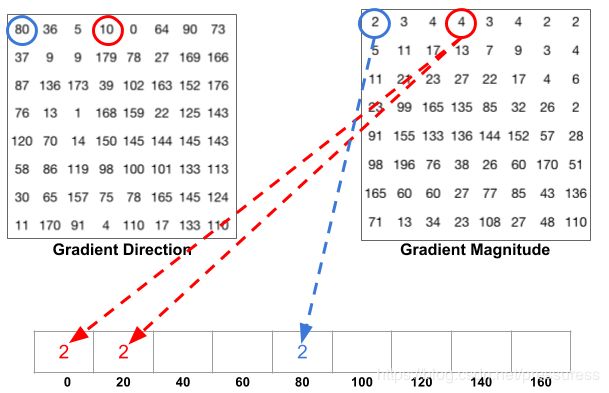
其中左上图是$8\times 8$的梯度方向值，右上图是$8\times 8$的梯度权值，下图是9个区间（bins）。上图两个蓝圈对应的为左上角第一个像素的方向和权值，因为方向为80，所以将2放入80这个区间（bin）内。两个红圈表示第一行第四列的像素的方向和权值，因为方向为10，距离区间（bin）0和20的距离分别为10、10.因此区间（0）内的值增加$\frac{10}{20}\times 4=2$,区间（bin）20内的值增加$\frac{10}{20}\times 4=2$。那么统计完64个点后，每个bin就会得到一个数值，可以得到如下图所示的一个直方图。

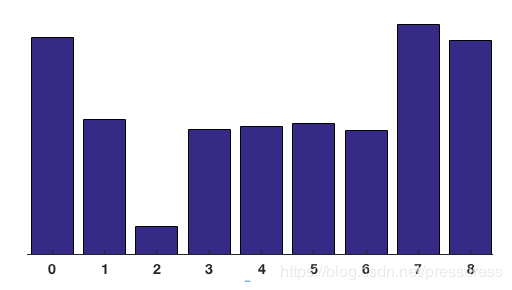
归一化块（block）

归一化就是将向量的每个值除以向量的模长，比如一个三维点坐标为[128, 64, 32],其模长为$\sqrt{128^2+64^2+32^2}=146.64$,则归一化后的值为$[\frac{128}{146.64},\frac{64}{146.64},\frac{32}{146.64}]=[0.87,0.43,0.22]$.

归一化块（block）可以降低计算量，并减轻光照对HOG特征提取的影响。如图所示为块（block）在窗口（window）下的遍历方式。上面已经得到单元（cell）的梯度，即一个单元有9个Vector，而一个块（block）包含4个单元（cell），即$9\times 4=36$个Vector，然后对这36个Vector做归一化即可。以此类推，便可以将所有块（block）归一化。

计算HOG特征向量

每个$16\times 16$块（block）有36个Vector，则大小为$64\times 128$的窗口（window），块（block）的步长为8，总共有$7\times 15=105$个块（block）。即一个窗口（window）有$7\times 15\times 36=3780$个Vector。

可视化HOG特征

将窗口（window）下的所有梯度如上图所示表示出来，图中红色线段表示每个单元（cell）的梯度（梯度方向/梯度权值）。

结论

HOG的优点：

• 核心思想是所检测的局部物体外形能够被梯度或边缘方向的分布所描述，HOG能较好地捕捉局部形状信息，对几何和光学变化都有很好的不变性；
• HOG是在密集采样的图像块中求取的，在计算得到的HOG特征向量中隐含了该块与检测窗口之间的空间位置关系。
  矩形HOG和SIFT有些相似的地方，关于SIFT具体看这篇博文SIFT特征提取分析
  HOG的缺陷：
• 很难处理遮挡问题，人体姿势动作幅度过大或物体方向改变也不易检测（这个问题后来在DPM中采用可变形部件模型的方法得到了改善）；
• 跟SIFT相比，HOG没有选取主方向，也没有旋转梯度方向直方图，因而本身不具有旋转不变性（较大的方向变化），其旋转不变性是通过采用不同旋转方向的训练样本来实现的；
• 跟SIFT相比，HOG本身不具有尺度不变性，其尺度不变性是通过缩放检测窗口图像的大小来实现的；
• 此外，由于梯度的性质，HOG对噪点相当敏感，在实际应用中，在Block和Cell划分之后，对于得到各个像区域中，有时候还会做一次高斯平滑去除噪点。

参考

Histograms of Oriented Gradients for Human Detection 论文
Histograms of Oriented Gradients (HOG) Video
Histogram of Oriented Gradients Learn OpenCV
https://zhuanlan.zhihu.com/p/40960756 知乎
HOG特征（Histogram of Gradient）总结 CSDN