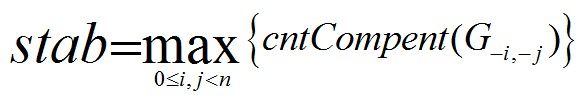CCSU团队训练赛 ( A 数学 B tarjan F dij G dp H 线段树 )
题目链接
设的虚拟,可能进不去,每个题有给原题链接。算作是私人题解吧。
A - Play the Dice HDU - 4586
There is a dice with n sides, which are numbered from 1,2,...,n and have the equal possibility to show up when one rolls a dice. Each side has an integer ai on it. Now here is a game that you can roll this dice once, if the i-th side is up, you will get ai yuan. What's more, some sids of this dice are colored with a special different color. If you turn this side up, you will get once more chance to roll the dice. When you roll the dice for the second time, you still have the opportunity to win money and rolling chance. Now you need to calculate the expectations of money that we get after playing the game once.
题意:n面的色子,m面特殊面,进行一次掷色子,概率期望为p 第二次 m/n*p 第三次 m/n*m/n*p 。。。。求和就是等比求和公式
a1=m/n
分三种情况讨论:
1、当a1为0时,输出0.00;
2、当a1等于1时,说明可以无限的投掷下去,输出inf;
3、当a1< 1时,N无穷大时,1-q^N 的q^N 无限接近于0,那么原式变为a1/(1-q)。
#include
using namespace std;
const int N=2e2+10;
int n,m,vis[N],a[N];
int sum,cnt;
double p,q;
const double eps=1e-6;
int main()
{
while(~scanf("%d",&n))
{
sum = 0,cnt = 0;
memset(vis,0,sizeof(vis));
for(int i = 1; i <= n; i++)
{
scanf("%d",&a[i]);
sum += a[i];
}
p = (sum*1.0)/n;
scanf("%d",&m);
int x;
for(int i = 1; i <= m; i++)
{
cin >> x;
if(vis[x]) continue;
vis[x] = 1;
cnt++;
}
q = (1.0*cnt)/n;
if(fabs(p) < eps) puts("0.00");
else if(fabs(q-1) < eps) puts("inf");
else printf("%.2lf\n",p/(1-q));
}
return 0;
} B - TWO NODES HDU - 4587
Suppose that G is an undirected graph, and the value of stab is defined as follows:
Among the expression,G -i, -j is the remainder after removing node i, node j and all edges that are directly relevant to the previous two nodes. cntCompent is the number of connected components of X independently.
Thus, given a certain undirected graph G, you are supposed to calculating the value of stab.题意:去除两个点 使得剩下的图 联通块的个数 最大,
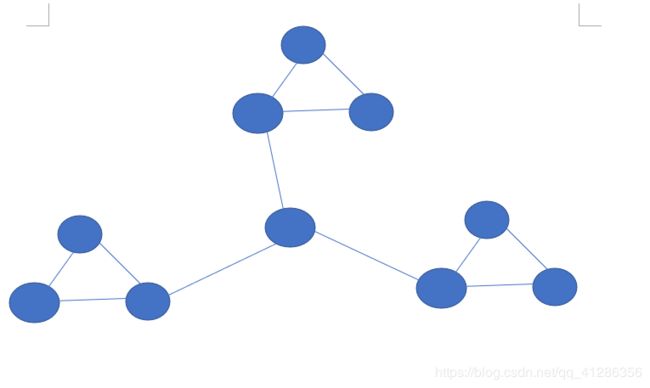
做法:百度有个人的博客刷屏了 他写的题意是强联通块的个数,如果是强连通块的话 下面这个样例答案应该是4 而他的代码是3
因为两个点只有一条线相连,那么这两个点属于不同的强连通
如果只是去除一个点的话 好做,用tarjan 计算一下 去除这个点时附近产生的 连通块的个数 即可
如果是去除两个点,枚举去除的那个点,然后再套用tarjan。
代码就懒的打了,贴的别人的
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=5010;
struct data
{
int to,next;
} tu[N*N];
int head[N],low[N],dfn[N];///dfn[]记录某个点被访问到的次数,low[]记录某个点或其子树回边的最小步数的点
int cut[N];///是否为割点且该点连接边的数量
int ip;
int step,rt_son,scc_cnt;
void init()
{
ip=0;
memset(head,-1,sizeof(head));
}
void add(int u,int v)
{
tu[ip].to=v,tu[ip].next=head[u],head[u]=ip++;
}
void tarjan(int u,int del)
{
//cout<=dfn[u])
cut[u]++;
}
else
low[u]=min(low[u],dfn[to]);
}
}
void solve(int n)
{
int ans=0;
for(int j=1; j<=n; j++)
{
memset(dfn, 0, sizeof(dfn));
for(int i=1; i<=n; i++)
cut[i]=1;
step = 1;
int sum=0;
for (int i = 1; i <=n; i++)
if (i!=j&&!dfn[i])
{
sum++;//联通块的个数
cut[i]=0;
tarjan(i,j);
}
for(int i=1; i<=n; i++)
if(i!=j)
{
//if(sum+cut[i]-1)
ans=max(ans,sum+cut[i]-1);
}
}
printf("%d\n",ans);
}
int main()
{
int m,n;
while(~scanf("%d%d",&n,&m))
{
init();
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
a++,b++;
add(a,b);
add(b,a);
}
solve(n);
}
return 0;
}
/*
10 12
0 1
1 2
2 3
3 1
0 4
4 5
5 6
6 4
0 7
7 8
8 9
9 7
*/ F - Shortest Subchain URAL - 1651
题意:给你一条单链,求此单链上 从起点出发到达终点最短的一条子链,意思就是说可能会有环,那么这个环去掉即可。
做法:对于 这条链上 前后出现了相同的点时 连一条长度为0 的边,其余的按照链上的顺序连权值为1的边,跑一次最短路,接着输出最短路就好了。很坑的是,题意没告诉你是多组输入,结果我单组输入 wa到炸
#pragma GCC optimize(2)
#include
#define ll long long
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e5+10;
vector >G[N];
int n,a[N],vis[10010];
int dis[N],fa[N],ans[N];
struct node
{
int u,w;
bool operator <(const node &o) const
{
return w>o.w;
}
};
void bfs()
{
priority_queueque;
rep(i,1,n) dis[i]=1e9;
dis[1]=0;
que.push({1,dis[1]});
while(que.size()){
node now=que.top();que.pop();
for(auto it:G[now.u]){
if(dis[it.first]>dis[now.u]+it.second){
dis[it.first]=dis[now.u]+it.second;
fa[it.first]=now.u;
que.push({it.first,dis[it.first]});
}
}
}
}
int main()
{
while(~scanf("%d",&n))
{
rep(i,1,n) G[i].clear(),fa[i]=0;
memset(vis,0,sizeof(vis));
rep(i,1,n) a[i]=read();
vis[a[1]]=1;
for(int i=2;i<=n;++i){
if(vis[a[i]]!=0) G[vis[a[i]]].push_back({i,0});
vis[a[i]]=i;
G[i-1].push_back({i,1});
}
bfs();
//rep(i,1,n) printf("i:%d dis:%d\n",i,dis[i]);
//int len=0;
int now=n;
stacksta;
while(now!=1){sta.push(now);now=fa[now];}
sta.push(1);
int pre=0;
while(sta.size())
{
if(a[sta.top()]!=pre) printf("%d ",a[sta.top()]);
pre=a[sta.top()];
sta.pop();
}
puts("");
}
}
/*
9
1 2 7 3 2 8 4 8 5
10
1 2 3 4 5 2 4 6 7 5
1 2 3 4 5
7
1 2 3 1 4 2 5
1 2 5
*/
G - Sum of Digits URAL - 1658
Petka thought of a positive integer n and reported to Chapaev the sum of its digits and the sum of its squared digits. Chapaev scratched his head and said: “Well, Petka, I won't find just your number, but I can find the smallest fitting number.” Can you do the same?
题意:构造n位 每位和为s1 每位的平方和为2的最小的数。
做法:简单dp:dp[i][s1][s2] 第i为为dp[i][s1][s2] 和为s1 平方和为s2 。内存爆炸,简化一下,发现每个状态的dp 是唯一的。
于是去掉一维 dp[s1][s2] 用ans[s1][s2]保存到达s1、s2 需要填的数(1~9)
t组,预处理一下,然后逆着输出路径即可。
#pragma GCC optimize(2)
#include
#define ll long long
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
int dp[901][8101],ans[901][8101];
void init()
{
for(int i=0;i<=900;++i){
for(int j=0;j<=8100;++j) dp[i][j]=inf;
}
dp[0][0]=0;
for(int i=1;i<=900;++i){
for(int j=1;j<=8100&&j<=i*i;++j){
for(int k=1;k<=9;++k){
if(i-k<0||j-k*k<0) break;
if(i-k>j-k*k) break;
if(dp[i][j]>dp[i-k][j-k*k]+1){
dp[i][j]=dp[i-k][j-k*k]+1;
ans[i][j]=k;
}
}
}
}
}
int main()
{
init();
int _=read();while(_--)
{
int n=read(),m=read();
if(n>900||m>8100){
puts("No solution");
continue;
}
if(dp[n][m]>100){
puts("No solution");
continue;
}
vectorres;
while(n&&m){
int now=ans[n][m];
//printf("n:%d m:%d now:%d\n",n,m,now);
res.push_back(ans[n][m]);
n-=now,m-=now*now;
}
for(int v:res) printf("%d",v);
puts("");
}
}
/*
4
9 81
12 9
6 10
7 9
*/ H - Billionaires URAL - 1650
题意:给定n个富豪的身价,以及最初始 所在的城市,然后m个富豪外出旅游的计划表。问每个城市 富豪的身价之和严格大于其他城市 时的天数。
做法:怎么URAL的题都这样,上一个题没讲多组输入,这个题又搞隐性题意,两个城市的身价之和 相同时 不贡献答案。
被这个不贡献答案卡了一个 小时。
让我想起了高中英语题
题面:His mother was a nurse
题目:Is his mother a nurse?
答案是错的,因为题面 用的是过去式,题面问的现在时。这题 我们班英语130分的学霸还做错了。。。真的就是英语不好很吃亏(母语为英语的国家真好)。
复杂模拟,几个map 保存 富豪对应的身价,城市对应身价和 保存最大身价和的个数。线段树搞搞就好了。
#pragma GCC optimize(2)
#include
#define ll long long
#define maxn 1005
#define inf 1e9
#define pb push_back
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
const int N=1e5+10;
int n,m,cnt,q;
mapname_city;
string tid[N];
mapvis;
setst;
mapcity_num,name_num,ans;
mapnum;
ll x;
struct node
{
string s;
ll num;
};
int t[N];
string name[N],city[N];
struct tree
{
string city;
ll x;
}mx[4*N];
tree Max(tree a,tree b)
{
if(a.x>b.x) return a;
return b;
}
void build(int id,int l,int r)
{
if(l==r){
mx[id].city=tid[l];
mx[id].x=city_num[tid[l]];
num[mx[id].x]++;
return ;
}
int mid=l+r>>1;
build(id<<1,l,mid);
build(id<<1|1,mid+1,r);
mx[id]=Max(mx[id<<1],mx[id<<1|1]);
}
void up(int id,int l,int r,int pos,ll val)
{
if(l==r){
num[mx[id].x]--;
mx[id].x+=val;
num[mx[id].x]++;
return ;
}
int mid=l+r>>1;
if(pos<=mid) up(id<<1,l,mid,pos,val);
else up(id<<1|1,mid+1,r,pos,val);
mx[id]=Max(mx[id<<1],mx[id<<1|1]);
}
bool cmp(node a,node b)
{
return a.s>s1>>s2>>x;
name_city[s1]=s2;
name_num[s1]=x;
st.insert(s2);
city_num[s2]+=x;
}
m=read(),q=read();
rep(i,1,q)
{
t[i]=read();
cin>>name[i]>>city[i];
st.insert(city[i]);
}
cnt=st.size();
for(int i=1;i<=cnt;++i) {
tid[i]=*st.begin();
vis[*st.begin()]=i;
st.erase(st.begin());
}
build(1,1,cnt);
tree tmp=mx[1];
int pre=0;
rep(i,1,q)
{
tree tmp=mx[1];
if(num[tmp.x]==1) ans[tmp.city]+=t[i]-pre;
ll val=name_num[name[i]];
up(1,1,cnt,vis[name_city[name[i]]],-val);
name_city[name[i]]=city[i];
up(1,1,cnt,vis[city[i]],val);
pre=t[i];
}
if(m>=pre){
tree tmp=mx[1];
if(num[tmp.x]==1) ans[tmp.city]+=m-pre;
}
for(auto now:ans) if(now.second)cout<