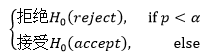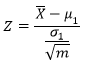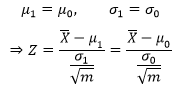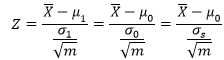概率统计22——假设检验理论(1)
我们可以根据经验或统计量对一些事情做出断言,问题是,如何判断这个断言的合理性?假设检验为我们提供了一种利用样本检验断言是否可靠的方法,能够让我们通过已有的证据验证断言是经过缜密的运算,还是毫无根据的瞎猜。
假设检验的背景
某个机器元件的质量标准是功率,功率越大越好,这个元件影响到公司的核心竞争力。技术组在攻克了重重难题后宣称有了重大突破。总经理非常高兴,宣布批量试制。然而改进后的数据却并不那么漂亮,功率均值从原来的600mW提升到603mW,仅仅提升了0.5%,这让总经理大为光火,立即召集技术组开会。
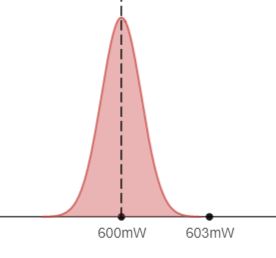
0.5%看起来确实没什么太明显的提升。面对面色铁青的总经理,技术部拿出了改进前的功率分布:
这是个很陡峭的分布曲线,暗示着这个元件的功率控制得十分精细,或者说功率的波动很小,3mW的波动已经相当于“基因突变”了。这样看来,0.5%的提升确实算得上是重大改进。
某个软件公司用每千行的bug数量衡量软件的质量(这里不讨论这种方法是否合理),多年来也做过了很多项目,平均bug率是5.5‰,即每千行代码5.5个bug,勉强达到CMM2的标准。
最近公司全面实施了新的开发方法,发现新项目的bug率降低到4.5‰,这可是降低了18%!于是QA部门的老大在年会上对着分布图激动地宣布,公司软件质量从此迈上了新台阶。
程序员们瞟了一眼分布图,露出了谜之微笑。
上面两个故事告诉我们,在质量改善的过程中,质量提升的百分比并不能作为有效性的唯一依据,0.5%可能是重大提升,18%也可能根本说明不了问题。检验的依据是,改善后是否在改善前总体正常波动的范围内。如果在正常波动范围内,则可以认为并没有什么改善,否则认为有显著改善。这个显著性具体如何判断呢?
显著性水平与置信水平
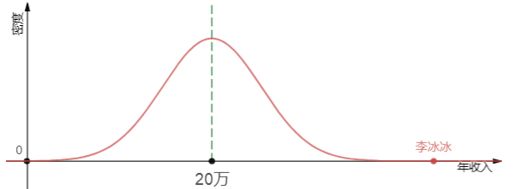
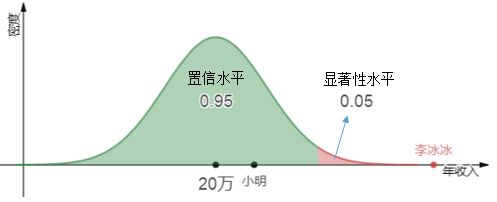
假设下图是哈尔滨市民年收入的概率分布:
大多数人都在20万附近徘徊。
恰好李冰冰出生于哈尔滨市,不小心把她也统计进去了。大明星的收入肯定比普通市民多得多。
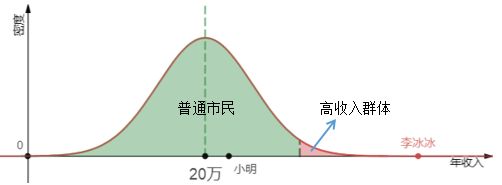
李冰冰明显和普通市民不是一伙的,她的年收入显著高于绝大多数市民,早已跨过了高收入的门坎。某个人的收入落在高收入群体的概率就是显著性水平(Significant Level)。
小明的年收入是25万,和大多数人差不多,我们相信小明是一名普通市民的概率还是比较高的,这个概率就是置信水平(Confidenct Level)。
高收入群体占了总体的多大比例呢?也就是显著性水平应该如何取值?
第一个回答这个问题的人是罗纳德・艾尔默・费舍尔(RonaldAylmerFisher)。
费舍尔(1890 - 1962)是英国统计学家、生物进化学家、数学家、遗传学家和优生学家。是现代统计科学的奠基人之一。著名的F分布就是费舍尔提出的,并以其姓氏的第一个字母命名。
费舍尔提出0.05显著性水平,至于为何要选择0.05,老头在《研究工作者的统计方法》(Statistical Methods for Research Workers)中做过长篇大论,网上有一篇文章叫“Why P=0.05?”(http://www.jerrydallal.com/lhsp/p05.htm),很值得看一下。
现在我们用显著性水平和置信水平去看待哈尔滨市民年收入的问题:
单侧大于显著性
高收入群体在曲线右侧,是“单侧大于”显著性,表示一个人属于高收入群体的概率是0.05,李冰冰明显属于这一侧。相对的,一个人不属于高收入群体的概率是0.95。
现在要判断一个人是否属于低收入群体,此时应当使用“单侧小于”显著性。小明隔壁正好住着一个叫王二的游手好闲的邻居,每个月都等着领政府的救济金混日子,年收入自然很低,绝大多数人都不愿意和他为伍。这类人游手好闲群体在曲线左侧的0.05部分:
单侧小于显著性
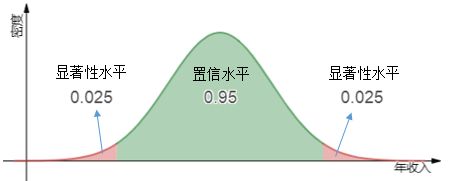
除此之外,还有双侧显著性。按照费舍尔的0.05显著性水平理论,双侧检验时要在总体分布的两端各设定一个临界点,临界点以外,两端阴影部分的面积比率各为0.025,表示超低收入群体和高收入群体一样稀少:
有人说我显著性水平不用0.05行不行?当然没问题,具体怎么设定完全取决于实际问题,0.05只是一个常用的取值。如果想检验得严一点,显著性水平要相应放低,比如0.01;如果宽松一点,显著性水平可以稍高一点,比如0.1,此时你也要同时承担置信水平下降的后果。
有了显著性水平后和置信水平后,就可以从直观上回应总经理的愤怒并理解程序员们的谜之微笑,但我们仍然缺少一些理论知识。检验理论究竟蕴含着怎样的逻辑呢?
假设检验的逻辑
我一直很喜欢打乒乓球,一个好友和我从小学一直打到大学毕业,基本上旗鼓相当。工作之后,我天天苦练球技,自认为如果再次交手一定比他更强。年假回家,我俩又一次站在球台边,并以15局为限,看看时隔多日之后谁更胜一筹。
结果是我5胜10败。
由于几乎每一局都是苦战,所以我并不服气,认为这纯属偶然,如果再打一次,结果完全不可预估。我的理由是:抛15次硬币,10次正面朝上完全有可能。对方则是持否定态度,认为这绝对是实力的差距。
我们二人的争论包含了两种截然相反的假设:
我的假设,H0:双方势均力敌,获胜的概率都是0.5。
朋友的假设,H1:这个结果表明实力的差距,他的获胜的概率大于0.5。
从朋友的立场来看,他想要证明自己是对的,因此把我的H0假设看成原假设(或者叫待验假设、虚无假设),也是他想要驳斥的假设。H1是H0的备择假设(或者叫对立假设、备选假设),是他试图肯定的假设。他的证明逻辑是:如果H0成立,那么出现H1这样的数据的概率将小于α,这个概率用p表示,称为p值(p-value),作为阈值的α是上一节的显著性水平,取α=0.05。用p值是否大于α作为判断依据:
这有点类似于反证法,如果无法直接证明H0是错的,就转换策略,暂且相信H0是对的, 这种情况下出现H1的概率将小于0.05。这种小概率事件应该不容易在抽样中出现,但现在偏偏出现了,是个强有力的反驳证据,所有应当转而相信H1。
现在来计算一下p值。按照原假设H0,我们二人实力相当,每一场比赛的胜率都相等。假设每场比赛都是独立的,用随机变量X表示朋友获胜的总数,那么X符合总数是15,胜率是0.5的二项分布X~B(15, 0.5),p值是:
可以用计算机直接计算:
from scipy import stats c = stats.binom.cdf(10 - 1, n=15, p=0.5) # X~B(n, p)的累积分布 p = 1 - c
结果p ≈ 0.151 > 0.05,看起来是我赢了,应该相信H0。
朋友当然不会满意这个结果,他反驳的理由是样本数量太小,并不能反应真正的胜败分布。于是他提出增加比赛次数,重新打100局。我欣然接受。
几天后终于决出了结果,我38胜62败。
还是沿用之前的原假设和备择假设,用随机变量X表示朋友获胜的总数,这次的p值是:
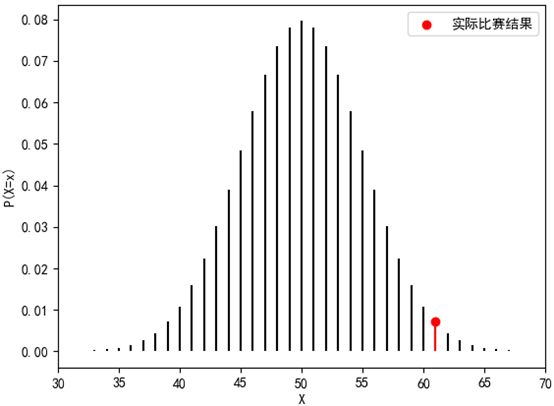
![]()
p值小于显著性水平,因此应当拒绝承认原假设H0,接受对立假设H1,从分布图上能够更清晰地看出这一结论。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
n, p = 100, 0.5
x = 62 # 获胜次数
c = stats.binom.cdf(x - 1, n=n, p=p) # X~B(n, p)的累积分布, P(X <= x-1)
p_value = 1 - c
print(p_value)
xs = np.arange(0, n + 1)
ys = stats.binom.pmf(xs, n=n, p=p) # X~B(n, p)
plt.vlines(xs, ymin=0, ymax=ys)
plt.vlines(xs[x - 1], ymin=0, ymax=ys[x - 1], colors='r')
plt.scatter(xs[x - 1], ys[x - 1], c='r', label='实际比赛结果')
plt.xlim((30, 70))
plt.xlabel('X')
plt.ylabel('P(X=x)')
plt.legend(loc='upper right')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.show()
这次的样本较大,证据要比之前充分得多,所以我应当承认这次的失利绝非偶然。
值得注意的是,假设检验无法并不能给出绝对的证明,仅仅是用小概率事件作为证据,对原假设进行驳斥。基于这个原因,我依然不服气,提出再打100局。当然,朋友也坚决予以否定——1局也不行。
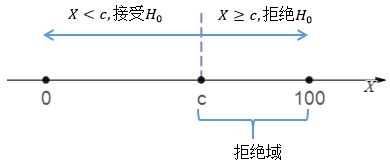
临界值
38胜62败的战绩为驳斥H0提供了强有力的证据,我现在想要知道的是,到底胜多少局才能不被驳斥?也就是0.95置信水平和0.05显著性水平的临界点应该在什么位置?
以c为临界点,将置信水平和显著性水平分隔开来,c的值称为临界值。用X表示朋友获胜的数量,如果P(X ≥ c) = 1 – P(X < c) ≤ α,说明样本位于拒绝域中,应该转而相信备择假设H1。
直接计算c值不太容易,需要使用分布的反函数,幸好可以通过计算机直接计算:
c = stats.binom.ppf(0.95, 100, 0.5) # 当P(X <= c) = 0.95时的c值
结果c=58,这意味着如果我输掉58局以上,就应该属于实力的差距。
假设检验与点估计
我们回到改善机器元件的故事,从抽样分布的角度去看假设检验。
已知元件改善前的功率服从均值为μ0,方差为σ02的正态分布,以下是总经理和技术组的观点。
总经理:技术组纯粹是在说瞎话,质量毫无提升。
技术组:质量得到了极大的改善。
设改善后的总体均值是μ1,方差是σ1,现在用假设检验的逻辑翻译一下:
总经理,原假设H0:改善前与改善后是同一个正态分布,μ0=μ1、σ0=σ1。
技术组,备择假设H1:改善前与改善后是不同的正态分布,μ0 < μ1。
公司用新技术制造了大量元件,从中多次抽取容量是m(m≥30)的样本并计算出均值。根据中心极限定理,样本均值的抽样分布服从均值为总体均值,方差为总体方差1/m的正态分布:
对样本均值进行标准化处理:
按照原假设H0:
根据大数定律和点估计理论,样本标准差σs是总体标准差的合理估计量:
假设元件原来的功率均值是600mW,技术改进后抽取了30个样本进行对比,测得样本的功率均值是603mW,标准差是6。代入后可以求得具体的Z值:
Z服从均值为0方差为1的标准正态分布,可以通过查表求得临界值:
或者直接使用下面的代码计算:
stats.norm.ppf(0.95, 0, 1) # 1.6448536269514722
z>c,z落入了拒绝域,因此应当拒绝相信H0,原假设不成立,技术组的观点才是正确的。
接下来是非常绕的第一类错误和第二类错误(待续)。
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”
![]()