列联表篇之二:四格表的分析
转载出处:https://zhuanlan.zhihu.com/p/27312651
在列联表中,二维表是最基础的一类表,在二维表中,四格表是最基础的一类表。
四格表的基本形式在《经典比较篇之十一:小样本的比率比较怎么做?》中已经介绍,这里在把表贴出来。
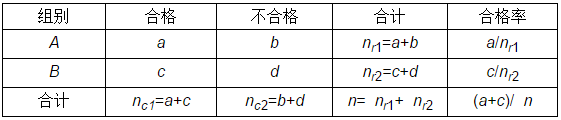
下面针对表格数据的各种不同形式来介绍相应的分析方法。
基本四格表的分析方法
1.正态近似
基本四格表其实是两个比率(就是上表的最后一列)的比较,当比率满足条件np和n(1-p)均大于5时,可以采用正态近似来分析。这个大家都很熟悉了,本文不再涉及。
2.卡方检验
卡方检验的原理上一篇已经介绍过了,见《列联表篇之一:双向无序列联表的分析》。对于四格表来说,有一个专用的公式计算卡方值:
这个公式不再需要计算期望频数了,也不难记,放在这里大家参考着用。
3.卡方检验的校正公式
四格表中的数据不是连续的,因此计算出的卡方值也不是连续的,但分布是连续的。当自由度特别小,尤其是四格表这样只有1的时候,计算出的卡方值偏小,假阳性的概率增大。为此,美国统计学家F.Yates1934年提出了一个计算卡方值的连续性校正公式:
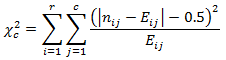
特别的,对于四格表

4.Fisher精确检验
这是一种在小样本情况下的检验方法,对于四格表来说,它运用超几何分布做检验,具体方法和步骤见《经典比较篇之十一:小样本的比率比较怎么做?》。对于大于四格表的列联表,当样本量比较小时,尤其是期望频数小于5的格子超过20%时,也需要采用Fisher精确检验,不过其方法比较复杂,需要借助软件来计算。
5.方法的选择
在孙振球教授的《医学统计学》p.114,介绍了四格表的卡方检验的三个选择原则:
(1)当n≥40且所有的E≥5(也就是a、b、c、d对应的卡方分布的理论频数),可以用卡方检验的基本公式,但当p≈α时,改用Fisher精确检验。
(2)当n≥40但有1≤E<5时,用卡方检验的校正公式,或改用Fisher精确检验。
(3)当n<40,或E<1时,用四格表的Fisher精确检验。
当然,现在统计软件已经功能非常完善了,我认为不管表格中的数据属于哪种情况,直接用Fisher精确检验总会相对准确一些。个人之见,仅供参考。
配对四格表的卡方检验
熟悉经典比较的都知道有配对t检验,在列联表中也有配对的列联表。与配对t检验类似,配对列联表也要求样本保持不变,如可以是部件加工前和加工后的比较,也可以是两种不同的评价方法的对比。表格可以进一步写成这样:

针对配对的四格表,有两种分析方法可以选择,即Mcnemar检验和Kappa检验。前者关注的是差异,后者关注的是一致性。
1.Mcnemar检验
a和d代表结果的一致性,b和c代表结果产生的变化。在Mcnemar检验中,原假设是对样本所施加的处理没有显著效应,也就是发生不同方向变化的可能性是一样的,有多少“-+”,就应该有多少“+-”,即b=c,如果两者差异很大,则说明两种不同的处理有显著的差异,或一种处理的前后状态存在显著差异。
从另一个角度来说,Mcnemar的原假设是边缘概率相等,即

因此Mcnemar检验的假设就可以写成

以此建立的检验统计量为:
从统计量服从自由度为1的分布。
例1:某公司计划引入六西格玛管理,为此选取100员工,在实施六西格玛战略宣讲前后,就引入六西格玛的必要性进行调查,调查结果如下表。问宣讲前后员工的态度有变化吗?

假设就不写了,大家都知道怎么写。计算出的卡方值为:
在α=0.05时,自由度为1的卡方检验临界值为3.84,因此我们拒绝原假设,认为宣讲前后员工的态度有显著变化。
根据孙振球教授的说法,当b+c<40时,检验统计量需要加以校正,即
有的资料中指出当b+c<25时,采用卡方检验会出现较大的偏差,此时需要采用二项分布的精确检验。Mcnemar检验就变成了单比率检验,假设变成

其中n=b+c。单比率检验在《经典比较篇之十一:小样本的比率比较怎么做?》中有介绍,这里不再赘述。
Mcnemar检验与a和d两个格子的值无关,当这两个值很大时,即使检验结果显著,其实际意义也不是很大。因此我们需要考虑一致性的问题,这就需要Kappa检验。
2. Kappa检验
看到Kappa检验,熟悉测量系统分析的人马上就会想起来,在属性数据测量系统分析中,大量采用Kappa值来度量测量结果的一致性。在马逢时教授《六西格玛管理统计指南》p.399-402对此有详细介绍。
Kappa检验由Cohen于1960年提出,因此又称为Cohen'sKappa。它考虑的是实际的结果是不是瞎猜的结果,比如一个新员工对检验标准不了解,但也能蒙对一部分。而Kappa值就是对此的衡量,其公式为:
其中
为实际一致的比率,而
为期望的一致率,即蒙对的比率。
Kappa取值从-1~+1。-1代表完全不一致(a=d=0且b=c);+1代表完全一致(b=c=0);0表示结果纯粹是瞎蒙的;负值代表结果比瞎蒙还差(当然也没有什么实际意义,实际上出现得很少);正值越接近1代表一致性越好。通常0.75以上表示一致性较满意,0.4以下一致性不好。但是对于测量系统来说,需要在0.9以上才能说是好的测量系统。
例2:某工厂针对注塑产品表面质量一般采用人工和设备两种方式进行检验。为了了解两种检验方式的一致性,随机选择35件样品,采用两种方式分别进行检验,结果如下表。
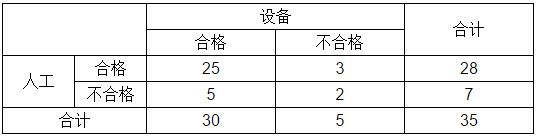
根据上面的公式计算出Kappa值为0.2,说明两种检验的结果一致性很差。
可能有人会问,这个分析并没有告诉我们哪一种更好。为了确认哪一种方法更好,可以加入标准这个因素,即由专家对样品进行仔细鉴别,确定标准的结果,然后再将两种检验方法的结果分别与此对比。其中的一张表是这样的:
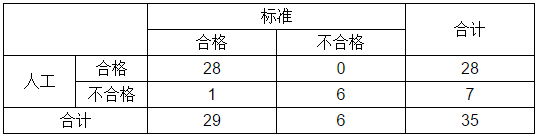
根据此表计算出的Kappa值是0.906,说明人工检验的准确率是很高的。
Kappa值很少做显著性检验,因此本文也不考虑提及其分布和检验的问题。
Kappa值也可以分析多于四格表的列联表,其P0就是自左上至右下的对角线上的格子中频数之和除以总样本量;Pe是此对角线上格子对应的行和乘以列和,然后相加再除以总样本量的平方。这样说有点难懂,我不希望再列太多的公式,用一个例子来说明一下。
例3:某个考试共有80道单选题,每题的有A、B、C、D四个答案,为考察某个考生的成绩是不是随便猜的,可以用Kappa分析做一个较确切的判断。数据表如下:
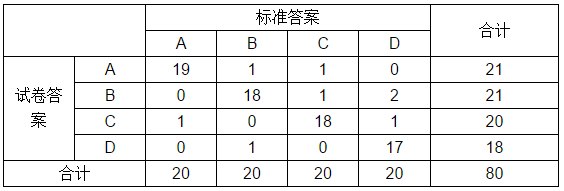
完全一致的有19+18+18+17=72,计算得P0=72/80=0.9。
Pe=(21×20+21×20+20×20+18×20)/80^2=0.25。
由此计算出Kappa=(0.9-0.25)/(1-0.25)=0.867。这个值比较大,说明学生的答案不是瞎蒙的,是真的学会了。