《剑指Offer》Java版上篇(面试题1-22,多种解题思路)
《剑指Offer》前22道题的Java版多个解题思路和代码示例。Github的地址为:https://github.com/hzka/Sword2OfferJava
面试题3:查找数组中重复的数字
问题描述:
在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2。
解题思路:
(1)较优:使用HashSet来解决。一次循环,使用contains来判断有没有重复元素,若有进行赋值并返回true,否则false。注意必须要import包。Mine
public boolean duplicate(int numbers[],int length,int [] duplication) {
HashSet hashset = new HashSet<>();
for(int i= 0;i 运行时间:20ms;占用空间:9580k
(2)先排序后(Arrays.sort(),快速排序算法)查找相邻元素。如果相邻元素相同,则返回true,否则false。注意:假设数组只有零个或者一个元素,那么返回flase,无需进行排序和后面的操作。Mine
public boolean duplicate(int numbers[],int length,int [] duplication) {
if(length == 0 || length == 1)
return false;
Arrays.sort(numbers);
for(int i = 0;i < length-1;i++){
if(numbers[i] == numbers[i+1]){
duplication[0] = numbers[i];
return true;
}
}
return false;
} 时间:38ms,空间:9420k
(3)充分利用已知条件,boolean只占一位,所以还是比较省的。
public boolean duplicate(int numbers[], int length, int[] duplication) {
boolean[] k = new boolean[length];
for (int i = 0; i < k.length; i++) {
if (k[numbers[i]] == true) {
duplication[0] = numbers[i];
return true;
}
k[numbers[i]] = true;
}
return false;
} 时间:31ms,内存:9700k
知识点:
HashTable、HashSet、HashMap的区别。
参考链接:https://blog.csdn.net/u011109589/article/details/80535412
(1)HashTable与HashMap
HashTable线程安全,添加synchronized关键字确保同步,后者不安全;前者不可使用null作为key,后者可以;初始容量不同,前者容量16,后者11;计算hash方式不同。一般使用HashMap。
(2)HashMap与HashSet
除开HashMap和Hashtable外,还有一个hash集合HashSet,有所区别的是HashSet不是key value结构,仅仅是存储不重复的元素,相当于简化版的HashMap,只是包含HashMap中的key而已。通过查看源码也证实了这一点,HashSet内部就是使用HashMap实现,只不过HashSet里面的HashMap所有的value都是同一个Object而已,因此HashSet也是非线程安全的。
面试题4:二维数组中的查找
问题描述:在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
解题思路:
(1)自己考虑的比较简单,利用二维数组由上到下,由左到右递增的规律,若target元素小于array[i][0],则元素肯定在i行之前,设置标志位flag,记录i行,然后在前i-1行利用暴力搜索的方法,若找到有,否则没有。注意:需要考虑到array长度为0或array[0]的长度为零的情况。Mine
public static boolean Find(int target, int[][] array) {
if (array.length == 0 || array[0].length == 0) return false;
int flag = array.length;
for (int i = 0; i < array.length; i++) {
if (target == array[i][0]) {
return true;
} else if (target < array[i][0]) {
flag = i;
break;
}
}
for (int i = 0; i < flag; i++) {
for (int j = 0; j < array[0].length; j++) {
if (target == array[i][j]) {
return true;
}
}
}
return false;
} 时间:173ms,空间:17468k
(2)把每一行看成有序递增的数组,利用二分查找,通过遍历每一行得到答案,时间复杂度是nlogn。
public static boolean Find(int target, int[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[0].length; j++) {
int low = 0;
int high = array[0].length - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (target < array[i][mid]) {
high = mid - 1;
} else if (target > array[i][mid]) {
low = mid + 1;
} else {
return true;
}
}
}
}
return false;
} 时间:186ms;占用内存:17516k
(3)较优:利用二维数组由上到下,由左到右递增的规律,那么选取右上角或者左下角的元素a[row][col]与target进行比较,当target小于元素a[row][col]时,那么target必定在元素a所在行的左边,即col--;当target大于元素a[row][col]时,那么target必定在元素a所在列的下边,即row++;
public static boolean Find(int target, int[][] array) {
int row=0;
int col=array[0].length-1;
while(row<=array.length-1&&col>=0){
if(target==array[row][col])
return true;
else if(target>array[row][col])
row++;
else
col--;
}
return false;
}时间:198ms,空间:17308k。
面试题5:替换空格
问题描述:请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
解题思路:
(1)较优:查找元素为空格的地方,将其用replace方法进行替换,然后不遍历这些,使用i=i+2。最后toString方法。注意:牛客网没有代码调试和代码补全功能,需要记住有些API,譬如:stringbuffer.length;str.charat(i);str.replace(begin,end,”%20”);等。Mine
public static String replaceSpace(StringBuffer str) {
for(int i = 0;i 运行时间:26ms;占用内存:9376k
(2)不考虑java里现有的replace方法。从前往后替换,后面的字符要不断往后移动,要多次移动,所以效率低下。从后往前,先计算需要多少空间,然后从后往前移动,则每个字符只为移动一次,这样效率更高一点。
public static String replaceSpace(StringBuffer str) {
int spacenum = 0;//spacenum为计算空格数
for(int i=0;i=0 && indexold 运行时间:20ms;占用内存:9524k
(3)一行搞定:
return str.toString().replaceAll(" " , "%20"); 运行时间:15ms,占用内存:9668k
知识点:
String、StringBuffer和StringBuilder的相似点与不同点:
参考链接:https://www.cnblogs.com/su-feng/p/6659064.html
1.运行速度,或者说是执行速度,在这方面运行速度快慢为:StringBuilder > StringBuffer > String;String为字符串常量,而StringBuilder和StringBuffer均为字符串变量,即String对象一旦创建之后该对象是不可更改的,但后两者的对象是变量,是可以更改的。
2.线程安全;在线程安全上,StringBuilder是线程不安全的,而StringBuffer是线程安全的;如果一个StringBuffer对象在字符串缓冲区被多个线程使用时,StringBuffer中很多方法可以带有synchronized关键字,所以可以保证线程是安全的,但StringBuilder的方法则没有该关键字,所以不能保证线程安全,有可能会出现一些错误的操作。
3.String:适用于少量的字符串操作的情况;StringBuilder:适用于单线程下在字符缓冲区进行大量操作的情况;StringBuffer:适用多线程下在字符缓冲区进行大量操作的情况
面试题6:从尾到头打印链表
题目描述:
输入一个链表,按链表值从尾到头的顺序返回一个ArrayList。
解题思路:
(1)先将链表中的每一个元素遍历拿到,将其存储至Arraylist数组中。然后再实现就地逆置。小于一半长度的元素就可以了,不用小于等于。注意:1.Arraylist存储时的判定条件2.逆置时的条件3.Arraylist使用set和get方法来存储和读取元素。Mine
public ArrayList printListFromTailToHead(ListNode listNode) {
ArrayList returnlist = new ArrayList();
if(listNode==null) return returnlist;
for (; listNode != null; listNode = listNode.next) {
returnlist.add(listNode.val);
}
for(int i = 0;i 运行时间:21ms;占用内存:9312k
(2)借助递归实现(递归的本质还是使用了堆栈结构)
ArrayList returnlist = new ArrayList();
public ArrayList printListFromTailToHead(ListNode listNode) {
if (listNode != null) {
printListFromTailToHead(listNode.next);
returnlist.add(listNode.val);
}
return returnlist;
} 运行时间:20ms;占用内存:9260k
(3)较优:借用堆栈的先进后出
public ArrayList printListFromTailToHead(ListNode listNode) {
//借用堆栈的先进后出
ArrayList returnlist = new ArrayList();
Stack stack = new Stack();
while (listNode!=null){
//堆栈压栈
stack.push(listNode.val);
//更新当前节点
listNode = listNode.next;
}
while (!stack.isEmpty()){
returnlist.add(stack.pop());
}
return returnlist;
} 运行时间:15ms;占用内存:9164k
**(第一遍不会)
面试题7:重建二叉树
问题描述:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
解决思路:肯定用递归,没话说。手动可以构建二叉树,但写的话思路不多,主要在对于递归不熟,重点在计算遍历左右子树的两个数组的开始位置和结束位置,记得进行输入合法性判断和判断溢出条件。
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
/**
* 输入合法性判断
*/
if (pre == null || in == null || pre.length != in.length) {
return null;
}
return construct(pre, 0, pre.length - 1, in, 0, in.length - 1);
}
private TreeNode construct(int[] pre, int pre_start, int pre_end, int[] in, int in_start, int in_end) {
if (pre_start > pre_end) return null;
//取前序遍历的第一个数字为根节点
int value = pre[pre_start];
//在中序中遍历寻找该根节点
int index = in_start;
while (index <= in_end && value != in[index]) {
index++;
}
//判断溢出条件
if (index > in_end) throw new RuntimeException("Invalid Input");
//创建当前根节点,并为节点赋值
TreeNode treeNode = new TreeNode(value);
//递归调用构建当前节点的左子树
treeNode.left = construct(pre, pre_start + 1, pre_start + index - in_start, in, in_start, index - 1);
//先序遍历而言,左子树开始位置是pre_start+1,结束位置是pre_start+index-in_start;
//中序遍历而言,左子树开始位置是in_start,结束位置是middle -1;
//递归调用当前节点的右子树
treeNode.right = construct(pre, pre_start + index - in_start + 1, pre_end, in, index + 1, in_end);
return treeNode;
}
}知识点:
递归:https://mp.weixin.qq.com/s/kFaJ_aYV7o-_8Ql3w4o1GA https://mp.weixin.qq.com/s/dSZH2VT8i8rVqUEPpyrHwQ
从未知到已知,再从已知到为止。1.一个问题的解可以分解为几个子问题的解;2. 这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样;3. 存在递归终止条件,即存在递归出口。
**(第一遍卡了蛮久,也没做出来,其实真的就差后面的一步)
面试题8:二叉树的下一个结点
问题描述:给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
算法思路:
1、如果该结点有右子树,则该结点的下一个结点为该结点的右子树的最左结点。
2、如果该结点没有右子树,则又分两种情况讨论:
情况一:如果该结点为该结点的父结点的左孩子,则该结点的父结点pNode.next则为下一个结点。
情况二:如果该结点为该结点的父结点的右孩子,则该结点的父结点的父结点的父结点,直到其中的一个父结点是这个父结点的左孩子,则该父结点的父结点为下一个结点。
代码示例:
public TreeLinkNode GetNext(TreeLinkNode pNode)
{
if(pNode == null) return null;
//1.如果有右子树,那么下一个结点就是右子树最左边的节点。
if(pNode.right!=null){
pNode = pNode.right;
while (pNode.left != null) pNode = pNode.left;
return pNode;
}
//2.如果没有右子树,分两种情况,(1)如果该结点的为父结点的左孩子,则该结点的父节点pNode.next则为该结点的下一个结点。
//(2)如果该结点的为父节点的右孩子,则向上找父节点,直到父节点为该父节点的左孩子,则该父节点的父节点为下一个结点。
while(pNode.next!=null){
if(pNode.next.left == pNode) return pNode.next;
pNode = pNode.next;
}
//3.如果遍历到根节点,说明是从右边上来的,返回null。
return null;
} 运行时间:21ms,占用内存:9820k
*(第一遍时有一个点没想到,如何利用第二个堆栈达到pop的效果没想明白;但第二点不停更新第一个堆栈的值想到了)
面试题9:用两个栈实现队列
题目描述:
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
解决思路:首先队列先进先出,尾部插入,头部删除。堆栈后进先出。思路如下:1.将队列中的元素“abcd”压入stack1中,此时stack2为空;2.将stack1中的元素逐个pop并Push进stack2中,此时pop一下stack2中的元素,就可以达到和队列删除数据一样的顺序了;3.如果此时整体有元素入队列,参考步骤2,先将stack2的元素整体pop并push进stack1;再将新元素插入,达到一致的顺序。(这个问题其实不难,为什么第一次没想到)
代码示例:
import java.util.ArrayList;
import java.util.Stack;
public class Solution{
Stack stack1 = new Stack();
Stack stack2 = new Stack();
public void push(int node) {
while (!stack2.isEmpty()){
stack1.push(stack2.pop());
}
stack1.push(node);
}
public int pop() {
while (!stack1.isEmpty()){
stack2.push(stack1.pop());
}
return stack2.pop();
}
} 运行时间:14ms;占用内存:9188k。
面试题10:斐波那契数列
题目描述:
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。n<=39
解决思路:
第一种:递归法:在数学上,斐波纳契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)O(2^n)Mine
第二种:(较优)直接求解法(动态编程计算斐波那契数列): 新的时间复杂度为O(n)。动态编程通过解决子问题,将子问题的结果结合来获得整个问题的解得过程。递归效率不高,子问题重叠。动态编程的思想是只解决子问题一次,将子问题解决存储以备后用。Mine
代码示例:
public static int Fibonacci01(int n) {
if(n==1) return 1;
if(n==0) return 0;
return Fibonacci01(n-1)+Fibonacci01(n-2);
}
运行时间:1215ms;占用内存:9428k
public static int Fibonacci(int n) {
if(n==1) return 1;
if(n==0) return 0;
int f_n2 = 0,f_n1 = 1;
for(int i = 1;i运行时间:18ms;占用内存:9164k
面试题11:旋转数组的最小数字
题目描述:
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转,输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。 NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
解题思路:
第一种:顺序遍历,O(n)复杂度,找到最小元素;或者Arrays.sort进行快速排序,然后return第一个元素。Mine
第二种:剑指offer上的:
Step1.和二分查找法一样,我们用两个指针分别指向数组的第一个元素和最后一个元素。
Step2.接着我们可以找到数组中间的元素:
如果该中间元素位于前面的递增子数组,那么它应该大于或者等于第一个指针指向的元素。此时数组中最小的元素应该位于该中间元素的后面。我们可以把第一个指针指向该中间元素,这样可以缩小寻找的范围。移动之后的第一个指针仍然位于前面的递增子数组之中。如果中间元素位于后面的递增子数组,那么它应该小于或者等于第二个指针指向的元素。此时该数组中最小的元素应该位于该中间元素的前面。
Step3.接下来我们再用更新之后的两个指针,重复做新一轮的查找。
代码示例:
public static int minNumberInRotateArray(int[] array) {
int min = Integer.MAX_VALUE;
for (int i = 0; i < array.length; i++) {
if (array[i] < min) {
min = array[i];
}
}
return min;
}运行时间:333ms;占用内存:27944k
public static int minNumberInRotateArray(int[] array) {
if (array.length == 0) return Integer.MIN_VALUE;
int index_first = 0, index_last = array.length - 1, index_mid = 0;
while (array[index_first] >= array[index_last]) {
if (index_last - index_first == 1) {
index_mid = index_last;
break;
}
index_mid = (index_first + index_last) / 2;
if (array[index_first] == array[index_mid] && array[index_mid] == array[index_last]) {
return GetMinInorder(array, index_first, index_last);
}
if (array[index_mid] >= array[index_first]) {
index_first = index_mid;
} else if (array[index_mid] <= array[index_first]) {
index_last = index_mid;
}
}
return array[index_mid];
}
private static int GetMinInorder(int[] array, int index_first, int index_last) {
int result = array[index_first];
for(int i = index_first+1;i<=index_last;i++){
if(result>array[i]){
result = array[i];
}
}
return result;
}运行时间:244ms;占用内存:28460k
(**)面试题12:矩阵中的路径
题目描述
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则之后不能再次进入这个格子。 例如 a b c e s f c s a d e e 这样的3 X 4 矩阵中包含一条字符串"bcced"的路径,但是矩阵中不包含"abcb"路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入该格子。
算法思路:(道理我都懂,可就是写不出来,气死了)
(1)根据给定数组,初始化一个标志位数组,初始化为false,表示未走过,true表示已经走过,不能走第二次
(2)根据行数和列数,遍历数组,先找到一个与str字符串的第一个元素相匹配的矩阵元素,进入judge
(3)根据i和j先确定一维数组的位置,因为给定的matrix是一个一维数组
(4)确定递归终止条件:越界,当前找到的矩阵值不等于数组对应位置的值,已经走过的,这三类情况,都直接false,说明这条路不通
(5)若k,就是待判定的字符串str的索引已经判断到了最后一位,此时说明是匹配成功的
(6)下面就是本题的精髓,递归不断地寻找周围四个格子是否符合条件,只要有一个格子符合条件,就继续再找这个符合条件的格子的四周是否存在符合条件的格子,直到k到达末尾或者不满足递归条件就停止。
(7)走到这一步,说明本次是不成功的,我们要还原一下标志位数组index处的标志位,进入下一轮的判断。
代码示例:
public static boolean hasPath(char[] matrix, int rows, int cols, char[] str) {
boolean[] flag = new boolean[matrix.length];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if (judge(matrix, i, j, rows, cols, str, flag, 0)) {
return true;
}
}
}
return false;
}
//字符串索引初始为0即先判断字符串的第一位
private static boolean judge(char[] matrix, int i, int j, int rows, int cols, char[] str, boolean[] flag, int k) {
//转换一维数组位置
int index = i * cols + j;
//递归的终止条件
if (i < 0 || j < 0 || j >= cols || i >= rows || matrix[index] != str[k] || flag[index] == true) {
return false;
}
//若k已经到str末尾了,说明之前匹配都成功了,直接返回ture就可以了。
if (k == str.length - 1) return true;
flag[index] = true;
//回溯,递归寻找,每次找到了就给k加一,找不到,还原
if (judge(matrix, i - 1, j, rows, cols, str, flag, k + 1) ||
judge(matrix, i + 1, j, rows, cols, str, flag, k + 1) ||
judge(matrix, i, j - 1, rows, cols, str, flag, k + 1) ||
judge(matrix, i, j + 1, rows, cols, str, flag, k + 1)) {
return true;
}
//走到这,说明走不通,还原,再试试其他路径
flag[index] = false;
return false;
} 运行时间:26ms;占用内存:9440k
知识点:
回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
回溯法对任一解的生成,一般都采用逐步扩大解的方式。每前进一步,都试图在当前部分解的基础上扩大该部分解。它在问题的状态空间树中,从开始结点(根结点)出发,以深度优先搜索整个状态空间。这个开始结点成为活结点,同时也成为当前的扩展结点。在当前扩展结点处,搜索向纵深方向移至一个新结点。这个新结点成为新的活结点,并成为当前扩展结点。如果在当前扩展结点处不能再向纵深方向移动,则当前扩展结点就成为死结点。此时,应往回移动(回溯)至最近的活结点处,并使这个活结点成为当前扩展结点。回溯法以这种工作方式递归地在状态空间中搜索,直到找到所要求的解或解空间中已无活结点为止。
(*)面试题13:机器人的运动范围
题目描述
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。但是,它不能进入方格(35,38),因为3+5+3+8 = 19。请问该机器人能够达到多少个格子?
算法思路一:(思路清楚,可是写出来竟然花费了一个半小时,而且代码真的写的很烂)
1.建立标志数组,用来记录是否遍历过。
2.判断各种越界情况(判断该点是都在矩阵中)。
3.计算位置并判断该位置是否满足要求,计数器加一并将该位置的flags标志位置为true。
4.四向遍历,不往回回溯,譬如往右走一个单位,考虑该节点是否遍历过,该节点是否在矩阵中,该节点的越界情况,该节点是否之前遍历过。Mine
代码示例:
public class Main {
private static int counting = 0;
public static void main(String[] args) {
System.out.println(movingCount(10, 1, 100));
}
public static int movingCount(int threshold, int rows, int cols) {
//第一个参数是数组是数字k,第二个是行,第三个是列。
boolean[] flags = new boolean[rows * cols];
howmanyblocks(threshold, rows, cols, 0, 0, flags);
return counting;
}
private static boolean howmanyblocks(int threshold, int rows, int cols, int i, int j, boolean[] flags) {
int index = i * cols + j;
//第一种判断各种越界情况
if (i < 0 || j < 0 || i >= rows || j >= cols) {
return false;
}
//第二种判断该位置是否满足要求
if (judgetruorfalse(i, j, threshold)) {
return false;
}
counting++;
flags[index] = true;
if (!judgetruorfalse(i - 1, j, threshold) && (((i - 1) * cols + j) >= 0) && (((i - 1) * cols + j) < rows * cols) && !flags[(i - 1) * cols + j]
) {
howmanyblocks(threshold, rows, cols, i - 1, j, flags);
}
if (!judgetruorfalse(i + 1, j, threshold) && ((i + 1) * cols + j) >= 0 && ((i + 1) * cols + j) < rows * cols && !flags[(i + 1) * cols + j]
) {
howmanyblocks(threshold, rows, cols, i + 1, j, flags);
}
if (!judgetruorfalse(i, j - 1, threshold) && (i * cols + j - 1) >= 0 && (i * cols + j - 1) < rows * cols && !flags[i * cols + j - 1]
) {
howmanyblocks(threshold, rows, cols, i, j - 1, flags);
}
if (!judgetruorfalse(i, j + 1, threshold) && (i * cols + j + 1) >= 0 && (i * cols + j + 1) < rows * cols && !flags[i * cols + j + 1]
) {
howmanyblocks(threshold, rows, cols, i, j + 1, flags);
}
return true;
}
private static boolean judgetruorfalse(int i, int j, int threshold) {
int rows_Num = String.valueOf(i).length();
int cols_Num = String.valueOf(j).length();
int add_result = 0;
for (int k = 0; k < rows_Num; k++) {
add_result += (String.valueOf(i).charAt(k) - '0');
}
for (int k = 0; k < cols_Num; k++) {
add_result += (String.valueOf(j).charAt(k) - '0');
}
if (add_result > threshold) return true;
else return false;
}
}算法思路二:
1.从(0,0)开始走,每成功走一步标记当前位置为true,然后从当前位置往四个方向探索,返回1 + 4 个方向的探索值之和。
2.探索时,判断当前节点是否可达的标准为:
1)当前节点在矩阵内;
2)当前节点未被访问过;
3)当前节点满足limit限制。
代码示例:
public int movingCount(int threshold, int rows, int cols) {
boolean[][] visited = new boolean[rows][cols];
return countingSteps(threshold, rows, cols, 0, 0, visited);
}
private int countingSteps(int threshold, int rows, int cols, int i, int j, boolean[][] visited) {
if (i < 0 || i >= rows || j < 0 || j >= cols || visited[i][j] || (bitSum(i) + bitSum(j) > threshold))
return 0;
visited[i][j] = true;
return countingSteps(threshold, rows, cols, i - 1, j, visited) +
countingSteps(threshold, rows, cols, i + 1, j, visited) +
countingSteps(threshold, rows, cols, i, j - 1, visited) +
countingSteps(threshold, rows, cols, i, j + 1, visited) + 1;
}
private static int bitSum(int i) {
int count = 0;
while (i != 0) {
count += i % 10;
i /= 10;
}
return count;
}运行时间:14ms;占用内存:9560k
面试题15:二进制中1的个数
题目描述:
输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
算法思路一:
1.对于正整数,除以2,看余数是否等于1,若是,计数器加一。2.对于负整数,使用Integer.toBinaryString(n)这一API投机取巧将其转为补码形式的字符串。然后再行计算等于1的情况。Mine
代码示例一:
public int NumberOf1(int n){
int count = 0;
if (n > 0) {
while (n / 2 != 0) {
if (n % 2 == 1) count++;
n = n / 2;
}
if (n % 2 == 1) count++;
} else {
String s1 = Integer.toBinaryString(n);
for (int i = 0; i < s1.length(); i++) {
if (s1.charAt(i) == '1') count++;
}
}
return count;
} 运行时间:13ms;占用内存:9372k
算法思路二:(较优)由于除法的效率要比移位运算要差很多,1的二进制是 前面都是0,最后一位为1,也就是只有一个1,每次向左移位一下,使得flag的二进制表示中始终只有一个位为1,每次与n做位与操作,这样就相当于逐个检测n的每一位是否是1了。
代码示例二:
public static int NumberOf1(int n) {
int count = 0;
int flag = 1;
while (flag != 0) {
if((flag & n)!=0) count++;
flag = flag << 1;
}
return count;
} 运行时间:14ms;占用内存:9228k
算法思路三:记住结论即可:把一个整数减去1,再和原整数做与运算,会把该整数最右边的1变为0,那么一个整数中二进制表示有多少个1,就会进行多少次这样的操作。
代码示例三:
public static int NumberOf1(int n) {
int count = 0;
while (n != 0) {
count++;
n = (n-1)&n;
}
return count;
}运行时间:13ms;占用内存:9376k
面试题16:数值的整数次方
题目描述:
给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。
算法思路一:
使用Math.pow这一API直接计算;(较优)或者考虑指数为正负的情况,实现类乘操作。
代码示例一:
public static double Power(double base, int exponent) {
return Math.pow(base, exponent);
}
运行时间:63ms;占用内存:10384k
public static double Power(double base, int exponent) {
double result = 1.0;
if (exponent == 0) return 1;
for (int i = 0; i < Math.abs(exponent); i++) {
result *= base;
}
if (exponent > 0) {
return result;
} else {
return 1.0 / result;
}
} 运行时间:39ms;占用内存:10544k
算法思路二:
1.全面考察指数的正负、底数是否为零等情况。
2.写出指数的二进制表达,例如13表达为二进制1101。
3.举例:10^1101 = 10^0001*10^0100*10^1000。
4.通过&1和>>1来逐位读取1101,为1时将该位代表的乘数累乘到最终结果。
代码示例:
public static double Power(double base, int n) {
double res = 1,curr = base;
int exponent;
if(n>0){
exponent = n;
}else if(n<0){
if(base==0)
throw new RuntimeException("分母不能为0");
exponent = -n;
}else{// n==0
return 1;// 0的0次方
}
while(exponent!=0){
if((exponent&1)==1)
res*=curr;
curr*=curr;// 翻倍
exponent>>=1;// 右移一位
}
return n>=0?res:(1/res);
}运行时间:69ms;占用内存:10396k
(*)面试题18:删除链表中重复的结点
题目描述:
在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。 例如,链表1->2->3->3->4->4->5 处理后为 1->2->5
算法思路:
1.假设该链表只有一个或零个节点,返回pHead即可;
2.若当前节点不重复,则保留当前结点,从下一个结点开始递归;
3.若当前节点重复,则跳过值与当前结点相同的全部结点,找到第一个与当前结点不同的结点, 从第一个与当前结点不同的结点开始递归。(注意下意识跳过第一个,自己是没有跳,所以报错。后面一直与第一个相对比)
代码示例:
public ListNode deleteDuplication(ListNode pHead)
{
//新建一个头结点
ListNode first = new ListNode(-1);
//这个头结点的下一个结点为pHead
first.next = pHead;
//p结点为pHead
ListNode p = pHead;
//last结点为新建的头结点
ListNode last = first;
while (p != null && p.next != null) {
if (p.val == p.next.val) {
int val = p.val;
while (p!= null&&p.val == val)
p = p.next;
last.next = p;
} else {
last = p;
p = p.next;
}
}
return first.next;
} 运行时间:34ms;占用内存:9532k。
(**)面试题19:正则表达式匹配
题目描述
请实现一个函数用来匹配包括'.'和'*'的正则表达式。模式中的字符'.'表示任意一个字符,而'*'表示它前面的字符可以出现任意次(包含0次)。 在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串"aaa"与模式"a.a"和"ab*ac*a"匹配,但是与"aa.a"和"ab*a"均不匹配。
代码思路一:
直接调用API即可。
代码示例一:
public static boolean match(char[] str, char[] pattern) {
String strs = String.valueOf(str);
String patterns = String.valueOf(pattern);
return strs.matches(patterns);
}代码思路二:
当模式中的第二个字符不是“*”时:
1、如果字符串第一个字符和模式中的第一个字符相匹配,那么字符串和模式都后移一个字符,然后匹配剩余的。
2、如果 字符串第一个字符和模式中的第一个字符相不匹配,直接返回false。
而当模式中的第二个字符是“*”时:
如果字符串第一个字符跟模式第一个字符不匹配,则模式后移2个字符,继续匹配。如果字符串第一个字符跟模式第一个字符匹配,可以有3种匹配方式:
1、模式后移2字符,相当于x*被忽略;
2、字符串后移1字符,模式后移2字符;
3、字符串后移1字符,模式不变,即继续匹配字符下一位,因为*可以匹配多位;
代码示例二:
public static boolean match(char[] str, char[] pattern) {
if (str == null || pattern == null) {
return false;
}
int strIndex = 0;
int patternIndex = 0;
return matchCore(str, strIndex, pattern, patternIndex);
}
private static boolean matchCore(char[] str, int strIndex, char[] pattern, int patternIndex) {
//有效性检查,str到尾,patter到尾,此时匹配成功。
if (strIndex == str.length && patternIndex == pattern.length) return true;
//pattern先到尾,匹配失败
if (strIndex != str.length && patternIndex == pattern.length) return false;
//模式第2个是*,且字符串第1个跟模式第1个匹配,分3种匹配模式;如不匹配,模式后移2位
if (patternIndex + 1 < pattern.length && pattern[patternIndex + 1] == '*') {
if (strIndex != str.length && pattern[patternIndex] == str[strIndex] || (pattern[patternIndex] == '.' && strIndex != str.length)) {
return matchCore(str, strIndex, pattern, patternIndex + 2) ||//模式后移2,视为x*匹配0个字符
matchCore(str, strIndex + 1, pattern, patternIndex + 2) ||//视为模式匹配1个字符
matchCore(str, strIndex + 1, pattern, patternIndex);//*匹配1个,再匹配str中的下一个
} else {
return matchCore(str, strIndex, pattern, patternIndex + 2);
}
}
//模式第2个不是*,且字符串第1个跟模式第1个匹配,则都后移1位,否则直接返回false
if((strIndex!=str.length && pattern[patternIndex]==str[strIndex])||(pattern[patternIndex]=='.' && strIndex!=str.length)){
return matchCore(str,strIndex+1,pattern,patternIndex+1);
}
return false;
}(*)面试题20:表示数值的字符串
题目描述
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串"+100","5e2","-123","3.1416"和"-1E-16"都表示数值。 但是"12e","1a3.14","1.2.3","+-5"和"12e+4.3"都不是。
算法思路一:
使用JVM的强制类型转换Double.parseDouble的API,若报错,则返回false,若成功,则返回true。(又投机取巧,服了自己了)Mine
代码示例一:
public static boolean isNumeric(char[] str) {
String s1 = String.valueOf(str);
try {
Double var = Double.parseDouble(s1);
} catch (Exception e) {
return false;
}
return true;
} 运行时间:17ms;占用内存:9412k
算法思路二:(较优,虽然可以想明白,但自己写的话还是有点凌乱)
1.对字符串中的每个字符进行判断分析
2.e(E)后面只能接数字,并且不能出现2次
3. 对于+、-号,只能出现在第一个字符或者是e的后一位
4.对于小数点,不能出现2次,e后面不能出现小数点
代码示例二:
public static boolean isNumeric(char[] str) {
//标记符号、小数点、e是否出现过。
boolean sign = false, decimal = false, hasE = false;
for (int i = 0; i < str.length; i++) {
//1.确保e后面必须有数字,2.确保不能同时存在两个e。
if (str[i] == 'e' || str[i] == 'E') {
if (i == str.length - 1) return false;
if (hasE) return false;
hasE = true;
} else if (str[i] == '+' || str[i] == '-') {
//1.第二次出现+-号,则其必须紧接在e之后。2.第一次出现+-时,且不是在字符串开头,
// 则必须接在e之后
if (sign && str[i - 1] != 'e' && str[i - 1] != 'E') return false;
if (!sign && i > 0 && str[i - 1] != 'e' && str[i - 1] != 'E') return false;
sign = true;
} else if (str[i] == '.') {
//e后面不能接小数点,小数点不能超过两次
if (hasE || decimal) return false;
decimal = true;
} else if (str[i] < '0' || str[i] > '9') {
//排除掉不合法字符
return false;
}
}
return true;
} 运行时间:14ms;占用内存:9356k
(*)面试题21:调整数组顺序使奇数位于偶数前面
题目描述
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
算法思路一:
建立一个Arraylist数组,第一遍遍历Array数组将偶数依次添加进动态数组中;第二遍遍历依次添加进动态数组中。最后将Arraylist数组挨个赋值给Array数组。因为题目对空间的限制比较宽泛,因此可以这么干。Mine
代码示例一:
public static void reOrderArray(int[] array) {
ArrayList arraylist = new ArrayList();
for (int i = 0; i < array.length; i++) {
if (array[i] % 2 != 0) {
arraylist.add(array[i]);
}
}
for (int i = 0; i < array.length; i++) {
if (array[i] % 2 == 0) {
arraylist.add(array[i]);
}
}
for(int i = 0;i 运行时间:23ms;占用内存:9280k
算法思路二:
使用Arraylist存偶数,使用交换法将所有奇数按照次序排好队(第二个指针遇到偶数往前走,直至奇数;第一个指针遇到奇数往前走,直到偶数;假如第一个指针是偶数,第二个指针是奇数且第一个指针的位置小于第二个位置。则交换位置;否则,第二个指针走得慢,让它再往前走一格。),再进行后半部分偶数的赋值Mine
代码示例二:
public static void reOrderArray(int[] array) {
ArrayList arraylist = new ArrayList();
for (int i = 0; i < array.length; i++) {
if (array[i] % 2 == 0) {
arraylist.add(array[i]);
}
}
int first_ele = 0, second_ele = 0;
while (second_ele < array.length && first_ele 运行时间:22ms;占用内存:9412k
算法思路三:(较优)为了保持相对位置的不变(稳定性),采用冒泡排序的思想,记录已经排好位置的奇数的个数,若后续存在奇数,则将其挨个冒泡交换。很巧。
代码示例三:
public static void reOrderArray(int [] array) {
//相对位置不变,稳定性
//冒泡排序的思想
int m = array.length;
int k = 0;//记录已经摆好位置的奇数的个数
for (int i = 0; i < m; i++) {
if (array[i] % 2 == 1) {
int j = i;
while (j > k) {//j >= k+1
int tmp = array[j];
array[j] = array[j-1];
array[j-1] = tmp;
j--;
}
k++;
}
}
}运行时间:15ms;占用内存:9360k
面试题22:链表中倒数第k个结点
题目描述
输入一个链表,输出该链表中倒数第k个结点。
算法思路一:遍历第一遍链表,获得链表长度,如果k大于链表长度,则返回null,否则计算真实位置(总长度-k)。然后再顺序查找到总长度-k的位置,返回该ListNode。Mine
代码示例一:
public static ListNode FindKthToTail(ListNode head,int k) {
//计算listnode的总长度
ListNode store_point = head;
int listnode_length = 0;
while(head!=null){
listnode_length++;
head = head.next;
}
if(k > listnode_length) return null;
int real_pos = listnode_length - k;
for(int i = 0;i 运行时间:22ms;占用内存:9516k
代码思路二:
两个指针,先让第一个指针和第二个指针都指向头结点,然后再让第一个指正走(k-1)步,到达第k个节点。然后两个指针同时往后移动,当第一个结点到达末尾的时候,第二个结点所在位置就是倒数第k个节点了。与此同时,防止链表越界。(相当于制造了一个K长度的尺子,把尺子从头往后移动,当尺子的右端与链表的末尾对齐的时候,尺子左端所在的结点就是倒数第k个结点)
代码示例二:
public static ListNode FindKthToTail(ListNode head, int k) {
if (head == null || k <= 0) return null;
ListNode tail = head;
for (int i = 0; i < k; i++) {
if (tail != null) {
tail = tail.next;
} else {
return null;
}
}
while (tail != null) {
head = head.next;
tail = tail.next;
}
return head;
}(**)面试题23:链表中环的入口结点
题目描述
给一个链表,若其中包含环,请找出该链表的环的入口结点,否则,输出null。
算法思路一:
自己想的很low。先将已经遍历过的节点存放在Arraylist数组中,判断当前节点的下一个节点是否在Arraylist中(使用contains的API)。若在则返回该节点,若不在,则继续遍历,知道pHead为Null,返回null。感觉代码复杂度应该在O(n^3)。
代码示例一:
public ListNode EntryNodeOfLoop(ListNode pHead) {
ArrayList arraylist = new ArrayList();
arraylist.add(pHead);
pHead = pHead.next;
while (pHead != null) {
if (arraylist.contains(pHead)) {
return pHead;
}
arraylist.add(pHead);
pHead = pHead.next;
}
return null;
} 运行时间:24ms;占用内存:9652k
算法思路二:(较优,感觉记住咋操作就行了,没必要记原因)
第一步,用两个快慢指针找环中相汇点。分别用slow, fast指向链表头部,slow每次走一步,fast每次走二步,直到fast == slow找到在环中的相汇点。
第二步,找环的入口。当fast == slow时,假设slow走过x个节点,则fast走过2x个节点。设环中有n个节点,因为fast比slow多走一圈(n个节点),所以有等式2x = n + x,可以推出n = x,两者同时减去蓝色部分,算出来相等,都为n-x。这时,我们让fast重新指向链表头部pHead,slow的位置不变,然后slow和fast一起向前每次走一步,直到fast == slow,此时两个指针相遇的节点就是环的入口。
参考链接:https://www.jianshu.com/p/092d14d13216
证明链接:https://www.nowcoder.com/questionTerminal/253d2c59ec3e4bc68da16833f79a38e4
代码示例二:
public ListNode EntryNodeOfLoop(ListNode pHead){
if(pHead==null|| pHead.next==null|| pHead.next.next==null)return null;
ListNode fast=pHead.next.next;
ListNode slow=pHead.next;
//先判断有没有环
while(fast!=slow){
if(fast.next!=null&& fast.next.next!=null){
fast=fast.next.next;
slow=slow.next;
}else{
//没有环,返回
return null;
}
}
//循环出来的话就是有环,且此时fast==slow.
fast=pHead;
while(fast!=slow){
fast=fast.next;
slow=slow.next;
}
return slow;
}运行时间:20ms;占用内存:9632k
(*)面试题24:反转链表
题目描述
输入一个链表,反转链表后,输出新链表的表头。
算法思路一:
利用栈的后进先出,遍历链表并逐个push进堆栈中,循环条件为head!=null,逐个pop构建新链表,但存在时间复杂度或者空间复杂度过高的问题。Mine
代码示例一:
public static ListNode ReverseList01(ListNode head) {
if(head==null || head.next ==null) return head;
Stack stack = new Stack();
while (head != null) {
stack.push(head);
head = head.next;
}
ListNode reverstnode = stack.pop();
ListNode returnnode = reverstnode;
System.out.println(reverstnode.val);
while (!stack.isEmpty()) {
reverstnode.next = stack.pop();
reverstnode = reverstnode.next;
System.out.println(reverstnode.val);
}
return returnnode;
} 时间还是空间超过限制。
算法思路二:
(较优)使用三个指针保存当前节点head、当前节点的下一个节点next以及当前节点的上一个节点pre,循环条件是head不等于空,(1)先使用next = head.next保存head的下一个节点的信息;(2)再使用head.next=pre实现断链和反转链表的效果。(3)pre=head,head=next;让pre,head,next依次往后移动一个节点,继续下一次指针的反转。
代码思路二:
public static ListNode ReverseList(ListNode head) {
if(head==null || head.next ==null) return head;
ListNode pre = null;
ListNode next =null;
while (head!=null){
next = head.next;//暂存下一个节点
head.next = pre;//断链并进行反转
pre = head;//将两个指针都往前移动一格
head = next;
}
return next;
} 运行时间:20ms;占用内存:9536k
(*)面试题25:合并两个排序的链表
题目描述
输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。
算法思路一:
我想的是插入,以list1为合成后的链表,进行比较插入,但由于是插入且维护的指针较多,所以时间复杂度较高,故而舍弃掉。新建一个链表,进行逐个比较,若list1小于list2,则将list1的节点插入,并将list1往前走一格,否则list2向前走一格。如果一个走完另一个没有走完,直接将没走完的放在合并后链表的后面,挺简单。Mine
代码示例一:
public static ListNode Merge(ListNode list1, ListNode list2) {
ListNode mergeResult = new ListNode(-1);
mergeResult.next = null;
ListNode head = mergeResult;
while (list1 != null && list2 != null) {
if (list1.val < list2.val) {
mergeResult.next = list1;
mergeResult = mergeResult.next;
list1 = list1.next;
} else {
mergeResult.next = list2;
mergeResult = mergeResult.next;
list2 = list2.next;
}
}
if (list1 != null) {
mergeResult.next = list1;
}
if(list2!=null){
mergeResult.next = list2;
}
return head.next;
} 运行时间:26ms;占用内存:9464k
算法思路二:
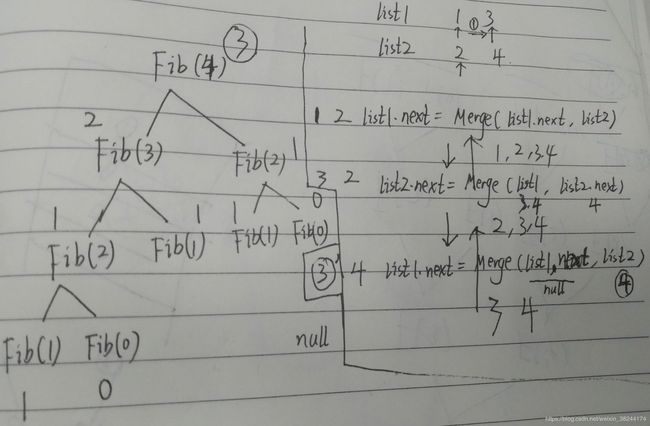
(较优)采用递归的方法进行合并。
public static ListNode Merge(ListNode list1,ListNode list2) {
if(list1 == null){
return list2;
}
if(list2 == null){
return list1;
}
if(list1.val <= list2.val){
list1.next = Merge(list1.next, list2);
return list1;
}else{
list2.next = Merge(list1, list2.next);
return list2;
}
} 运行时间:26ms;占用内存:9464k
(**)面试题26:树的子结构
题目描述
输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
算法思路一:
(1)先根遍历二叉树A,不动二叉树B;(2)假设找到A和B相等的第一个节点,递归进行判断两个二叉树的左孩子和右孩子是否都相等,递归结束条件是1.二叉树B遍历结束则返回false;2.二叉树B未遍历结束但二叉树A结束了,返回false;3.两者不相等,返回false。我自己第一步考虑到了,但第二步想的是层次遍历,未考虑递归这块,但层次遍历自己又实现不了,好吧。。
代码示例一:
public static boolean HasSubtree(TreeNode root1, TreeNode root2) {
boolean result = false;
if (root1 != null && root2 != null) {
if (root1.val == root2.val) {
result = doesTree1HaveTree2(root1, root2);
}
if (!result) result = HasSubtree(root1.left, root2);
if (!result) result = HasSubtree(root1.right, root2);
}
return result;
}
private static boolean doesTree1HaveTree2(TreeNode root1, TreeNode root2) {
if (root1 == null) return false;
if (root2 == null) return true;
if (root1.val != root2.val) return false;
return doesTree1HaveTree2(root1.left, root2.left) && doesTree1HaveTree2(root1.right, root2.right);
}运行时间:16ms占用内存:9508k