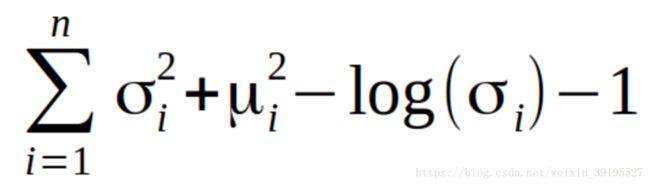大话 - 自编码(Autoencoder)和变分自编码(Variational Autoencoder)

因为最近在研究自编码和变分自编码的区别，以及应用方向，现在总结内容和大家分享一下。

自编码 (Autoencoder)

自编码（Autoencoder）在降维算法普遍被认可的一种算法，算法的主要出发点：如果有个网络，你将数据输入（N维），可以是图片或者其他特征，然后网络吐出了相同的数据，那么我们是否可以认为网络的某些隐层特点（输出, M维）可以代表你的输入数据特点？—- 因为基于这个隐层输出，网络又重新输出了原始数据。

基于这个想法，普遍的网络设置，都是将隐层设置成一个低维（M << N）, 然后将损失函数 (Loss function)设置成原始输入和输出的diff。

这里将用mnist手写数字图片数据作为一个代码样例说明, 这里我们简单将代码逻辑分几个部分进行串行讲解：

1. 网络结构
2. 前向数据流 (forward)
3. 损失函数 (loss function) & 优化器 (optimizer)
4. 训练 & 梯度下降

数据简单介绍 28 * 28维图片，图片pixel值[0, 1]，图片内容1 - 9, 知道了输入纬度，咱们直接来设置网络结构 (比如我们想将 28 * 28 降维到 64维)

网络结构

class AutoEncoder(nn.Module):
    """
    """
    def __init__(self, latent_num=16):
        """
        TODO: doconvolution
        """
        super(AutoEncoder, self).__init__()

        self.fc1 = nn.Linear(IMG_SIZE, 256)
        self.fc1.weight.data.normal_(0.0, 0.05)

        self.fc2 = nn.Linear(256, 64)
        self.fc2.weight.data.normal_(0.0, 0.05)

        self.fc3 = nn.Linear(64, 256)
        self.fc3.weight.data.normal_(0.0, 0.05)

        self.fc4 = nn.Linear(256, IMG_SIZE)
        self.fc4.weight.data.normal_(0.0, 0.05)

前向数据流 (forward)

有了网络结构，我们还需要将网络数据流串联起来，这个过程普遍成为forward,

    def forward(self, x):
        h1 = F.relu(self.fc1(x))  # IMG_SIZE -> 518
        h2 = F.relu(self.fc2(h1)) # 518 -> 256
        h3 = F.relu(self.fc3(h2)) # 256 -> 128
        h4 = F.relu(self.fc4(h3)) # 128 -> 256
        output = h4
        # output = F.sigmoid(h6)
        return output

损失函数 (Loss Function) & 优化器 (optimizer)

有了输入和输出，我们需要定量的衡量模型对数据的刻画好坏，这时候我们需要定义一个损失函数来描述模型是否能很好的刻画数据。

为了让模型能向我们想要的特性发展，我们需要一个优化器（他会根据输出和输出差了多少，对模型进行调整，并定义了调整幅度和步伐）

def loss_function(output, x):
        """
        """
        mse = encoder_loss(output, x)
        return mse

optimizer = optim.Adam(model.parameters(), lr=1e-3)

训练 & 梯度下降

接下来就是数据训练，通过观察损失函数来判断模型是否收敛

for epoch in range(num_epochs):
    train_loss = 0
    for batch_idx, data in enumerate(dataloader):
        img = data.view(data.size(0), -1)
        img = Variable(img.float())
        # free zero grad
        optimizer.zero_grad()
        output = model(img)
        # backward
        loss = loss_function(output, img)
        loss.backward()
        train_loss += loss.data[0]
        optimizer.step()
        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch,
                batch_idx * len(img),
                len(dataloader.dataset), 100. * batch_idx / len(dataloader),
                loss.data[0] / len(img)))
    print('====> Epoch: {} Average loss: {:.4f}'.format(
        epoch, train_loss / len(dataloader.dataset)))

训练后，模型输出结果:

变分自编码 (Variational Autoencoder) - 这个名字中文翻译的真是烂

这部分才是我主要想讲的，上面提到自编码，那么变分自编码是为了解决什么问题呢？ ——- 其主要思想还是希望学习隐层变量，并将其用来表示原始数据，但是它加另一个条件, 即隐层变量能学习原始数据的分布, 并反过来生产一些和原始数据相似的数据（这有啥用？—-可用于图片修复，让图片按训练集的数据分布变化）。

变分自编码 (Variational Autoencoder) 希望通过网络学习，学习隐层变量基于输入变量x的分布p(z|x) (这个貌似和标准的自编码器没啥区别？)。但是变分自编码多了一点变化，为了让隐层抓住输入数据特性, 而不是简单的输出数据=输入数据，他在隐层中假如随机噪声（单位高斯噪声）（这个过程也叫reparametrize），以确保隐层能较好抽象输入数据特点。

代码部分

网络配置

class VAE(nn.Module):
    """
    """
    def __init__(self, latent_num=2):
        """
        TODO: doconvolution
        """
        super(VAE, self).__init__()

        self.fc1 = nn.Linear(IMG_SIZE, 256)
        self.fc21 = nn.Linear(256,  16)
        self.fc22 = nn.Linear(256, 16)
        self.fc3 = nn.Linear(16, 256)
        self.fc4 = nn.Linear(256, 784)

前向数据流 (forward)

    def encoder(self, x):
        h1 = F.relu(self.fc1(x))
        mu, std = self.fc21(h1), self.fc22(h1)
        return mu, std
    def decoder(self, x):
        h2 = F.relu(self.fc3(x))
        return self.fc4(h2)

    def forward(self, x):
        mu, var = self.encoder(x)
        z = self.reparametrize(mu, var)
        return self.decoder(z), mu, var

损失函数 （Loss Function）

现在输出层和输入层存在这一定的局部差异，这是由于我们在隐层中加入了噪声带来的，但是我们如果想让隐层变量p(z|x)在不同类型输入上具有区分度，我们需要对隐层变量z做一些限制。

为了引出这个限制，我们先来看一下，我们对于这个隐层变量需要它具有哪些属性，

这里原文用 Kullback-Leibler divergence (KL divergence) 来刻画两个分布之间的差异。
原文中将隐层参量拆分成一个均值变量和一个方差变量来刻画某一纬度的输入变化, 并将均值和方差和标准高斯函数对比。 对于限定分布差异上，损失函数就是

def loss_function(output, x, mu, var):
        """
        """
        mse = encoder_loss(output, x)
        #   0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
        latent_loss = mu.pow(2).add_(var.pow(2)).mul(-1.).add_(torch.log(var.pow(2))).add_(1).mul_(0.5)
        KLD = torch.sum(latent_loss)
        return mse - KLD

训练 & 梯度下降

for epoch in range(num_epochs):
    train_loss = 0
    for batch_idx, data in enumerate(dataloader):
        img = data.view(data.size(0), -1)
        img = Variable(img.float())
        # free zero grad
        optimizer.zero_grad()
        output, mu, var = model(img)
        # backward
        loss = loss_function(output, img, mu, var)
        loss.backward()
        train_loss += loss.data[0]
        optimizer.step()
        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch,
                batch_idx * len(img),
                len(dataloader.dataset), 100. * batch_idx / len(dataloader),
                loss.data[0] / len(img)))

训练后，网络输出层图片样例：

文章中完整代码在这: https://github.com/jnuthong/pytorch_example