1.4 熄灯问题(枚举,位运算)
1222:EXTENDED LIGHTS OUT
描述
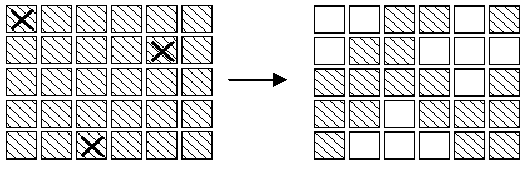
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right.
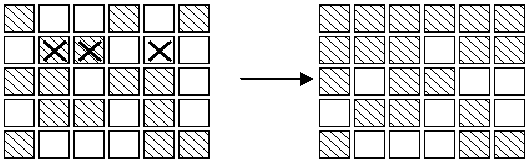
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.
Note:
1. It does not matter what order the buttons are pressed.
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once.
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.
输入
The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0抯 or 1抯 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.
输出
For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0抯 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.
样例输入
2 0 1 1 0 1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 0
样例输出
PUZZLE #1 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 PUZZLE #2 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 0 1 1 0 1
来源
Greater New York 2002
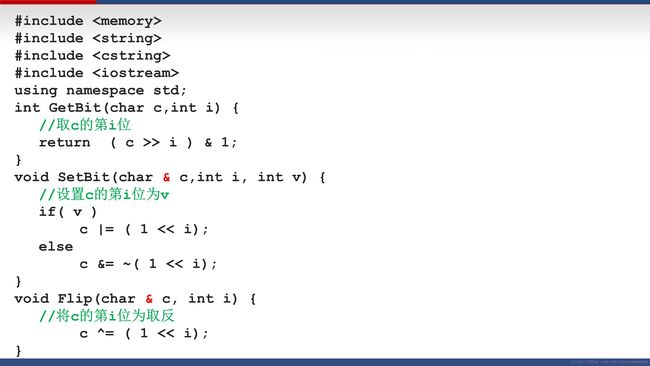
int GetBit(char c, int i) //取c的第i位
{
return (c >> i) & 1;
}一个字符占一个字节,一个字节为8个比特,即8位。即:1 Byte = 8 bit
(c >> i)&1;//从右移i位后,就将第i位移到0位处,此时与1做“&”操作,当c的第i位为1时,结果为1,当c的第i位为0时,结果为0.
void SetBit(char & c, int i, int v)//设置c的第i位为v
{
if(v)
c |= (1 << i);
else
c &= ~(1 << i);
} v可能为0也可以能为1,当v==1时,将c的第i位置为1,实现代码:
c | = (1 << i); //将1左移i位,就只有第i位为1,其他位为0,再与c做“或”操作,就将c的第i位置为1了。
1: 0000 0001 1 << 2: 0000 0100
当v== 0时,就要将i的第i位置为0,实现代码:
c &= ~(1 << i);//先将1左移i位,此时第i位为1,其余位为0,再“取反”,此时第i位为0,其他位都为1,再进行‘与’操作,此时其他位都不变,第i位变为了0.
例如:假设c为64,要将c的第6位置为0.
c: 0100 0000
第一步:1<< 6:
1: 0000 0000
1 << 6 : 0100 0000
第二步:取反
~(1<<6): 1011 1111
第三步:进行“与运算”
c &= ~(1<<6): 0000 0000 结果发现,c的其他位都不变,c的第i位置为了0.
void Flip(char &c, int i)//将c的第i位取反
{
c ^= (1 << i);
}将c的第i位0变为1,1变为0。
异或运算:相等为0,不等为1.
先将1左移i位,使得第i位为1,其余位为0,再与c做“异或运算”,此时如果c的第i位为1,则异或后第i位为0;如果c的第i位为0,则异或后,c的第i位为1。
主要就是为了将开关按下后,上下左右以及它本身灯的状态改变。
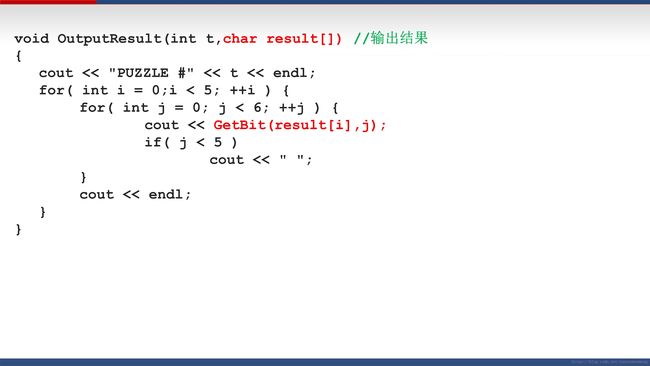
void OutputResult(int t,char result[])
{
cout << "PUZZLE #" << t << endl;
for(int i = 0; i < 5; ++i)
{
for(int j = 0; j < 6; ++j)
{
cout << GetBit(result[i],j);
if(j < 5)
{
cout << " ";
}
}
cout << endl;
}
} 输出第t组测试数据的结果。一共5行6列。GetBit(result[i],j),取第i个数的第j个比特,相当于取第i行第j列的内容。
memset(oriLights,0,sizeof(oriLights));
for(int i = 0; i < 5; ++i)
{
for(int j = 0; j < 6; ++j)
{
int s;
cin >> s;
SetBit(oriLights[i],j,s);
}
}将每一组数据输入,存放在oriLights[]数组里面。SetBit(oriLights[i], j, s);将oriLights数组第i个数的第j个比特置为s。这里orilights数组中的每一个数相当于一行,每一个数又有8个比特,本题可以用到6个比特的内容,相当于列的数据。
【注意】每一组测试数据输入之前都需要将oriLights[]数组置为0,一切都重新开始计算。
#include
#include
using namespace std;
int GetBit(char c, int i) //取c的第i位
{
return (c >> i) & 1;
}
void SetBit(char & c, int i, int v)//设置c的第i位为v
{
if(v)
c |= (1 << i);
else
c &= ~(1 << i);
}
void Flip(char &c, int i)//将c的第i位取反
{
c ^= (1 << i);
}
void OutputResult(int t,char result[])
{
cout << "PUZZLE #" << t << endl;
for(int i = 0; i < 5; ++i)
{
for(int j = 0; j < 6; ++j)
{
cout << GetBit(result[i],j);
if(j < 5)
{
cout << " ";
}
}
cout << endl;
}
}
int main()
{
char oriLights[5];//最初灯矩阵,一个比特代表一个灯
char lights[5]; //不停变化的灯矩阵
char result[5];//结果开关矩阵
char switchs;//某一行的开关状态
int T;
cin >> T;
for(int t = 1; t <= T; ++t)
{
memset(oriLights,0,sizeof(oriLights));
for(int i = 0; i < 5; ++i)
{
for(int j = 0; j < 6; ++j)
{
int s;
cin >> s;
SetBit(oriLights[i],j,s);
}
}
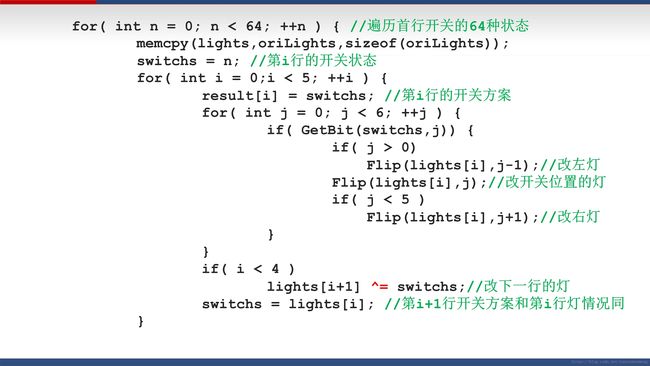
for(int n = 0; n < 64; ++n)//遍历首行开关的64种状态
{
memcpy(lights,oriLights,sizeof(oriLights));
switchs = n;//第i行的开关状态
for(int i = 0; i < 5; ++ i)
{
result[i] = switchs;
for(int j = 0; j < 6; ++j)
{
if(GetBit(switchs,j))//1的时候才翻转左右、本身、下一行的状态
{
if(j > 0)//当j左边还有值的时候
Flip(lights[i], j-1);//改左灯
Flip(lights[i],j);//改开关位置的灯
if(j < 5)//当j右边还有值的时候
{
Flip(lights[i],j+1);//改右灯
}
}
}
if(i < 4)
{
lights[i+1] ^= switchs;//改下一行的灯
}
switchs = lights[i];//第i+1行开关方案,再次执行result[i]=switchs,看下一行的状态
}
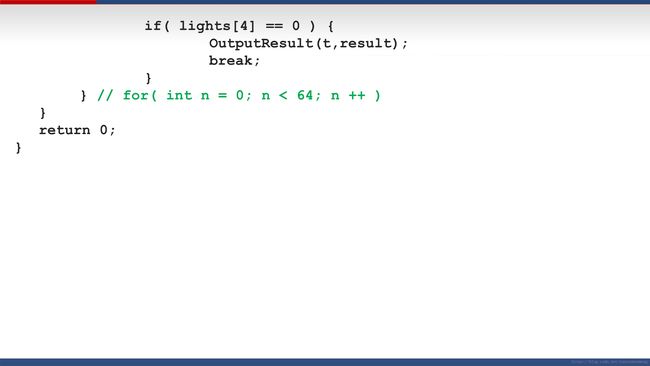
if(lights[4] == 0)
{
OutputResult(t,result);
break;
}
}
}
return 0;
}
用位运算可以使得程序的执行效率大大提升,用一个字节(8个比特)就可以搞定一行所存储所有的内容,用二进制的运算方法(位运算)进行运算,速度非常快。