（Java）leetcode-968 Binary Tree Cameras (监控二叉树)
目录
- 题目描述
- 思路：贪心
- 1. 从何选择
- 2. 着眼叶子
- 3. 贪心选择
- 3.1 dfs的返回值
- 3.2 dfs的处理
- 4. 代码
更多LeetCode题解，可移步我的解题记录，持续更新中~
题目描述
给定一个二叉树，我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1：
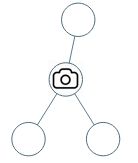
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。
示例 2：
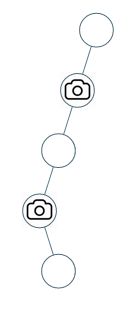
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示：
给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。
思路：贪心
1. 从何选择
该从哪下手呢？
-
考虑树中的一个节点：
它可以被其父节点、其本身，或其两个孩子覆盖。
四种选择。 -
考虑树的根：
它可以被左孩子或右孩子或其本身覆盖。
三种选择。 -
考虑树的叶子节点：
它可以被其父节点或自身覆盖。
两种选择。
如果你是选择困难症，那就从叶子节点开始入手吧，因为它需要做的选择最少。
2. 着眼叶子
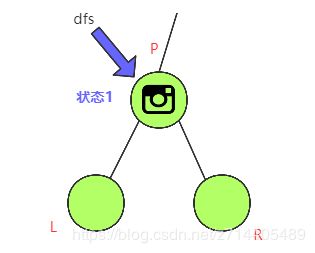
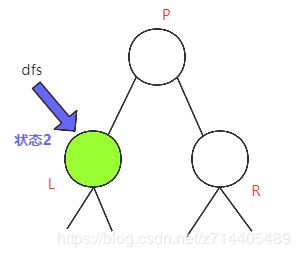
如果在叶子L处设置相机，则相机可以覆盖该叶子L及其父节点P。（见下图）
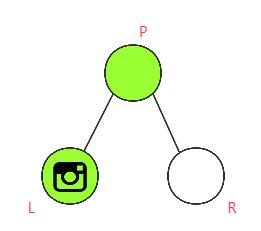
如果在它的父节点P设置相机，则该相机可以覆盖此叶子L，其父节点P及其兄弟R。（见下图）
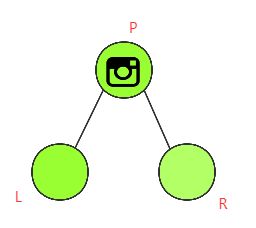
我们可以看到第二个计划总是比第一个更好，因为用同样数量的相机覆盖了更多的节点。
现在我们只有一个选择：将相机设置在所有叶子的父节点上。
3. 贪心选择
思考一个贪心的解决方案：
将相机放在所有叶子的父节点上，然后删除所有覆盖的节点。
注意这里的“删除”指的是逻辑上的，表示已经覆盖的节点我们将无视掉，不会往它们上面放摄像头。
重复步骤，直到覆盖所有节点。
说明：
提供一个递归的dfs函数，并采用后序遍历，自下而上的方式来访问节点——
3.1 dfs的返回值
先讨论dfs的返回值，每个返回值代表节点的一种状态：
如果该节点是叶子，则返回0。
如果该节点是叶子的父节点，那么它一定要装摄像头，返回1。
如果该节点已被覆盖，且该节点上没有摄像头，则返回2。
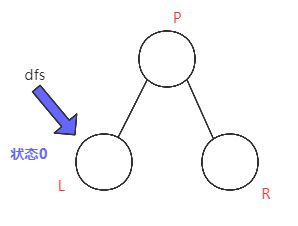
3.2 dfs的处理
由于是后序遍历，那么现在考虑获得了左孩子和右孩子状态之后需要做的处理（当前节点应该设置什么状态）。
对于每个节点，有一下三种case：
case（1）：如果它有一个孩子，且这个孩子是叶子（状态0），则它需要摄像头，res ++，然后返回1，表示已经给它装上了摄像头。
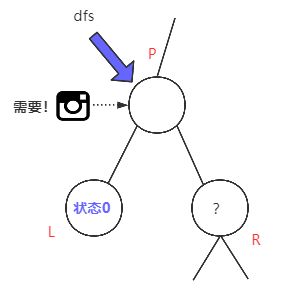
case（2）：如果它有一个孩子，且这个孩子是叶子的父节点（状态1），那么它已经被覆盖，返回2。
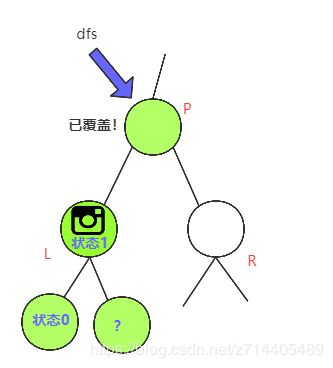
case（0）：否则，这个节点无孩子，或者说，孩子都是状态2，那么我们将这个节点视为叶子来处理。
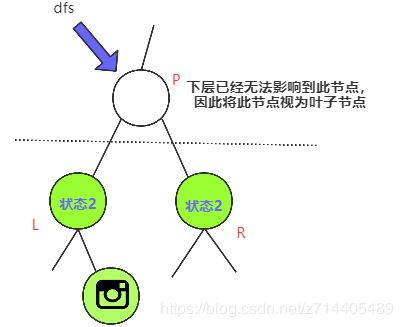
由于dfs最终返回后，整棵树的根节点的状态还未处理，因此需要判断，若根节点被视为叶子，需要在其上加一个摄像头。
4. 代码
class Solution {
int res = 0;
public int minCameraCover(TreeNode root) {
// 若根节点被视为叶子，需要在其上加一个摄像头
return (dfs(root) == 0 ? 1 : 0) + res;
}
public int dfs(TreeNode root) {
// 空节点不需要被覆盖，归入情况2
if (root == null) return 2;
// 递归求左右孩子的状态
int left = dfs(root.left);
int right = dfs(root.right);
// 获取左右孩子状态之后的处理
// 有叶子孩子，加摄像头，归入情况1
if (left == 0 || right == 0) {
res++;
return 1;
}
// 孩子上有摄像头，说明此节点已被覆盖，情况2;
if(left == 1 || right == 1) return 2;
// 否则将节点视为叶子，情况0
else return 0;
}
}
执行用时：0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗：39.4 MB, 在所有 Java 提交中击败了75.00%的用户