详解概率图模型——概述
详解概率图模型——概述
- 详解概率图模型——概述
- 概率图
- 概览
- 有向图 vs. 无向图
- 有向图
- 无向图
- 判别式(discriminative)模型 and 生成式(generative)模型
- 前言
- 两个模型的范例
- 判别式模型
- 生成式模型
- 对比
- 优缺点
详解概率图模型——概述
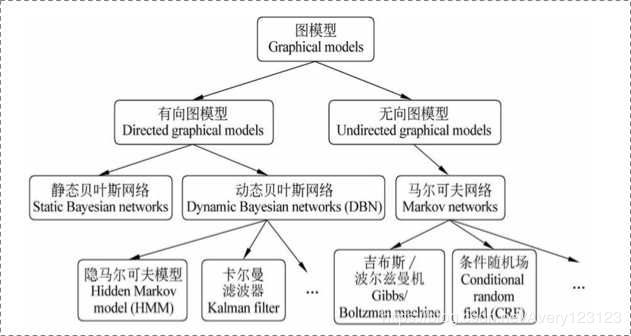
概率图
概览
有向图 vs. 无向图
有向图
举个例子,对于下面的这个有向图的随机变量
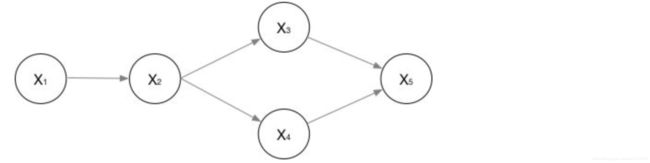
应该这样表示他们的联合概率:
![]()
贝叶斯网络:有向图模型
贝叶斯网络的一个典型案例是所谓的「学生网络(student network)」:
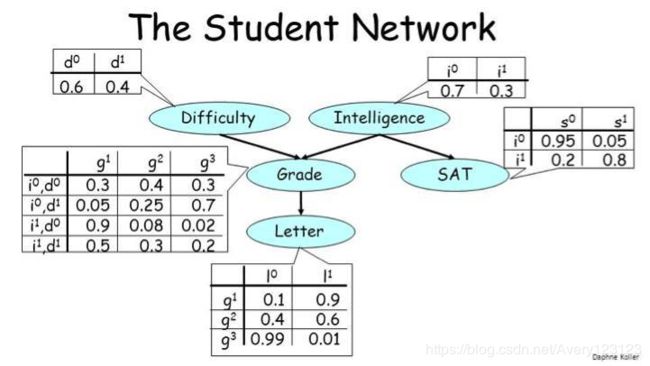
上图描述了某个学生注册某个大学课程的设定。该图中有 5 个随机变量:

该图中的边编码了这些变量之间的依赖关系。

无向图
对于无向图,我看资料一般就指马尔科夫网络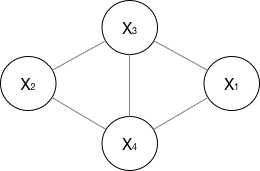
马尔可夫网络:无向图模型

为了简洁地说明,我们只探讨这个抽象的图,其中的节点 ABCDE 不像上面的例子有直接的真实案例对应。同样,这些边表示变量之间的相互作用。我们可以看到 A 和 B 彼此之间有直接的影响关系,而 A 和 C 之间则没有。
注意马尔可夫网络不需要是无环的,这一点和贝叶斯网络不一样。
判别式(discriminative)模型 and 生成式(generative)模型
前言
1、机器学习分为有监督的机器学习和无监督的机器学习;
2、有监督的机器学习就是已知训练集数据的类别情况来训练分类器(比如 分类任务),无监督的机器学习就是不知道训练集的类别情况来训练分类器(比如聚类任务);
3、有监督的机器学习中,我们可以概述为通过很多有标记的数据,训练出一个模型,然后利用这个,对输入的X进行预测输出的Y。这个模型一般有两种:
决策函数:Y=f(X)
条件概率分布:P(Y|X)
4、根据通过学习数据来获取这两种模型的方法,我们可以分为判别方法和生成方法;
判别方法:由数据直接学习决策函数Y=f(X)或条件概率分布P(Y|X)作为预测模型,即判别模型。
判别方法关心的是对于给定的输入X,应该预测什么样的输出Y。
生成方法:由数据学习联合概率分布P(X,Y), 然后由P(Y|X)=P(X,Y)/P(X)求出概率分布P(Y|X)作为预测的模型,即生成模型
生成方法表示了给定输入X与产生输出Y的生成关系
在监督学习下,模型可以分为判别式模型与生成式模型。
两个模型的范例
生成模型:朴素贝叶斯、隐马尔可夫(em算法)
判别模型:k近邻法、感知机、决策树、逻辑回归、线性回归、最大熵模型、支持向量机(SVM)、提升方法、条件随机场(CRF)
A批模型(神经网络模型、SVM、perceptron、LR、DT……)与B批模型(NB、LDA……),的区别是什么?
判别式模型
数据直接学习决策函数Y=f(X)或条件概率分布P(Y|X)得到的预测模型,就是判别模型;
生成式模型
由数据学习联合概率分布P(X,Y), 然后由P(Y|X)=P(X,Y)/P(X)求出概率分布P(Y|X)作为预测的模型,就是生成模型
对比
1、生成模型可以还原出联合概率分布(还原数据本身相似度),而判别方法不能;
2、生成方法的学习收敛速度更快,当样本容量增加的时候,学到的模型可以更快的收敛于真实模型;
3、当存在隐变量时,仍可以利用生成方法学习,此时判别方法不能用;
4、判别学习不能反映训练数据本身的特性,但它寻找不同类别之间的最优分类面,反映的是异类数据之间的差异,直接面对预测,往往学习的准确率更高,由于直接学习P(Y|X)或Y=f(X),从而可以简化学习;
5、简单的说,生成模型是从大量的数据中找规律,属于统计学习;而判别模型只关心不同类型的数据的差别,利用差别来分类。
6、 由生成模型可以得到判别模型,但由判别模型得不到生成模型。
优缺点
在监督学习中,两种方法各有优缺点,适合于不同条件的学习问题。
生成方法的特点:上面说到,生成方法学习联合概率密度分布P(X,Y),所以就可以从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度。但它不关心到底划分各类的那个分类边界在哪。生成方法可以还原出联合概率分布P(Y|X),而判别方法不能。生成方法的学习收敛速度更快,即当样本容量增加的时候,学到的模型可以更快的收敛于真实模型,当存在隐变量时,仍可以用生成方法学习。此时判别方法就不能用。
判别方法的特点:判别方法直接学习的是决策函数Y=f(X)或者条件概率分布P(Y|X)。不能反映训练数据本身的特性。但它寻找不同类别之间的最优分类面,反映的是异类数据之间的差异。直接面对预测,往往学习的准确率更高。由于直接学习P(Y|X)或P(X),可以对数据进行各种程度上的抽象、定义特征并使用特征,因此可以简化学习问题。