基于OpenCV实现二维码等图像的检测与矫正
文章目录
- 1. 效果展示
- 2. 算法流程
- 3. 算法分析(带示例)
- 1)对比度亮度调整
- 2)滤波降噪
- 3)反二值化
- 4)腐蚀膨胀处理
- 5)Canny边缘检测
- 6)Hough算子拟合直线
- 7)计算二维码四个顶点坐标
- 8)利用顶点坐标进行仿射变换
- 4. 完整代码(cpp)
- 5. 测试图片
- 6. 参考资料
1. 效果展示
首先先展示一下效果,左边是原图,右边是通过矫正后的图片。该算法适用于黑白较为分明的图像,但对于一些极端情况(比如大面积阴影,污点等等),效果不佳,因此有一定局限性。这里也仅仅提供一个算法思路,供人借鉴。

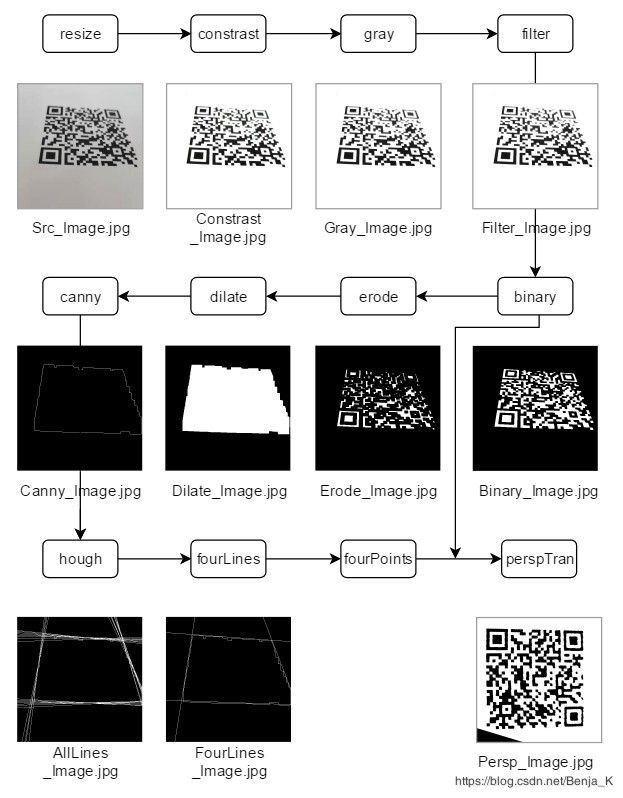
2. 算法流程
算法主要流程主要分为:
1)对比度亮度调整
通过对比度亮度调整,增加二维码和背景的分离度。
2)滤波降噪
通过滤波降噪,去除部分图像噪点。
3)反二值化
反二值化,进一步强化边界,增强分离度;同时为腐蚀膨胀做铺垫。
4)腐蚀膨胀处理
腐蚀操作处理图像上小的污点;膨胀操作勾画二维码大致轮廓区域(近似四边形)。
5)Canny边缘检测
Canny边缘检测可以对膨胀处理生成的轮廓区域进行边缘勾画。
6)Hough算子拟合直线
利用Hough算子可以对轮廓边缘线进行近似拟合,生成多个拟合直线。
7)计算二维码四个顶点坐标
利用算法从众多直线中,找到四根边界线,并计算出四个交点(即轮廓四边形顶点)
8)利用顶点坐标进行仿射变换
对四个顶点进行顺时针排序,并按照顶点顺序进行仿射变换。
3. 算法分析(带示例)
1)对比度亮度调整
首先将图片resize到500x500,减小后续图片处理的计算量。随后可以通过对比度因子和亮度因子,对对比度及亮度进行调整。
String srcImagePath( "./result/test.jpg" ); // 原图路径
Mat srcImage;
srcImage = imread( srcImagePath, IMREAD_COLOR ); // 载入初始图片
resize(srcImage, srcImage, Size(500, 500)); //图片缩放为500*500进行后续计算
imwrite("./result/Src_Image.jpg", srcImage); //保存图片
Mat contrastImage = Mat::zeros( srcImage.size(), srcImage.type() ); //亮度与对比度调节
double alpha = 1.8; //对比度因子
int beta = -30; //亮度因子
for( int y = 0; y < srcImage.rows; y++ ) {
for( int x = 0; x < srcImage.cols; x++ ) {
for( int c = 0; c < 3; c++ ) {
contrastImage.at<Vec3b>(y,x)[c] =
saturate_cast<uchar>( alpha*( srcImage.at<Vec3b>(y,x)[c] ) + beta );
}
}
}
imwrite("./result/Contrast_Image.jpg", contrastImage);
2)滤波降噪
将对比度调整后的图片进行灰度转化,降低通道数。随后对该灰度图进行滤波,主要作用是为了降低噪声。不同的噪声类型,可以采用不用的滤波方法,包括高斯滤波、中值滤波、甚至自定义滤波方法。这里我采用的是双边滤波,保留边缘信息。
Mat grayImage;
cvtColor( contrastImage, grayImage, COLOR_BGR2GRAY ); //转化为灰度图
imwrite("./result/Gray_Image.jpg", grayImage); //保存灰度图
Mat filterImage;
bilateralFilter( grayImage, filterImage, 13, 26, 6 ); //双边滤波
//medianBlur ( grayImage, filterImage, 3 ); //中值滤波
imwrite("./result/Filter_Image.jpg", filterImage); //保存滤波后图片
3)反二值化
二值化这一步,将二维码部分与背景进一步分离。同时对结果进行反色,即二维码黑色部分变成白色,背景变成黑色,以便于对后续图像进行腐蚀膨胀等操作。
Mat binaryImage;
threshold( filterImage, binaryImage, 210, 255, THRESH_BINARY_INV ); //反二值化
imwrite("./result/Binary_Image.jpg", binaryImage); //保存二值化图片
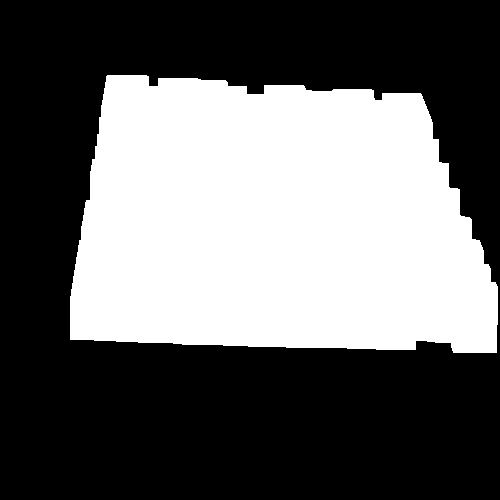
4)腐蚀膨胀处理
首先通过一到两次的腐蚀处理,原本图像上非二维码区域的小污点将被清理掉;随后进行多次膨胀操作,勾画二维码所在位置的大致区域,表现为一个近似的四边形。
Mat erodeImage;
erode( binaryImage, erodeImage, Mat(), Point(-1, -1), 2 ); //腐蚀化
imwrite("./result/Erode_Image.jpg", erodeImage);
Mat dilateImage;
dilate( erodeImage, dilateImage, Mat(), Point(-1, -1), 19 ); //膨胀化
imwrite("./result/Dilate_Image.jpg", dilateImage);
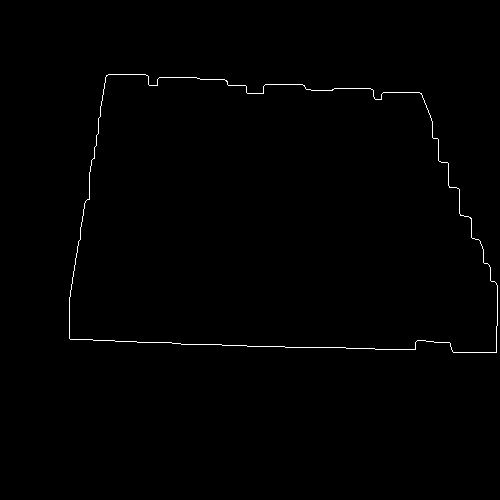
5)Canny边缘检测
利用Canny算法对上述结果进行边缘检测,勾勒出近似四边形的边界。
Mat cannyImage;
Canny( dilateImage, cannyImage, 10, 100, 3, false); //canny边缘检测
imwrite("./result/Canny_Image.jpg", cannyImage);
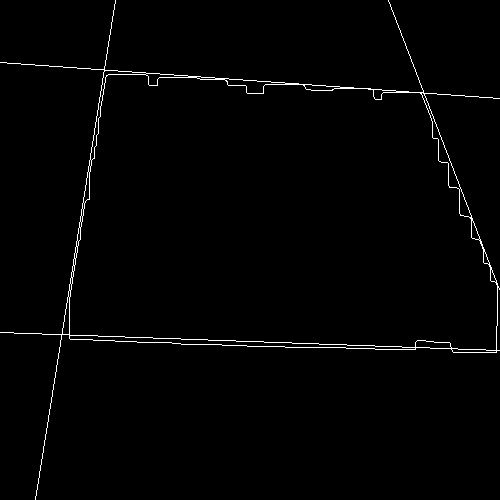
6)Hough算子拟合直线
利用Hough算子对上述结果图进行直线拟合,找到近似四边形的所有近似边的直线,并画出所有直线。(可以通过修改参数以提高或者降低拟合程度,保证每条边至少能拟合一条直线)
//********在canny图上画出所有hough拟合直线
Mat allLinesImage = cannyImage.clone();
vector<Vec2f> lines;
HoughLines( allLinesImage, lines, 5, CV_PI/180, 100 ); //hough算子拟合直线
for( size_t i = 0; i < lines.size(); i++ )
{
float rho = lines[i][0];
float theta = lines[i][1];
double a = cos(theta), b = sin(theta);
double x0 = a*rho, y0 = b*rho;
Point pt1(cvRound(x0 + 1000*(-b)),
cvRound(y0 + 1000*(a)));
Point pt2(cvRound(x0 - 1000*(-b)),
cvRound(y0 - 1000*(a)));
line( allLinesImage, pt1, pt2, Scalar(255), 1, 8 );
}
imwrite("./result/AllLines_Image.jpg", allLinesImage);
7)计算二维码四个顶点坐标
这里分为两个步骤:
1. 从所有直线中,删除相似的直线,保留差距较大的直线。依此得到符合要求的四条边。
其算法思路就是:对所有直线进行两两比较,如果某两条直线角度(theta)之差以及距离原点距离(rho)之差都分别小于某一阈值,则认为这两条直线相似,需要删去其中一条直线。比较完毕后,若发现剩余直线数量大于4,则提高阈值(相反,小于4,则适当降低阈值),继续进行新一轮的比较算法,直到剩余直线数量为4。
//********删除相似直线直到只剩4条拟合直线
double A = 50.0; //初始距离阈值:50
double B = CV_PI / 180 * 20; //初始角度阈值:20度
vector<Vec2f> resLines (lines);
set<size_t> removeIndex; //记录需要删除的直线编号
int countLess4 = 0; //死循环检测
int countMore4 = 0; //死循环检测
while(1){
for( size_t i = 0; i < resLines.size(); i++ ){
for( size_t j = i+1; j < resLines.size(); j++ ){
float rho1 = resLines[i][0];
float theta1 = resLines[i][1];
float rho2 = resLines[j][0];
float theta2 = resLines[j][1];
//theta大于pi,减去进行统一
if(theta1 > CV_PI) theta1 = theta1 - CV_PI;
if(theta2 > CV_PI) theta2 = theta2 - CV_PI;
//记录需要删除的lines(依据角度之差和距离之差)
bool thetaFlag = abs(theta1 - theta2) <= B ||
(theta1 > CV_PI/2 && theta2 < CV_PI/2 && CV_PI - theta1 + theta2 < B) ||
(theta2 > CV_PI/2 && theta1 < CV_PI/2 && CV_PI - theta2 + theta1 < B) ;
if(abs( abs(rho1) - abs(rho2) ) <= A && thetaFlag){
removeIndex.insert( j );
}
}
}
//删除多余的lines
vector<Vec2f> res;
for (int i = 0; i < resLines.size(); i++) {
if( removeIndex.count(i) == 0){
res.push_back(resLines[i]);
}
}
resLines = res;
//直到删除只剩4条直线。
if(resLines.size() > 4){
A = A + 4;
B = B + 2 * CV_PI / 180;
countMore4 ++;
if(countMore4 % 50 == 0)
cout << "countMore4:" << countMore4 << endl;
} else if (resLines.size() < 4) {
B = B - CV_PI / 180;
countLess4 ++;
if(countLess4 % 50 == 0)
cout << "countLess4:" << countLess4 << endl;
}else {
cout << "删除后的剩余直线个数:" << resLines.size() << endl;
break;
}
}
2. 依据找到的四条直线,计算出四边形的四个顶点坐标
算法思路就是:利用直线交点公式,求出所有不同直线的交点。为了得到四个顶点,仅需要求出领边交点即可,因此对于对边的交点,我们需要通过一定手段进行排除。我们发现,四边形的对边一般相交于图片界面外非常远的位置,因此我们可以对交点加以范围限制,以找到符合要求的四个交点。这里我将交点范围设置为图片外延至短边的1/5,超出这个范围,则认为是对边的交点。(当然这种思路还是不适合一些比较极端的案例,欢迎大神提出更好的办法)

//********求出四条定位直线在图像界内的四个交点。
double threshold = 0.2 * min(1.0*srcImage.rows,1.0*srcImage.cols);
vector<Point> points;
for (int i = 0; i < fourLines.size(); i++) {
for (int j = i + 1; j < fourLines.size(); j++) {
double rho1 = fourLines[i][0];
double theta1 = fourLines[i][1];
double rho2 = fourLines[j][0];
double theta2 = fourLines[j][1];
//消除theta等于零导致斜率无法计算的情况
if(theta1 == 0) theta1 = 0.01;
if(theta2 == 0) theta2 = 0.01;
double a1 = cos(theta1), a2 = cos(theta2);
double b1 = sin(theta1), b2 = sin(theta2);
double x = (rho2*b1 - rho1*b2) / (a2*b1 - a1*b2); //直线交点公式
double y = (rho1 - a1*x) / b1;
Point pt(cvRound(x), cvRound(y));
if(pt.x <= srcImage.cols + threshold && pt.x >= 0 - threshold
&& pt.y < srcImage.rows + threshold && pt.y >= 0 - threshold) {
points.push_back(pt);
}
}
}
8)利用顶点坐标进行仿射变换
这里同样分为两个步骤:
1. 依据计算出的四个顶点坐标,对四个坐标进行顺时针排序
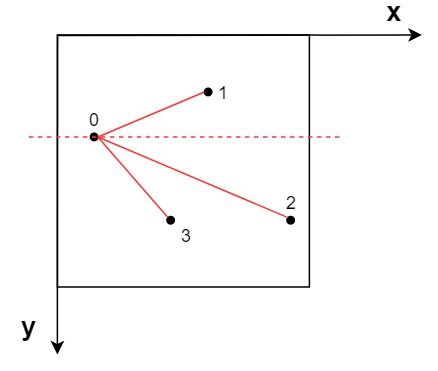
其算法思路就是:首先根据横坐标找到最左边顶点,以这个顶点作为排序起点;随后依次求出该点与其余所连直线的斜率(Δy/Δx),按照斜率从小到大,依次进行排列即可。如图,即排序为0,1,2,3。
//********将获取到的四个交点按顺时针排序并保存在sortPoints中
Point sortPoints[4];
double min_x = 99999.9; //Max_value
int index = -1;
for (int i = 0; i < points.size(); i++) {
if(min_x > points[i].x){
min_x = points[i].x;
index = i;
}
}
Point left = points[index];
points.erase(points.begin()+ index); //删除第index个元素
sortPoints[0] = left;
int autonum = 1;
while (points.size() != 0){
double mingrad = 99999.9; //Max_value
int idx = -1;
for (int i = 0; i < points.size(); i++) {
double curgrad = (points[i].y - left.y)*1.0 / (points[i].x - left.x);
if(mingrad > curgrad){
mingrad = curgrad;
idx = i;
}
}
sortPoints[autonum ++] = points[idx];
points.erase(points.begin()+ idx); //移除当前最小斜率点
}
2. 依据四个顶点,按照顺序进行仿射变换
需要注意的是,仿射变换的映射模型,需要原始的顺时针点对应变换后的顺时针点,即0123对应左上、右上、左下、右下。
//********按照sortPoints四个点进行仿射变换
int minSide = min(srcImage.rows,srcImage.cols);
int center_x = srcImage.rows / 2;
int center_y = srcImage.cols / 2;
Point2f srcTri[4];
Point2f dstTri[4];
srcTri[0] = Point2f( sortPoints[0].x, sortPoints[0].y );
srcTri[1] = Point2f( sortPoints[1].x, sortPoints[1].y );
srcTri[2] = Point2f( sortPoints[2].x, sortPoints[2].y );
srcTri[3] = Point2f( sortPoints[3].x, sortPoints[3].y );
dstTri[0] = Point2f( center_x - 0.45*minSide, center_y - 0.45*minSide );
dstTri[1] = Point2f( center_x + 0.45*minSide, center_y - 0.45*minSide );
dstTri[2] = Point2f( center_x + 0.45*minSide, center_y + 0.45*minSide );
dstTri[3] = Point2f( center_x - 0.45*minSide, center_y + 0.45*minSide );
// 底色图片
Mat perspImage = Mat::zeros(srcImage.rows , srcImage.cols, srcImage.type());
// 提取图像映射模型
Mat transmtx = getPerspectiveTransform(srcTri, dstTri);
Mat binImage;
bitwise_not(binaryImage, binImage); //二值图像反色
//对二值化图像进行仿射变换
warpPerspective(binImage, perspImage, transmtx, perspImage.size());
imwrite("./result/Persp_Image.jpg", perspImage);
4. 完整代码(cpp)
java和python代码思路基本一样。
#include 5. 测试图片
6. 参考资料
OpenCV Java 实现票据、纸张的四边形边缘检测与提取、摆正
opencv——检测四边形的四个角点