DataWhale计算机视觉基础-图像处理(上) -Task01 零基础小白学习笔记
Datawhale 计算机视觉基础-图像处理(上) -Task1 OpenCV框架与图像插值算法
参考资料:
DataWhale:https://github.com/datawhalechina/team-learning/blob/master/%E8%AE%A1%E7%AE%97%E6%9C%BA%E8%A7%86%E8%A7%89%E5%9F%BA%E7%A1%80%EF%BC%9A%E5%9B%BE%E5%83%8F%E5%A4%84%E7%90%86%EF%BC%88%E4%B8%8A%EF%BC%89/Task01%20%E5%9B%BE%E5%83%8F%E6%8F%92%E5%80%BC%E7%AE%97%E6%B3%95.md
学习过程中,参考的一些资料链接:https://www.jianshu.com/p/21eff39af5ad
1.1 简介
- 在图像处理中,平移变换、旋转变换以及放缩变换是一些基础且日常的操作。这些几何变换并不改变图象的像素值,只是在像素平面上进行像素的重新排列。
- 在一幅插入图象 [ u , v ] [u,v] [u,v]中,灰度值仅在整数位置上有定义。然而,输出图象[x,y]的灰度值一般由处在非整数坐标上的 ( u , v ) (u,v) (u,v)值来决定。这就需要插值算法来进行处理。
- 常见的插值算法有最近邻插值、双线性插值和三次样条插值。
1.2 算法理论介绍及推荐
1.2.1 最近邻插值算法原理
- 最近邻插值,是将目标图象中的点,对应到源图像中后,找到最相邻的整数点,作为插值后的输出。
- 假如现在有3x3的图象,现在要放大到4x4。那么,原图象是3x3,目标图象是4x4。
- 用 f ( x , y ) f(x, y) f(x,y)表示目标图像, h ( x , y ) h(x, y) h(x,y)表示原图像,我们有如下公式:
f ( d s t X , d s t Y ) = h ( d s t X s r c W i d t h d s t W i d t h , d s t Y s r c H e i g h t d s t H e i g h t ) \begin{array}{c} f(dst_{X}, dst_{Y}) = h(\frac{dst_{X}src_{Width}} {dst_{Width}}, \frac{dst_{Y}src_{Height}} {dst_{Height}}) \end{array} f(dstX,dstY)=h(dstWidthdstXsrcWidth,dstHeightdstYsrcHeight)
先获得缩放倍数:
K = a m = b m K = \frac{a}{m} = \frac{b}{m} K=ma=mb
现在取目标图象中的点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),可以知道对应原图象中的理论计算位置为:
( x 0 × m a , y 0 × n b ) (\frac{x_0 \times m}{a} , \frac {y_0 \times n}{b} ) (ax0×m,by0×n)
上式得出来的原图象坐标值显然可能是小数,这代表该点在原图象中无实际对应点。那就应该对其四舍五入,将原图像中距离该理论点最近的一个点当作目标图象中的点。这就是最近邻插值。
示例:
f ( 0 , 0 ) = h ( 0 , 0 ) , f ( 0 , 1 ) = h ( 0 , 0.75 ) = h ( 0 , 1 ) , f ( 0 , 2 ) = h ( 0 , 1.50 ) = h ( 0 , 2 ) , f ( 0 , 3 ) = h ( 0 , 2.25 ) = h ( 0 , 2 ) . . . \begin{array}{c} f(0,0)=h(0,0) , \ f(0,1)=h(0,0.75)=h(0,1), \ f(0,2)=h(0,1.50)=h(0,2), \ f(0,3)=h(0,2.25)=h(0,2) \ ...\ \end{array} f(0,0)=h(0,0), f(0,1)=h(0,0.75)=h(0,1), f(0,2)=h(0,1.50)=h(0,2), f(0,3)=h(0,2.25)=h(0,2) ...
缺点:用该方法作放大处理时,在图象中可能出现明显的块状效应。
1.2.2 双线性插值
线性插值多项式: f ( x ) = a 1 x + a 0 f(x)=a_{1} x+a_{0} f(x)=a1x+a0
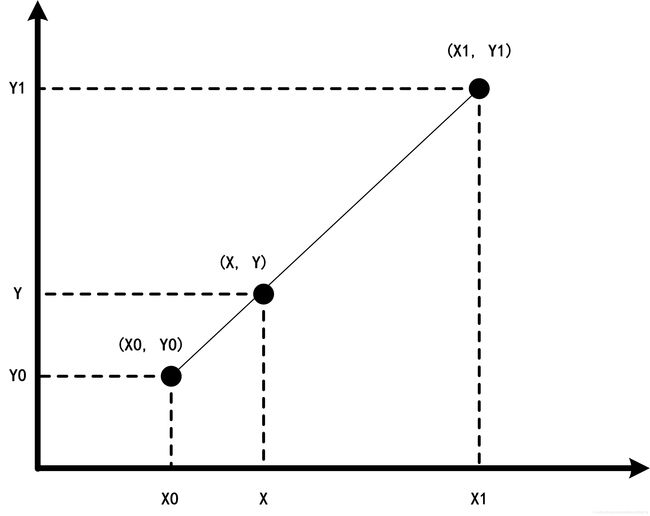
y = y 0 + ( x − x 0 ) y 1 − y 0 x 1 − x 0 = y 0 + ( x − x 0 ) y 1 − ( x − x 0 ) y 0 x 1 − x 0 y=y_{0}+\left(x-x_{0}\right) \frac{y_{1}-y_{0}}{x_{1}-x_{0}}=y_{0}+\frac{\left(x-x_{0}\right) y_{1}-\left(x-x_{0}\right) y_{0}}{x_{1}-x_{0}} y=y0+(x−x0)x1−x0y1−y0=y0+x1−x0(x−x0)y1−(x−x0)y0
y = x 1 − x x 1 − x 0 y 0 + x − x 0 x 1 − x 0 y 0 y= \frac{x_1 - x}{x_1 - x_0} y_0 + \frac {x - x_0}{x_1 - x_0} y_0 y=x1−x0x1−xy0+x1−x0x−x0y0
可以理解为用 x x x和 x 0 , x 1 x_0 , x_1 x0,x1的距离作为一个权重,用于 y 0 y_0 y0和 y 1 y_1 y1的加权。
令 f ( x , y ) f(x,y) f(x,y)为两个变量的函数,其在单位正方形顶点的值已知。假设我们希望通过插值得到正方形内任意点的函数值。则可由双线性方程: f ( x , y ) = a x + b y + c x y + d f(x, y)=a x+b y+c x y+d f(x,y)=ax+by+cxy+d
来定义的一个双曲抛物面与四个已知点拟合。
首先对顶端的两个顶点(0,0)(1,0)进行线性插值得:
f ( x , 0 ) = f ( 0 , 0 ) + x [ f ( 1 , 0 ) − f ( 0 , 0 ) ] f(x, 0)=f(0,0)+x[f(1,0)-f(0,0)] f(x,0)=f(0,0)+x[f(1,0)−f(0,0)]
类似地,再对底端的两个顶点(0,1)(1,1)进行线性插值有: f ( x , 1 ) = f ( 0 , 1 ) + x [ f ( 1 , 1 ) − f ( 0 , 1 ) ] f(x, 1)=f(0,1)+x[f(1,1)-f(0,1)] f(x,1)=f(0,1)+x[f(1,1)−f(0,1)]
最后,做垂直方向(x,0)(x,1)的线性插值,以确定:
f ( x , y ) = f ( x , 0 ) + y [ f ( x , 1 ) − f ( x , 0 ) ] f(x, y)=f(x, 0)+y[f(x, 1)-f(x, 0)] f(x,y)=f(x,0)+y[f(x,1)−f(x,0)]
整理得:
f ( x , y ) = [ f ( 1 , 0 ) − f ( 0 , 0 ) ] x + [ f ( 0 , 1 ) − f ( 0 , 0 ) ] y + [ f ( 1 , 1 ) + f ( 0 , 0 ) − f ( 0 , 1 ) − f ( 1 , 0 ) ] x y + f ( 0 , 0 ) \begin{array}{l} f(x, y)=[f(1,0)-f(0,0)] x+[f(0,1)-f(0,0)] y \ +[f(1,1)+f(0,0)-f(0,1)-f(1,0)] x y+f(0,0) \end{array} f(x,y)=[f(1,0)−f(0,0)]x+[f(0,1)−f(0,0)]y +[f(1,1)+f(0,0)−f(0,1)−f(1,0)]xy+f(0,0)
1.2.3 映射方法
向前映射法
- 可以将几何运算想象成一次一个象素地转移到输出图像中。如果一个输入象素被映射到四个输出像素之间的位置,则其灰度值就按插值算法在4个输出象素之间进行分配。称为向前映射法,或象素移交影射。
- 注:从原图象坐标计算出目标图象坐标镜像、平移变换使用这种计算方法
向后映射法
- 向后映射法(或象素填充算法)是输出象素一次一个地映射回到输入象素中,以便确定其灰度级。如果一个输出象素被映射到4个输入象素之间,则其灰度值插值决定,向后空间变换是向前变换的逆。
- 注:从结果图象的坐标计算原图象的坐标
- 旋转、拉伸、放缩可以使用
- 解决了漏点的问题,出现了马赛克
1.2 基于OpenCV的实现
python
import cv2
img = cv2.imread('xxx.jpg', cv2.IMREAD_UNCHANGED)
print('Original Dimensions : ',img.shape)
Original Dimensions : (1080, 1920, 3)
scale_percent = 30 # percent of original size
width = int(img.shape[1] * scale_percent / 100)
height = int(img.shape[0] * scale_percent / 100)
dim = (width, height)
# resize image
resized = cv2.resize(img, dim, interpolation = cv2.INTER_LINEAR)
cv2.imshow("Resized image", resized)
fx = 1.5
fy = 1.5
resized1 = cv2.resize(resized, dsize=None, fx=fx, fy=fy, interpolation = cv2.INTER_NEAREST)
cv2.imshow("INTER_NEAREST image", resized1)
resized2 = cv2.resize(resized, dsize=None, fx=fx, fy=fy, interpolation = cv2.INTER_LINEAR)
print('Resized Dimensions : ',resized.shape)
cv2.imshow("INTER_LINEAR image", resized2)
cv2.waitKey(0)
cv2.destroyAllWindows()
Resized Dimensions : (324, 576, 3)
可以明显地看出双线性插值解决了最近邻插值的明显块状问题,让图片变得更加平滑和减少失真。
函数原型:
cv2.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]])
参数:
| 参数 | 描述 |
|---|---|
| src | 原图像 |
| dize | 输出图象所需大小 |
| fx | 沿水平轴的比例因子 |
| fy | 沿垂直轴的比例因子 |
| interpolation | 插值方式 |
插值方式:
| interpolation | 名字 |
|---|---|
| cv.INTER_NEAREST | 最近邻插值 |
| cv.INTER_LINEAR | 双线性插值 |
| cv.INTER_CUBIC | 基于4x4像素邻域的3次插值法 |
| cv.INTER_AREA | 基于局部像素的重采样 |
通常,缩小使用cv.INTER_AREA,放缩使用cv.INTER_CUBIC(较慢)和cv.INTER_LINEAR(较快效果也不错)。默认情况下,所有的放缩都使用cv.INTER_LINEAR。
1.3 小结
- 最近邻插值是将原图片上的通过计算对应位置映射到目标图上。因为在计算的过程中,会出现一些点是相同的,所以映射上去有些部分是一样的才会出现图片有块状。
- 双线性插值主要是在目标图片上构建出相应倍数的两条x,y轴。然后在算在对应倍数内x和y在原图片上的大概坐标位置,最后映射到目标图片中。
以上是我对在这次学习中,对两种插值方法的理解。如有误,欢迎来指正~
特别感谢DataWhale组织这次学习!!
Task01 OpenCV框架与图像插值算法 END.
— By: Aaron
博客:https://sandy1230.github.io/
博客:https://blog.csdn.net/weixin_39940512
关于Datawhale:
Datawhale是一个专注于数据科学与AI领域的开源组织,汇集了众多领域院校和知名企业的优秀学习者,聚合了一群有开源精神和探索精神的团队成员。Datawhale以“for the learner,和学习者一起成长”为愿景,鼓励真实地展现自我、开放包容、互信互助、敢于试错和勇于担当。同时Datawhale 用开源的理念去探索开源内容、开源学习和开源方案,赋能人才培养,助力人才成长,建立起人与人,人与知识,人与企业和人与未来的联结。