对极几何、对极点、二次曲线学习心得(持续更新)
对极几何、对极点、二次曲线学习心得
- 用到的线性代数、几何知识
- 反对称矩阵分解
- 矩阵的自由度
- 对极几何基础
- 本质矩阵对极几何
- 本质矩阵的性质
- 本质矩阵的奇异值分解
- 本质矩阵、基础矩阵的自由度
- 极线
- 对极点
- 对极点的性质
- 纯平移运动
- 二次曲线
- 二次曲线的矩阵表达
- 二次曲线的极点和极线
- 二次曲线的极点和极线的矩阵表达
- 二次曲线极线和极点性质举例
- 椭圆
- 对极几何中的二次曲线
- 基础矩阵转化为二次曲线矩阵的作用
- 相关性质
用到的线性代数、几何知识
反对称矩阵分解
任意3X3反对称矩阵 S \bm S S可以分解为 S = k U Z U T {\bm S} = k{\bm U}{\bm Z}{\bm U}^{\rm T} S=kUZUT,其中 U {\bm U} U是正交矩阵,
Z = [ 0 − 1 0 1 0 0 0 0 0 ] {\bm Z}=\left[ \begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right] Z=⎣⎡010−100000⎦⎤
这里 Z {\bm Z} Z也具有一定性质,取
W = [ 0 − 1 0 1 0 0 0 0 1 ] {\bm W} = \left[ \begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right] W=⎣⎡010−100001⎦⎤
则有
Z = [ 1 0 0 0 1 0 0 0 0 ] W {\bm Z} = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right] {\bm W} Z=⎣⎡100010000⎦⎤W
此时,我们可以得到 S = U d i a g { k , k , 0 } W U T {\bm S}={\bm U}diag\{k,k,0\}{\bm W}{\bm U}^{\rm T} S=Udiag{k,k,0}WUT。
矩阵的自由度
矩阵的自由度指的是确定整个矩阵需要确认的最少参数数量。矩阵的自由度具有如下几个性质。
1.一个矩阵的最大自由度是 m × n m\times n m×n;
2.如果一个矩阵是由少于 m × n m\times n m×n个独立参数构成的,则其最大自由度转化为相应的独立参数个数;
3.如果求解这个矩阵的时候这个矩阵还有若干个约束,那么这些约束能组成几个方程,就会给矩阵额外减少几个自由度;
4.若求解矩阵用的方程是齐次方程,由于齐次方程求解内容的尺度等价性,该矩阵会减少一个自由度。
矩阵的自由度决定了求解矩阵参数时所需的最少方程数量,它们是相等的。
对极几何基础
这里主要讲与对极几何相关的,极线、对极点、二次曲线的极线和极点等问题。
本质矩阵对极几何
x 2 T E 21 x 1 = 0 \rm {\bm x}_{2}^{T}{\bm E}_{21}{\bm x}_1 = {\bm 0} x2TE21x1=0
其中, E 21 = t 2 12 ∧ R 21 {\bm E}_{21} = {{\bm t}_{2}^{12}}^{\land}{\bm R}_{21} E21=t212∧R21 是本质矩阵, x 2 {\bm x}_{2} x2 是图2中的一个图像点对应的方向向量, x 1 {\bm x}_1 x1是图1中的一个图像点对应的方向向量,这两个图像点是匹配点,指向同一个三维目标点 X \bm X X。
本质矩阵的性质
本质矩阵的奇异值分解
借助反对称矩阵的性质,我们分解本质矩阵
E 21 = t 2 12 ∧ R 21 = U 21 d i a g { k , k , 0 } W U 21 T R 21 = U 21 d i a g { k , k , 0 } V 21 T \begin{aligned} {\bm E}_{21} & = {{\bm t}_{2}^{12}}^{\land}{\bm R}_{21} \\ & = {\bm U}_{21} diag\{k, k, 0\}{\bm W}{\bm U}_{21}^{\rm T}{\bm R}_{21} \\ & = {\bm U}_{21} diag\{k, k, 0\}{\bm V}_{21}^{\rm T} \end{aligned} E21=t212∧R21=U21diag{k,k,0}WU21TR21=U21diag{k,k,0}V21T
这里 U 21 {\bm U}_{21} U21和 V 21 {\bm V}_{21} V21都是正交矩阵。上述过程是奇异值分解(SVD)过程。
对本质矩阵的奇异值分解不只有唯一解。这是由于该矩阵两个奇异值是相等的,将常数分离出来后,奇异值矩阵转化为 d i a g { I 2 × 2 , 0 } diag\{{\bm I}_{2 \times 2},0\} diag{I2×2,0},单位矩阵则可以转换为任一对正交矩阵和其转置的积,即
E 21 = U 21 d i a g { k , k , 0 } V 21 T = U 21 d i a g { R 2 × 2 , 1 } d i a g { k , k , 0 } d i a g { R 2 × 2 T , 1 } V 21 T \begin{aligned} {\bm E}_{21} & = {\bm U}_{21} diag\{k, k, 0\}{\bm V}_{21}^{\rm T} \\ & = {\bm U}_{21} diag\{{\bm R}_{2\times2},1\} diag\{k, k, 0\}diag\{{\bm R}_{2\times2}^{\rm T},1\}{\bm V}_{21}^{\rm T} \end{aligned} E21=U21diag{k,k,0}V21T=U21diag{R2×2,1}diag{k,k,0}diag{R2×2T,1}V21T
可以看出,本质矩阵奇异值分解后,有效的奇异值矩阵是一个簇。
通过奇异值分解的结果,我们可以看出,本质矩阵的秩是2。
本质矩阵、基础矩阵的自由度
对于一般的三维运动来说, R {\bm R} R和 t {\bm t} t各有3个自由度,因此本质矩阵由定义可得其最大自由度为6。由于求解该矩阵的方程 x 2 T E 21 x 1 = 0 \rm {\bm x}_{2}^{T}{\bm E}_{21}{\bm x}_1 = {\bm 0} x2TE21x1=0是齐次方程,因此本质矩阵具有尺度等价性,减去一个自由度变为5。
对于基础矩阵来说,除了运动的6个自由度以外,还有相机参数的4个自由度,因此两幅图像来自同一个相机时最大自由度是10,来自两个相机时是14,因此该矩阵的最大自由度被限制在9。又由于求解基础矩阵的方程 u 2 T F 21 u 1 = 0 \rm {\bm u}_{2}^{T}{\bm F}_{21}{\bm u}_1 = {\bm 0} u2TF21u1=0是齐次方程,具有尺度等价性,减少1个自由度;此外,基础矩阵也有不满秩的约束,即 d e t ( F 21 ) = 0 det({\bm F_{21}})={\bm 0} det(F21)=0,减少1个自由度。因此基础矩阵有7个自由度。
极线
这里假设 x 1 {\bm x}_{1} x1和 x 2 {\bm x}_{2} x2表示图像点对应的落在归一化平面上的方向向量,即 x 1 = [ x 1 , y 1 , 1 ] T {\bm x}_{1}=[x_1, y_1, 1]^{\rm T} x1=[x1,y1,1]T, x 2 = [ x 2 , y 2 , 1 ] T {\bm x}_{2}=[x_2, y_2, 1]^{\rm T} x2=[x2,y2,1]T。取 x 2 T E 21 = [ l 11 , l 12 , l 13 ] {\bm x}_{2}^{\rm T}{\bm E}_{21}=[l_{11}, l_{12}, l_{13}] x2TE21=[l11,l12,l13],那么这里有
l 11 x 1 + l 12 y 1 + l 13 = 0 l_{11}x_1 + l_{12}y_1 + l_{13} = 0 l11x1+l12y1+l13=0
这是一条在图1归一化平面上面的二维直线,称为极线。对于图2上的极线来说同理。
对极点
这里取向量 t 2 12 {{\bm t}_{2}^{12}} t212与图2的归一化平面交点为 e 2 {\bm e}_2 e2,则 e 2 T E 21 = e 2 T t 2 12 ∧ R 21 = [ e 2 × t 2 12 ] T R 21 = 0 {\bm e}_2^{\rm T}{\bm E}_{21}={\bm e}_2^{\rm T}{{\bm t}_{2}^{12}}^{\land}{\bm R}_{21} =[{\bm e}_2 \times {\bm t}_{2}^{12}]^{\rm T} {\bm R}_{21}=\bm 0 e2TE21=e2Tt212∧R21=[e2×t212]TR21=0
因此不论图1上哪个点与之点乘都得到零。 e 2 {\bm e}_2 e2被称为图2上的对极点,同理 e 1 {\bm e}_1 e1是图1上的对极点。
对极点的性质
图2上任一点的极线都会经过图1上的对极点,同理图1上任一点的极线都会经过图2上的对极点。
一个三维点相对于图1的深度越大,在图2上对应的极线上,对应的位置越偏离对极点。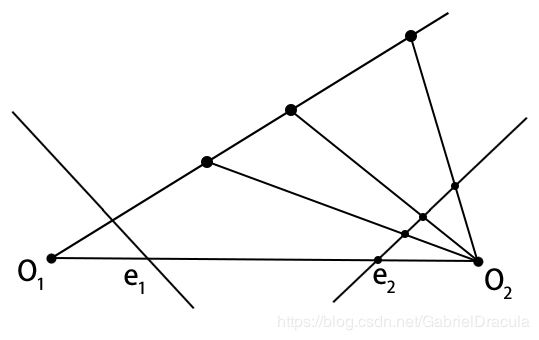
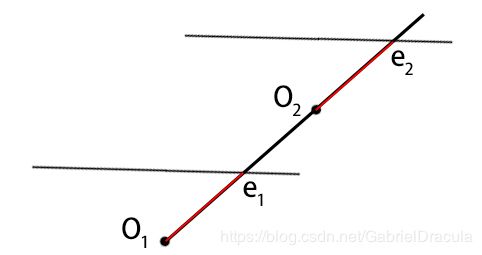
纯平移运动
纯平移运动中,两张图的对极点相对于各自的相机坐标系的坐标是相同的。
二次曲线
二次曲线在中学学习时被称为圆锥曲线,实际上,中学里学过的圆、椭圆、双曲线、抛物线都属于二次曲线,但二次曲线不都是圆锥曲线。本部分引用了知乎答案。
【解析几何】什么是极线,好吃吗? - Dylaaan的文章 - 知乎
https://zhuanlan.zhihu.com/p/33873965
以下所有内容均为二维二次曲线的内容,三维二次曲线对各个方阵、向量扩展z轴即可。
二次曲线的矩阵表达
一般来说,平面上的二维二次曲线都可以表达成
[ x y 1 ] [ A B C B D E C E F ] [ x y 1 ] = 0 \left[ \begin{array}{ccc} x & y & 1 \end{array} \right] \left[ \begin{array}{ccc} A & B & C \\ B & D & E \\ C & E & F \end{array} \right] \left[ \begin{array}{c} x \\ y \\ 1 \end{array} \right] = \bm 0 [xy1]⎣⎡ABCBDECEF⎦⎤⎣⎡xy1⎦⎤=0
例如,圆的表达式为
[ x y 1 ] [ 1 0 − a 0 1 − b − a − b r 2 − a 2 − b 2 ] [ x y 1 ] = 0 \left[ \begin{array}{ccc} x & y & 1 \end{array} \right] \left[ \begin{array}{ccc} 1 & 0 & -a \\ 0 & 1 & -b \\ -a & -b & r^2-a^2-b^2 \end{array} \right] \left[ \begin{array}{c} x \\ y \\ 1 \end{array} \right] = \bm 0 [xy1]⎣⎡10−a01−b−a−br2−a2−b2⎦⎤⎣⎡xy1⎦⎤=0
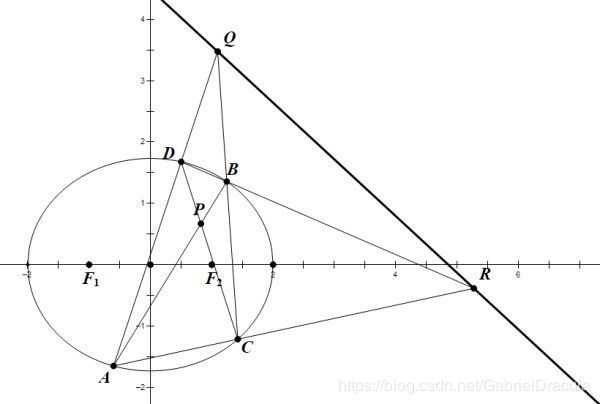
二次曲线的极点和极线
对于任意一个点 P {\bm P} P,做两条直线 A B {\bm A}{\bm B} AB, C D {\bm C}{\bm D} CD,均与二次曲线有两个交点,分别是 A , B , C , D {\bm A},{\bm B},{\bm C},{\bm D} A,B,C,D。取 A C {\bm A}{\bm C} AC与 B D {\bm B}{\bm D} BD的交点为 R {\bm R} R, A D {\bm A}{\bm D} AD与 B C {\bm B}{\bm C} BC的交点为 Q {\bm Q} Q,定义 Q R {\bm Q}{\bm R} QR为极点 P {\bm P} P的极线。
二次曲线的极点和极线的矩阵表达
对于一个二维点 P = [ x 0 y 0 1 ] T {\bm P}=\left[ \begin{array}{ccc} x_0 & y_0 & 1\end{array} \right] ^{\rm T} P=[x0y01]T (此处坐标为齐次坐标)和一个二次曲线,直线
[ x 0 y 0 1 ] [ A B C B D E C E F ] [ x y 1 ] = 0 \left[ \begin{array}{ccc} x_0 & y_0 & 1 \end{array} \right] \left[ \begin{array}{ccc} A & B & C \\ B & D & E \\ C & E & F \end{array} \right] \left[ \begin{array}{c} x \\ y \\ 1 \end{array} \right] = \bm 0 [x0y01]⎣⎡ABCBDECEF⎦⎤⎣⎡xy1⎦⎤=0
被称为二次曲线在极点 P {\bm P} P处的极线。
二次曲线极线和极点性质举例
椭圆
当极点在椭圆上,极线为椭圆在极点处的切线;
当极点在椭圆外,极线与椭圆的两个交点与极点之间的两条连线分别为椭圆在两个交点处的切线;
当极点在椭圆内,过极点做一条直线与椭圆相交于两点,这两点处椭圆的切线的交点一定在极线上。
对极几何中的二次曲线
对于一个基本矩阵 E {\bm E} E,我们将其分解为一个对称矩阵 E s {\bm E_s} Es和一个反对称矩阵 E a {\bm E_a} Ea: E = E s + E a {\bm E} = {\bm E_s} + {\bm E_a} E=Es+Ea,有
E s = E + E T 2 , E a = E − E T 2 {\bm E_s}=\frac{{\bm E} + {\bm E}^{\rm T}}{2}, {\bm E_a}=\frac{{\bm E} - {\bm E}^{\rm T}}{2} Es=2E+ET,Ea=2E−ET
反对称矩阵等价于一个三维向量的叉乘矩阵,所以我们取 E a = x a ∧ {\bm E_a}={\bm x_a}^{\land} Ea=xa∧,且对于任意三维向量 x {\bm x} x都有 x T E a x = 0 {\bm x}^{\rm T}{\bm E_a}{\bm x}=\bm 0 xTEax=0。
此时,二次曲线 E 21 s {\bm E_{21s}} E21s在极点 x 21 a {\bm x_{21a}} x21a处的极线为对极点 e 1 {\bm e_1} e1和 e 2 {\bm e_2} e2的连线。
基础矩阵转化为二次曲线矩阵的作用
首先定义同视点。同视点是在两帧图像中,具有相同坐标的点。对于同视点,有
x T E 21 x = x T E 21 s x + x T E 21 a x = x T E 21 s x = 0 {\bm x}^{\rm T}{\bm E_{21}}{\bm x} = {\bm x}^{\rm T}{\bm E_{21s}}{\bm x} + {\bm x}^{\rm T}{\bm E_{21a}}{\bm x} \\ = {\bm x}^{\rm T}{\bm E_{21s}}{\bm x} =\bm 0 xTE21x=xTE21sx+xTE21ax=xTE21sx=0
因此,这些同视点构成一个二次曲线。
相关性质
当我们要求二次曲线 E 21 s {\bm E_{21s}} E21s在极点 x \bm x x处的极线时,可以将对极点 e 1 {\bm e_1} e1与 x \bm x x相连得到二次曲线和该直线的另一个交点 x c \bm x_c xc,将 x c \bm x_c xc与对极点 e 2 {\bm e_2} e2相连即为极点 x \bm x x的极线。