常见的五种神经网络(5)-生成对抗网络（上）之变分自动编码器

概率生成模型简称生成模型（Generative Model），是概率统计和机器学习中的一类重要模型，指一系列用于随机生成可观测数据的模型。生成模型的思路是根据可观测的样本学习一个参数化的模型$p_{\theta }(x)$来近似未知分布$p_r(x)$，使得生成的样本和真实的样本尽可能的相似。

深度生成模型就是利用深层神经网络可以近似任意函数的能力来建模一个复杂的分布$p_r(x)$。常见的两种深度生成模型包括变分自动编码器（Variational Autoencoder, VAE）和生成对抗网络（Generative Adversarial Networks, GAN）（因为他们的目标基本是一致的）。本篇内容主要介绍生成模型的基本功能和变分自动编码器。

生成模型的基本功能

生成模型的两个基本功能为：

• 密度估计
• 生成样本

密度估计

给定一组数据$D=\{x^i\},1\le i\le N$，假设他们都是独立地从相同的概率密度函数为$p_r(x)$的未知分布中产生的，密度估计是根据数据集$D$来估计其概率密度函数$p_{\theta }(x)$。

生成模型也可以应用于监督学习，监督学习的目标是建模输出标签的条件概率密度函数$p(y|x)$。根据贝叶斯公式：
$$p(y|x)=\frac{p(x|y)}{{\sum }_{y}p(x,y)}$$
可以将监督学习问题转化为联合概率密度函数p(x,y)的密度估计问题。在监督学习中比较典型的生成模型有朴素贝叶斯分类器、隐马尔可夫模型

和生成模型相对应的另一类监督学习模型是判别模型（Discriminative Model），判别式模型直接建模条件概率密度函数$p(y|x)$，并不建模其联合概率密度函数$p(x,y)$，常见的判别模型有logistic 回归、支持向量机、神经网络等。由生成模型可以得到判别模型，但由判别模型得不到生成模型。

生成样本

生成样本就是给定一个概率密度函数为$p_{\theta }(x)$的分布，生成一些服从这个样本的分布，也称为采样。

对于带隐变量的生成模型，在得到$p(z,\theta )$和$p(x|z,\theta )$之后，就可以生成数据$x$，具体可以分为两步执行：

• 根据隐变量的先验分布$p(z,\theta )$进行采样，得到样本$z$
• 根据条件分布$p(x|z,\theta )$进行采样，得到样本$x$

变分自动编码器

以下内容来自于：https://spaces.ac.cn/archives/5253

从分布变换看VAE

VAE和GAN的目标都是：希望构建一个从隐变量$Z$生成目标数据$X$的模型，但是实现上有所不同。它们假设$Z$服从某些常见的数据分布（正态分布，均匀分布等），然后希望训练得到一个模型$X=g(Z)$，这个模型能够将原来的概率分布映射到训练集的概率分布，即，他们的目的都是进行分布之间的变换。

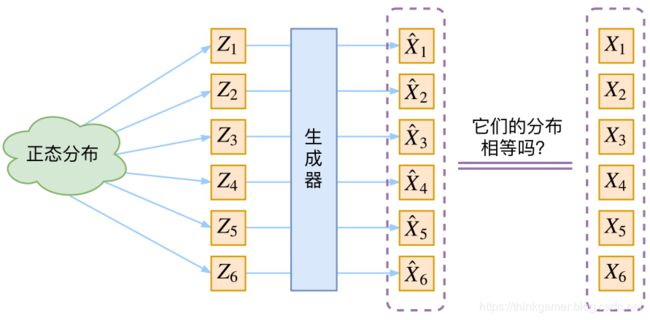
生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式。

VAE的通常理解

首先我们有一批样本$\{X_1,X_2,...,X_n\}$，其整体使用$X$描述，我们本想根据$\{X_1,...,x_n\}$得到$X$的分布$P(X)$，如果能得到的话，我们直接根据$P(X)$来采样，就可以得到所有可能的$X$了。这是一个理想的终极模型，但很难实现，于是将分布改为：
$$p(X)=\sum _{Z}p(X|Z)p(Z)$$
这里不区分求和还是求积分，意思差不多就行。此时$p(X|Z)$就描述了一个由$Z$来生成$X$的模型，而我们假设$Z$服从标准的正态分布，即：$p(Z)=N(0,1)$，如果这个理想能实现，我们就可以先从标准的正态分布中采样一个$Z$，然后根据$Z$来计算$X$，这也是一个很棒的生成模型。接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现，框架结构如下所示：

但是上图存在一个问题：我们不清楚经过重新采样生成的$Z_k$是否还对应着原来的$X_k$，所以直接最小化$D(\widehat{X_k},X_k{)}^2$是很不科学的。而实际上，你看代码，也会发现根本不是这样实现的。

VAE应该是什么样的

其实在整个VAE模型中，并没有使用$p(Z)$（隐变量空间的分布）是正态分布的假设，我们用的是假设$p(X|Z)$（后验分布）是正态分布。

具体来说，给定一个真实样本$X_k$，我们假设存在一个专属于$X_k$的分布$p(Z|X_k)$（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布，这里强调专属因为：后面要训练一个生成器$X=g(Z)$，希望能够把从分布$p(Z|X_k)$采样出来的$Z_k$还原为$X_K$。如果假设$p(Z)$是正态分布，然后从$p(Z)$中采样一个$Z$，那么我们怎么知道这个$Z$是对应哪个真实的$X$呢？现在$p(Z|X_k)$专属于$X_k$，我们有理由说从这个分布采样出来的$Z$应该要还原到$X_k$中去。

事实上，在论文《Auto-Encoding Variational Bayes》的应用部分，也特别强调了这一点。

---

In this case, we can let the
variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:
$$\log q_{\varphi }(\mathbf{z}|{\mathbf{x}}^{(i)})=\log \mathcal{N}(\mathbf{z};{\mathbf{\mu }}^{(i)},{\mathbf{\sigma }}^{2(i)}\mathbf{I})\text{\hspace{1em}(9)}$$
（注：这里是直接摘录原论文，本文所用的符号跟原论文不尽一致，望读者不会混淆。）

---

上面介绍到了，每一个$X_k$都配上了一个专属的正态分布，才方便后续的生成器做还原，但这样有多少个$X$就有多少个正态分布了。我们知道正态分布分布有两组参数$\mu$和${\sigma }^2$，那怎么找出专属$X_k$的正态分布$P(Z|X_k)$的均值和方差呢？并没有什么直接的思路，那么就用神经网络来拟合吧。

于是我们就可以构建两个神经网络${\mu }_k=f_1(X_k),log{\sigma }^2=f_2(X_k)$来计算均值和方差了。这里之所以选择$log{\sigma }^2$是因为${\sigma }^2$总是非负的，需要加激活函数处理，而拟合$log{\sigma }^2$不需要加激活函数处理，因为可正可负。到这里，能知道专属于$X_k$的均值和方差了，也知道他的正态分布长什么样子了，然后从一个专属分布中采样一个$Z_k$出来，然后经过一个生成器得到$\widehat{X_k}=g(Z_k)$，现在可以放心的最小化$D(\widehat{X_k},X_k{)}^2$，因为$Z_k$是从专属的$X_k$的分布中采样出来的，这个生成器要把开始的$X_k$还原回来，于是可以画出VAE的示意图为：

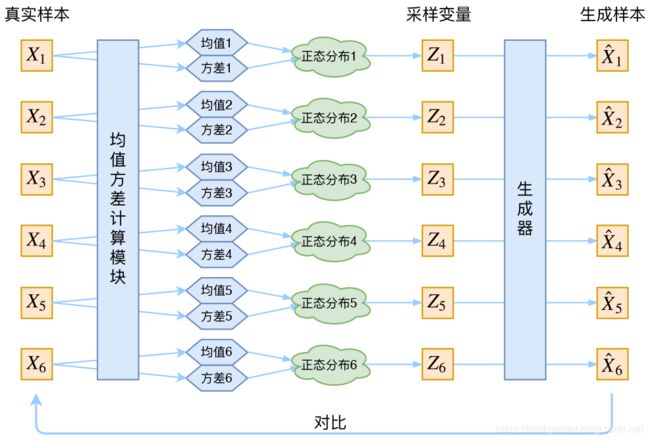
分布标准化

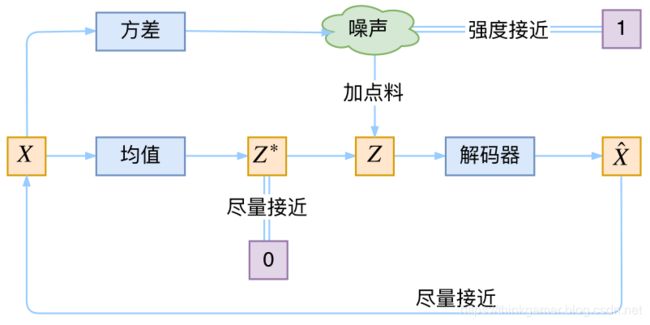
首先，我们希望重构$X$，也就是最小化$D(\widehat{X_k},X_k{)}^2$，但这个过程容易收到噪声的影响，因为$Z_k$是经过重新采样生成的，不是直接由encoder算出来的。显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差）通过一个神经网络算出来的，所以最终模型为了重构的更好，肯定会想尽办法让方差变为0，而方差为0的话，也就没有随机性了，所以不管怎么样采样都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。

说白了，模型会慢慢退化成普通的AutoEncoder，噪声不再起作用。那这样的话，就不是生成模型。

其实VAE还让所有的$p(Z|x)$都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。如下图所示：

那么如何让所有的$p(Z|X)$都向$N(0,1)$看齐呢？原论文直接算了一般（各分量独立的）正态分布与标准正态分布的KL散度$KL(N(\mu ,{\sigma }^2)||N(0,1))$作为这个额外的loss，计算结果为：
$${\mathcal{L}}_{\mu ,{\sigma }^2}=\frac{1}{2}\sum _{i=1}^d({\mu }_{(i)}^2+{\sigma }_{(i)}^2-\log {\sigma }_{(i)}^2-1)\text{\hspace{1em}(4)}$$

这里的$d$指的是隐变量$Z$的维度，而${\mu }_i$和${\sigma }_i^2$分别代表一般正态分布的均值向量和方差向量的第$i$个分量。直接用这个公式做补充loss，就不用考虑均值损失和方差损失的相对比例问题了。

VAE的本质

VAE虽然也是AE（AutoEncoder）的一种，但他的做法是独特的，在VAE中，他的Encoder有两个，一个用来计算均值，一个用来计算方差。

VAE从让普通人望而生畏的变分和贝叶斯理论出发，最后落地到一个具体的模型中，虽然走了比较长的一段路，但最终的模型其实是很接地气的：他本质上就是在我们常规的自编码器的基础上，对encoder的结果加上了“高斯噪声”，使得结果decoder能够对噪声有鲁棒性，而那个额外的KL loss事实上就是相当于encoder的一个正则项，希望encoder出来的东西均有零均值。

那另外一个encoder的作用是用来动态调节噪声的强度的，直觉上想，当decoder还没有训练好的时候（重构误差远大于KL loss），就会适当降低噪声（KL loss增加），使得拟合起来更加容易一些（重构误差开始下降）；反之，如果decoder训练得还不错时（重构误差小于KL loss），这时候噪声就会增加（KL loss减少），使得拟合更加困难了（重构误差又开始增加），这时候decoder就要想办法提高他的生成能力了。

说白了，重构的过程是希望没噪声的，而KL loss则希望有高斯噪声的，两者是对立的，所以VAE跟GAN一样，内部其实时包含了一个对抗的过程，只不过他们两者是混合起来，共同进化的。

VAE中的变分

VAE叫做“变分自编码器”，他跟变分法有什么联系？在VAE的论文和相关解读中，好像也没看到变分法的存在呀？

如果大家承认KL散度的话，那VAE好像真的跟变分没多大关系了～因为理论上对于KL散度要证明：

固定概率分布$p(x)（或q(x)）$的情况下，对于任意的概率分布$q(x)（或p(x)）$，都有$KL(p(x)||q(x))\ge 0$，而且只有当$p(x)=q(x)$时才等于零。

因为$KL(p(x)||q(x))$实际上是一个泛函，要对泛函求极值就要用到变分法，当然，这里的变分法只是普通微积分的平行推广，还没涉及到真正复杂的变分法。而VAE的变分下界，是直接基于KL散度就得到的。所以直接承认了KL散度的话，就没变分什么事了。

所有VAE名字中的变分，是因为他的推导过程用到了KL散度及其性质。

至此已经把变分自编码的内容捋的差不多了，再下一篇将会更新GAN！

---

扫一扫 关注微信公众号！号主 专注于搜索和推荐系统，尝试使用算法去更好的服务于用户，包括但不局限于机器学习，深度学习，强化学习，自然语言理解，知识图谱，还不定时分享技术，资料，思考等文章！

---