OpenGL递归细分四面体法绘制球体
OpenGL递归细分四面体绘制球体
递归细分四面体法绘制三维球体,其思路是首先绘制一个内接于单位球体的正四面体,然后递归地分割四面体的平面,所分割的点经过归一化映射到球面上。经过足够多次的递归,就可以用多面体来逼近球体。
1. 递归细分四面体
首先设定初始的四面体:内接于单位球体的正四面体,其四个顶点容易计算,结果如下:
GLfloat tetrahedron_vertex[][3] = {
0.0f, 0.0f, 1.0f,
0.0f, 0.942809f, -0.333333f,
-0.816497f, -0.471405f, -0.333333f,
0.816497f, -0.471405f, -0.333333f
};
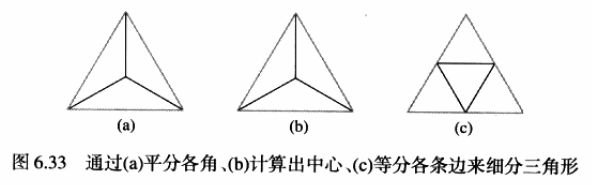
随后要对四面体每个面的三角形进行细分,如下图所示有等分各角、寻找中心以及等分各边等等方式的细分方法,本次代码采用等分各边的方式,将正三角形进一步细分为四个正三角形。细分过后的四个正三角形和原本的三角形仍在同一平面,因此需要通过归一化将其映射到单位球面上:将顶点到原点的距离从原距离放缩到1即可。设定好递归层次数depth之后,开始递归地进行细分,如果没有达到层次数,则进一步细分三角形,如果depth降为0则开始绘制最终的小三角形。这种方式可以通过控制depth的大小来控制最终球面的近似效果。为了直观感受近似效果,本次代码只绘制了近似出的网格线。
void normalize(GLfloat* v)
{
GLfloat d = sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);
v[0] /= d; v[1] /= d; v[2] /= d;
}
void divide_triangle(GLfloat* a, GLfloat* b, GLfloat* c, int depth)
{
if (depth > 0) {
GLfloat ab[3], ac[3], bc[3];
for (unsigned int i = 0; i < 3; i++)
ab[i] = a[i] + b[i];
normalize(ab);
for (unsigned int i = 0; i < 3; i++)
ac[i] = a[i] + c[i];
normalize(ac);
for (unsigned int i = 0; i < 3; i++)
bc[i] = b[i] + c[i];
normalize(bc);
divide_triangle(a, ab, ac, depth - 1);
divide_triangle(b, bc, ab, depth - 1);
divide_triangle(c, ac, bc, depth - 1);
divide_triangle(ab, bc, ac, depth - 1);
}
else {
glBegin(GL_LINE_LOOP);
glColor3f(sqrt(a[0]*a[0]), sqrt(a[1] * a[1]), sqrt(a[2] * a[2]));
glVertex3fv(a);
glVertex3fv(b);
glVertex3fv(c);
glEnd();
}
}
2. 运行效果
下图分别是递归层次设置为3次、4次、6次的球体近似效果:
附录:完整代码
#include
#include
#include
#define DEPTH 4
using namespace std;
GLfloat tetrahedron_vertex[][3] = {
0.0f, 0.0f, 1.0f,
0.0f, 0.942809f, -0.333333f,
-0.816497f, -0.471405f, -0.333333f,
0.816497f, -0.471405f, -0.333333f
};
void normalize(GLfloat* v)
{
GLfloat d = sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);
v[0] /= d; v[1] /= d; v[2] /= d;
}
void divide_triangle(GLfloat* a, GLfloat* b, GLfloat* c, int depth)
{
if (depth > 0) {
GLfloat ab[3], ac[3], bc[3];
for (unsigned int i = 0; i < 3; i++)
ab[i] = a[i] + b[i];
normalize(ab);
for (unsigned int i = 0; i < 3; i++)
ac[i] = a[i] + c[i];
normalize(ac);
for (unsigned int i = 0; i < 3; i++)
bc[i] = b[i] + c[i];
normalize(bc);
divide_triangle(a, ab, ac, depth - 1);
divide_triangle(b, bc, ab, depth - 1);
divide_triangle(c, ac, bc, depth - 1);
divide_triangle(ab, bc, ac, depth - 1);
}
else {
glBegin(GL_LINE_LOOP);
glColor3f(sqrt(a[0]*a[0]), sqrt(a[1] * a[1]), sqrt(a[2] * a[2]));
glVertex3fv(a);
glVertex3fv(b);
glVertex3fv(c);
glEnd();
}
}
void display()
{
// 设置逆时针排列的点围成的平面为正面
glFrontFace(GL_CCW);
// 设置不绘制背面,节省算力同时不会出现背面覆盖正面的情况
glCullFace(GL_BACK);
glEnable(GL_CULL_FACE);
// 设置背景为白色
glClearColor(1.0, 1.0, 1.0, 1.0);
glClear(GL_COLOR_BUFFER_BIT);
// 加载单位阵
glLoadIdentity();
// 设置相机的位置和视角
// 有关gluLookAt:https://blog.csdn.net/Augusdi/article/details/20470813
gluLookAt(2, 2, 2, 0.0, 0.0, 0.0, -1, -1, 1);
divide_triangle(tetrahedron_vertex[0], tetrahedron_vertex[2], tetrahedron_vertex[1], DEPTH);
divide_triangle(tetrahedron_vertex[0], tetrahedron_vertex[3], tetrahedron_vertex[2], DEPTH);
divide_triangle(tetrahedron_vertex[0], tetrahedron_vertex[1], tetrahedron_vertex[3], DEPTH);
divide_triangle(tetrahedron_vertex[1], tetrahedron_vertex[2], tetrahedron_vertex[3], DEPTH);
glutSwapBuffers();
}
// 窗口大小自适应函数,使得窗口大小改变时仍保持图形的比例不变
// 有关窗口自适应函数:http://blog.sina.com.cn/s/blog_5497dc110102w8qh.html
void reshape(int w, int h)
{
glViewport(0, 0, (GLsizei)w, (GLsizei)h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(60.0, (GLfloat)w / (GLfloat)h, 1.0, 20.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(2, 2, 2, 0.0, 0.0, 0.0, -1, -1, 1);
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
// 设置双缓冲和RGB颜色模式
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
// 设置窗口大小、位置和名称
glutInitWindowSize(500, 500);
glutInitWindowPosition(100, 100);
glutCreateWindow("sphere");
// 设置绘制函数、窗口大小自适应函数
glutDisplayFunc(display);
glutReshapeFunc(reshape);
// 进入主循环
glutMainLoop();
return 0;
}