R语言实战笔记 基本统计分析-频数列联表和简单的独立性检验

描述性统计分析

使用车辆路试（mtcars）数据集。关注每加仑汽油行驶英里数（mpg），马力（hp），车重（wt）。

•  

> myvars<-c("mpg","hp","wt")
> head(mtcars[myvars])

其中head只取最前面6行

•  

> summary(mtcars[myvars])

通过summary()计算描述性统计量。summary()函数提供了最小值、最大值、四分位数、和数值型变量的均值，以及因子向量和逻辑型向量的频数统计。

•  

> mystats <- function(x, na.omit=FALSE){
     if (na.omit)
         x <- x[!is.na(x)]
     m <- mean(x)
     n <- length(x)
     s <- sd(x)
     skew <- sum((x-m)^3/s^3)/n
     kurt <- sum((x-m)^4/s^4)/n - 3
     return(c(n=n, mean=m, stdev=s, skew=skew, kurtosis=kurt))
 }
> sapply(mtcars[myvars], mystats)

summary()函数中并没有提供偏度和峰度打的计算函数，可以使用sapply()添加类似平均值、标准差、分布等特征。

•  

> myvars<-c("mpg","hp","wt")
> aggregate(mtcars[myvars],by=list(am=mtcars$am),mean)
> aggregate(mtcars[myvars],by=list(am=mtcars$am),sd)

如图，mtcars中的数据，am是的取值只有1和0两种，aggregate()方法得到的结果是am分别为0或者1时，我们选中的mpg、hp、wt值的mean（平均值）或者sd（标准差）。

 

•  aggregate() 仅允许在每次调用中使用平均数、标准差这样的单返回值函数。它无法一次返回若干个统计量。要完成这项任务，可以使用 by() 函数。

by(data, INDICES, FUN)

其中 data 是一个数据框或矩阵， INDICES 是一个因子或因子组成的列表，定义了分组， FUN 是任意函数。

> dstats <- function(x)sapply(x, mystats)
> myvars <- c("mpg", "hp", "wt")
> by(mtcars[myvars], mtcars$am, dstats)

这里dstats()调用了mystats()函数，将其应用于数据框中的每一栏，在通过by()函数则可得到am中每一水平的概括统计量。

 

频数表和列联表

数据准备

  本节中的数据来自 vcd 包中的 Arthritis 数据集。这份数据来自Kock & Edward （1988），表示了一项风湿性关节炎新疗法的双盲临床实验的结果。

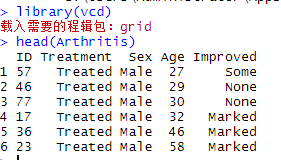
> library(vcd)
> head(Arthritis)

治疗情况（安慰剂治疗、用药治疗）、性别（男性、女性）和改善情况（无改善、一定程度的改善、显著改善）均为类别型因子。

生成频数表

• 一维列联表

记录的是Improved的频数。

然后通过prop.table()将频数转换为比例值。

或者pro.table()*100转化为百分比。

> library(vcd)
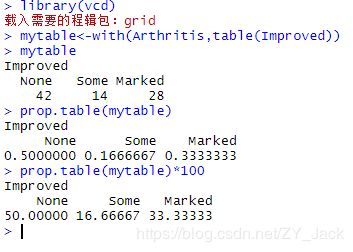
> mytable<-with(Arthritis,table(Improved))
> mytable
> prop.table(mytable)
> prop.table(mytable)*100

• 二维列联表

> mytable <- xtabs(~ A + B, data=mydata)

其中的 mydata 是一个矩阵或数据框。总的来说，要进行交叉分类的变量应出现在公式的右侧（即~ 符号的右方），以 + 作为分隔符。若某个变量写在公式的左侧，则其为一个频数向量（在数据已经被表格化时很有用）。

• 可以使用 margin.table() 和 prop.table() 函数分别生成边际频数和比例。

下面是行和行比例

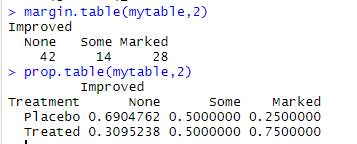
> margin.table(mytable, 1)
> prop.table(mytable, 1)

观察表格可以发现，与接受安慰剂的个体中有显

著改善的16%相比，接受治疗的个体中的51%的个体病情有了显著的改善。

 

下面是列和列比例

> margin.table(mytable,2)
> prop.table(mytable,2)

 

• 为表格添加边际和。（分为为所有变量添加，为行添加和为列添加三种）

> addmargins(prop.table(mytable))

> addmargins(prop.table(mytable, 1), 2)

> addmargins(prop.table(mytable, 2), 1)

 

 

使用CrossTable()函数生成二维列联表

> library(gmodels)
> CrossTable(Arthritis$Treatment,Arthritis$Improved)

如图，第3，4，5行分别是行比例，列比例和总比例

多维列联表

> mytable<-xtabs(~Treatment+Sex+Improved, data = Arthritis)
> mytable

可以通过以下命令来探究边际频数和比例等的详细信息。

> ftable(prop.table(mytable,c(1,2)))
> ftable(addmargins(prop.table(mytable, c(1, 2)), 3))

 

 

独立性检验 

卡方独立性检验​​​​​​

• 判断治疗情况和改善情况是否独立

> mytable<-xtabs(~Treatment+Improved,data = Arthritis)
> chisq.test(mytable)

 可见结果不独立。

• 判断性别和改善的情况是否独立

> mytable<-xtabs(~Improved+Sex,data = Arthritis)
> chisq.test(mytable)

（附上P值的意义：P值 (P-value) P值，也就是常见到的 P-value。P 值是一种概率，指的是在 H0 假设为真的前提下，样本结果出现的概率。如果 P-value 很小，则说明在原假设为真的前提下，样本结果出现的概率很小，甚至很极端，这就反过来说明了原假设很大概率是错误的。通常，会设置一个显著性水平（significance level） α\alphaα 与 P-value 进行比较，如果 P-value < α\alphaα ，则说明在显著性水平 α\alphaα 下拒绝原假设，α\alphaα 通常情况下设置为0.05。）

 

 

Fisher精确检验

使用fisher.test(mytable)函数进行Fisher精确检验，mytable是一个二维列联表。

> mytable<-xtabs(~Treatment+Improved,data = Arthritis)
> fisher.test(mytable)

这里的fisher.test()可以在任意行列数大于等于2的二维列联表上使用，但不能用于2*2的列联表。 

 

 

Cochran-Mantel-Haenszel检验

Mantelhan.test()函数可用来进行Cochran-Mantel-Haenszel卡方检验。原假设是，两个名义变量在第三个变量的每一层中都是条件独立的。

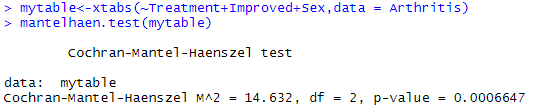
> mytable<-xtabs(~Treatment+Improved+Sex,data = Arthritis)
> mantelhaen.test(mytable)

结果表明，患者接受的治疗与得到的改善在性别的每一水平下并不独立（分性别来看，用药的患者比接受安慰剂的患者游乐更多的改善） 

 

 

相关性的度量

通过vcd包中的assocstats()函数可以用来计算二维列联表的phi系数、列联系数和Cramer’s V系数。

> library(vcd)
> mytable<-xtabs(~Treatment+Improved,data = Arthritis)
> assocstats(mytable)

总体来说，较大的值意味着较强的相关性。

 

还可以采用vcd包中提供的kappa()函数计算混淆矩阵的Cohen’s kappa值以及加权的 kappa 值。（举例来说，混淆矩阵可以表示两位评判者对于一系列对象进行分类所得结果的一致程度。）